
1. Allgemeines zu Geld und der Zinsrechnung
Auf der Welt dreht sich immer mehr alles um Geld. Das zeigt sich augenscheinlich darin, dass es immer mehr Reiche gibt und dass Reiche immer reicher werden. Dies ist eindeutig ein Ausdruck eines immer dominanter werdenden Kapitalismus. Das ist aber alles andere als schön, da hiermit auch eine immer größere Ungerechtigkeit einhergeht. Schließlich geht ein Anwachsen von Geld bei Privatpersonen stets nur auf Kosten einer Vielzahl an anderen Menschen. Das ist die bittere Wahrheit des Kapitalismus. Der Geldfluss geht bei einem ungezügelten Kapitalismus nämlich stets vermehrt in eine Richtung – in die Richtung der Kapitalisten bzw. Reichen.
Unabhängig von der globalen Kapitalentwicklung der Welt hat Geld aber auch etwas sehr Gutes. Jeder Warenwert kann in einen allgemeinen Geldwert umgerechnet werden. Dadurch hat man ein Zahlungsmittel mit dem man alles und jedes kaufen sowie gegen Geld alles und jedes verkaufen kann. Das macht das Leben unglaublich einfacher. Ansonsten müsste man stets dies und jenes gegen jenes und dies tauschen und das immer und immer wieder. So würde aber eine moderne Gesellschaft niemals funktionieren. Geld ist daher unstrittig eine große Errungenschaft unserer Zivilisation – aber bei einseitigem Kapitalfluss auch etwas hochgradig Verachtenswertes.
In der Schule kommt Geld bzw. der Geldwert neben dem Stoffgebiet Größen noch in einem weiteren um einiges wichtigerem Stoffgebiet vor: der Zinsrechnung. Geld hat ja bekanntlich die Eigenschaft, dass man es auf unterschiedlichste Weise vermehren kann. Eine Möglichkeit stellt hierbei eine Geldanlage bei eine Bank dar. Je nach Länge des dort deponierten Geldes erhält man dann Zinsen, da man hierfür von der Bank einen bestimmten Zinssatz garantiert bekommt.
2. Die Begriffe Kapital K, Zinsen Z und Zinssatz p %
Das Angenehme beim Zinsrechnen ist zunächst, dass die gleichen Rechnungen durchgeführt werden, wie es bei dem Prozentrechnen der Fall ist. Die Begriffe, um die sich das Zinsrechnen dreht, heißen zwar anders, sie entsprechen aber den Begriffen der Prozentrechnung.
Daher sollte man zunächst wissen, dass bei der Zinsrechnung:
das Kapital K dem Grundwert G entspricht,
die Zinsen Z dem Prozentwert W,
der Zinsatz p % dem Prozentsatz p %.
Hierbei ist anzumerken, dass eine genaue Entsprechung von Zinsen Z und Prozentwert W nur immer dann vorliegt, wenn die Zinsen sich auf 1 Jahr beziehen.
3. Die Formeln zur Berechnung des Kapitals K, der Zinsen Z und des Zinssatzes p %
Aufgrund des Bezugszeitraumes von einem Jahr lassen sich auch alle Formeln der Prozentrechnung 1 : 1 auf die Zinsrechnung übertragen. Natürlich stehen dann anstatt der Begriffe aus der Prozentrechnung die entsprechenden Begriffe aus der Zinsrechnung.
Das Kapital K kann daher stets folgendermaßen berechnet werden:
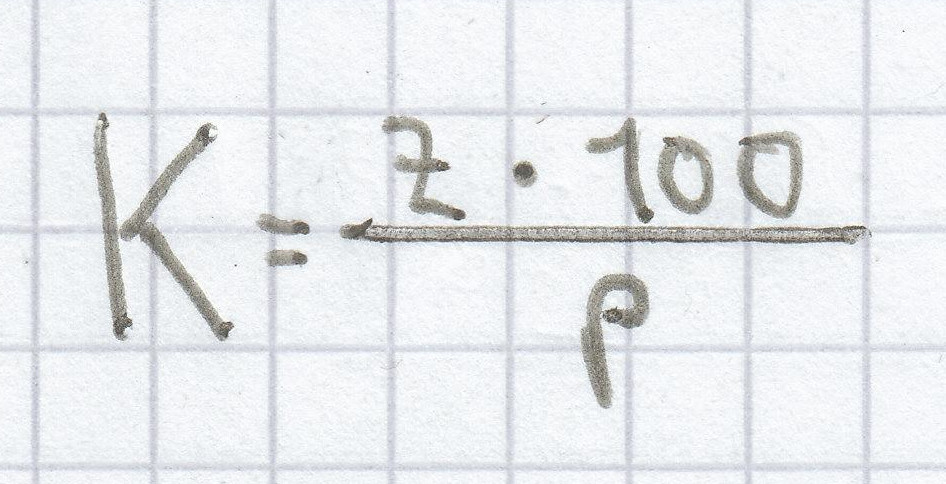
.
Beispiele:
Eine angelegte Geldsumme warf 72 Euro an Zinsen ab. Der Zinssatz belief sich hierbei auf 1,2 %. Wie viel Geld wurde angelegt?
Bezogen auf die Aufgabe ergibt sich:
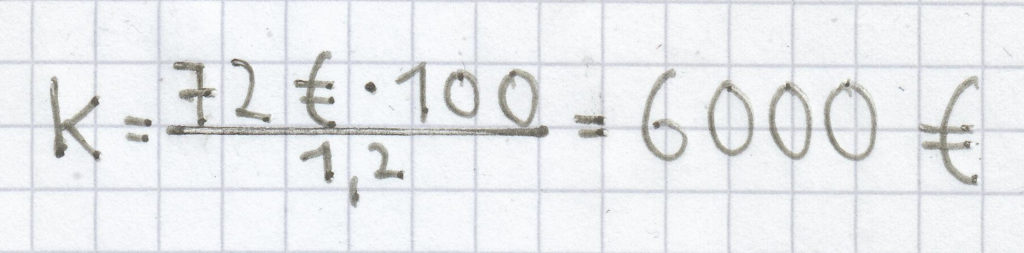
.
Es wurden 6000 Euro angelegt.
Eine Verzinsung von 1,4 % warf 56 Euro an Zinsen ab. Wie hoch war der angelegte Geldbetrag?
Bezogen auf die Aufgabe ergibt sich:
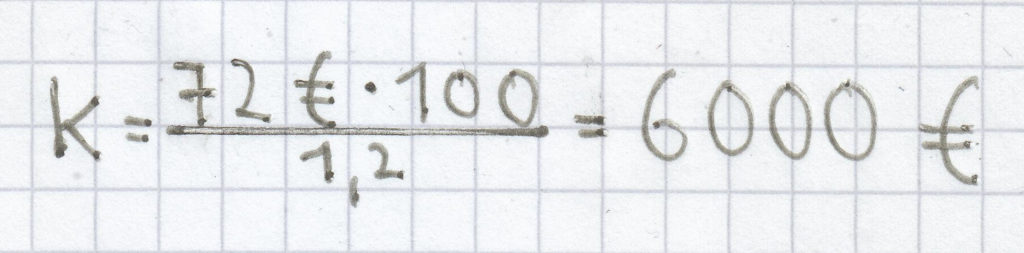
.
Der angelegte Geldbetrag betrug 4000 Euro.
Die Zinsen Z können stets auf diese Weise berechnet werden:
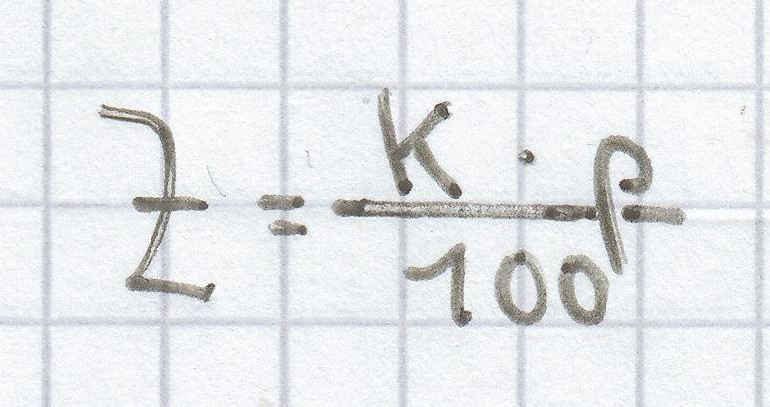
.
Beispiele:
Eine angelegte Geldsumme in Höhe von 6000 Euro wird zu 1,2 % verzinst. Wie hoche fallen die Zinsen aus?
Bezogen auf die Aufgabe ergibt sich:
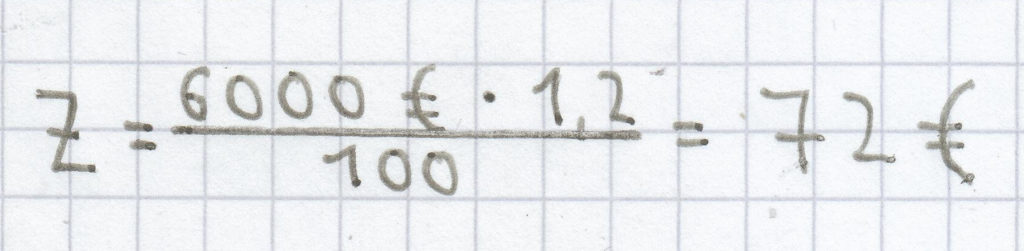
.
Es fallen 72 Euro an Zinsen an.
Ein Geldbetrag in Höhe von 4000 Euro wird zu 1,4 % verzinst. Wie viel an Zinsen sind das?
Bezogen auf die Aufgabe ergibt sich:
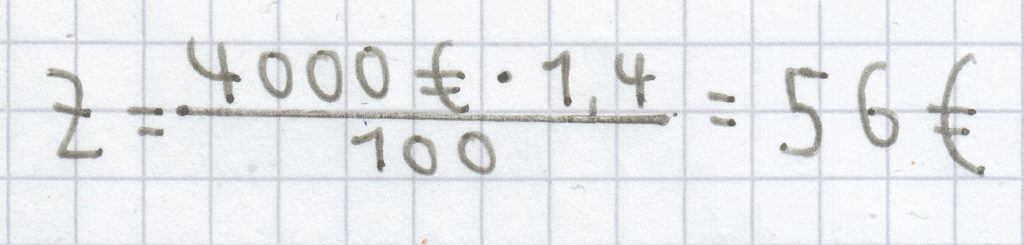
.
Das angelegte Geld wirft 56 Euro an Zinsen ab.
Der Zinssatz p % kann man stets mithilfe dieser Formel berechnen:
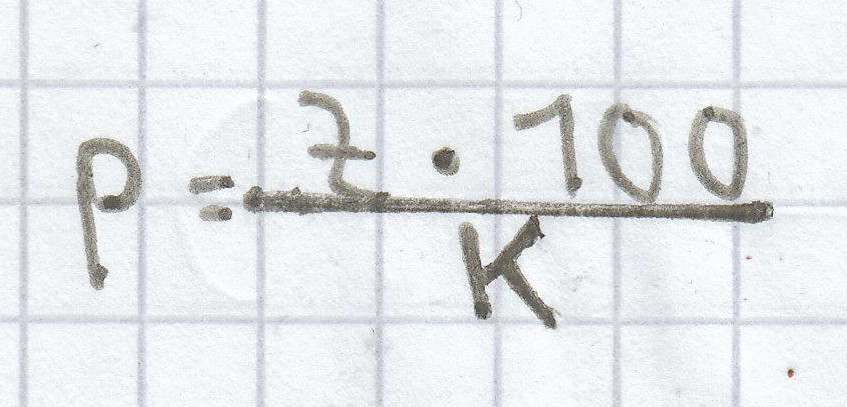
.
Beispiele: Ein angelegter Geldbetrag in Höhe von 6000 Euro warf 72 Euro an Zinsen ab. Wie hoch war der Zinssatz?
Bezogen auf die Aufgabe ergibt sich:
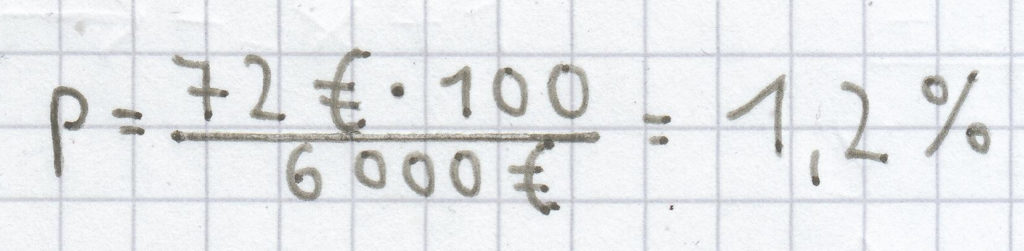
.
Der Zinssatz lag bei 1,2 %.
Es fielen bei einem Geldbetrag von 4000 Euro 56 Euro an Zinsen an. Welcher Zinssatz lag vor?
Bezogen auf die Aufgabe ergibt sich:
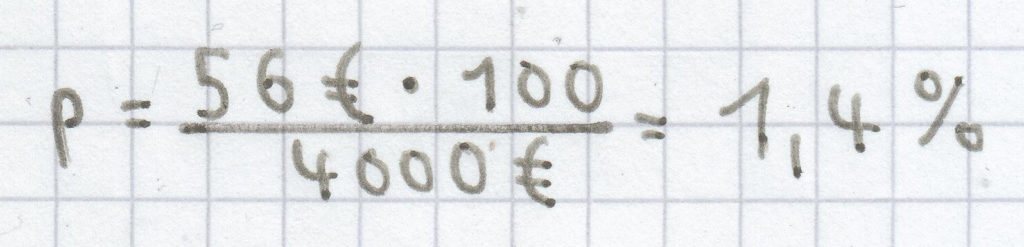
.
Der Zinssatz belief sich auf 1,4 %.
4. Wachstumsfaktor und Abnahmefaktor
Genauso wie bei der Prozentrechnung kann man auch bei der Zinsrechnung eine Zunahme des Kapitals K sofort berechnen, und zwar mit dem Wachstumsfaktor.
Den Wachstumsfaktor bei einer Zunahme des Kapitals K berechnet man dergestalt, wenn ein Zinssatz p % vorliegt:
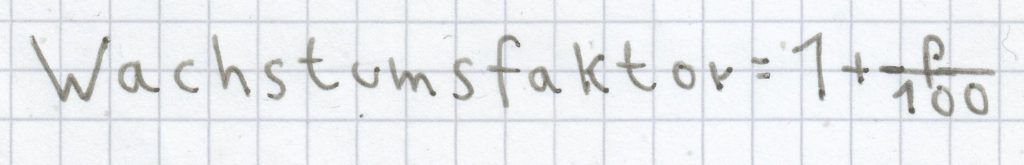
.
Eine Zunahme eines Kapitals K berechnet man nun folgendermaßen:
Wachstum = Kapital K · Wachstumsfaktor
.
Beispiel für eine Zunahme: Ein Betrag von 520 Euro wurde angelegt und wuchs um 5 % an. Wie hoch ist nun der jetzige Betrag?
Der Wachstumsfaktor berechnet sich wie folgt:
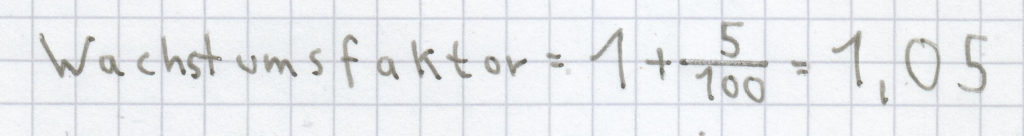
.
Die Zunahme ergibt sich mittels der Multiplikation des Kapitals K und des Wachstumsfaktors:
Zunahme = 520 € · 1,05 = 546 €.
Der angelegte Betrag ist nun auf 546 € angewachsen.
Beispiel für eine Zunahme: Stefan hat 5320 Euro bei einem Zinssatz von 1,5 % für ein Jahr angelegt. Wie hoch ist die Zunahme nach einem Jahr?
Der Wachstumsfaktor ist hier:
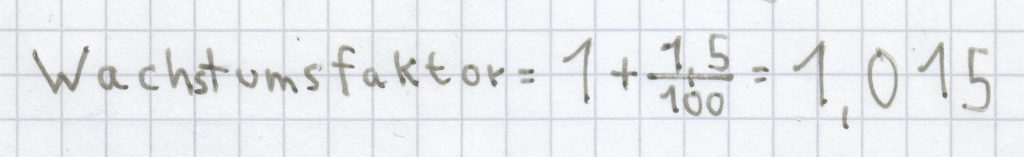
.
Die Zunahme kann man hier wiederum mittels der Multiplikation des Kapitals K und des Wachstumsfaktors ermitteln:
Zunahme = 5320 € · 1,015 = 5399,8 €.
Nach einem Jahr ist Stefans angelegtes Geld auf 5399,80 € angewachsen.
5. Die Formel der Zinsrechnung in Abhängigkeit zum Zeitfaktor
Bei sämtlichen obigen Formeln geht man davon aus, das der Zeitraum der jeweils gesuchten Begriffe Kapital, Zinsen und Zinssatz % stets ein Jahr umfasst. Nun gibt es aber auch gerade im Geldwesen andere Anlageformen, bei denen monatlich oder täglich Zinsen anfallen. Hierdurch ändert sich je nach Monatszinsen oder Tageszinsen die Formel zur Berechnung.
5.1 Die Berechnung von Monatszinsen und Tageszinsen
Die Formel zur Berechnung von Monatszinsen lautet dann:
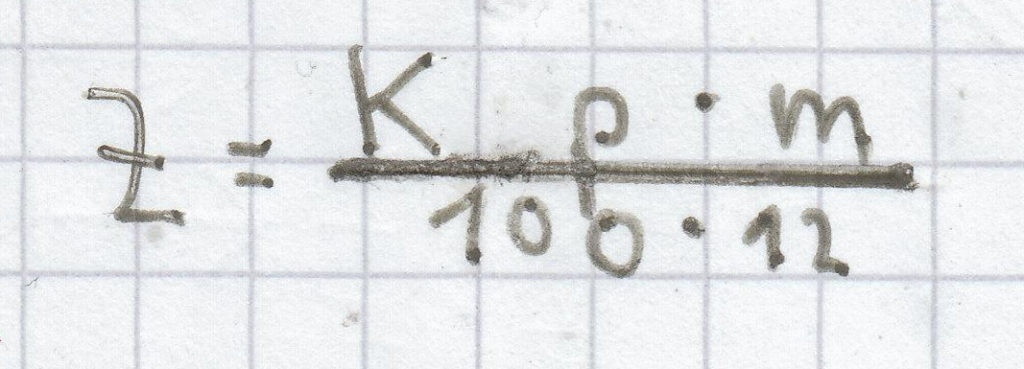
.
Die Formel zur Berechnung von Tageszinsen lautet dann:
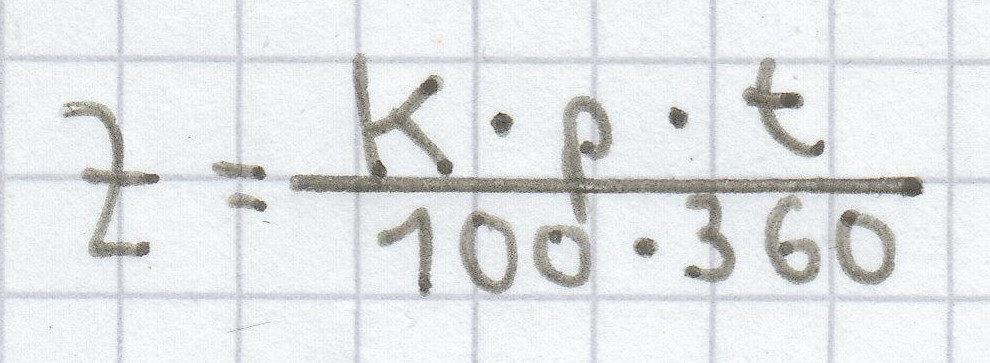
.
In der Zinsrechnung hat jeder Monat 30 Tage und somit ein Jahr insgesamt 360 Tage. Ein Zinsmonat umfasst daher 30 Zinstage, ein Zinsjahr 360 Zinstage.
Beispiel zur Berechnung von Monatszinsen
Herr Kaiser legt 4500 Euro über 7 Monate zu einem Zinsatz von 2,5 % an. Wie viel an Zinsen erhält er?
Eingesetzt in die Formel zur Monatszinsberechnung ergibt sich:
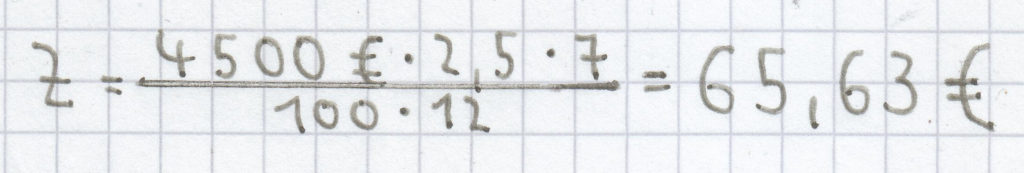
(gerundet auf zwei Nachkommastellen).
Herr Kaiser erhält nach 7 Monaten 65,63 € an Zinsen.
Beispiel zur Berechnung von Monatszinsen:
Frau Sommer möchte über einen Zeitraum von 8 Monaten 6500 Euro zu einem Zinssatz von 2 % anlegen. Wie viel an Zinsen erhält sie hierfür?
Eingesetzt in die Formel zur Berechnung der Monatszinsen ergibt sich:
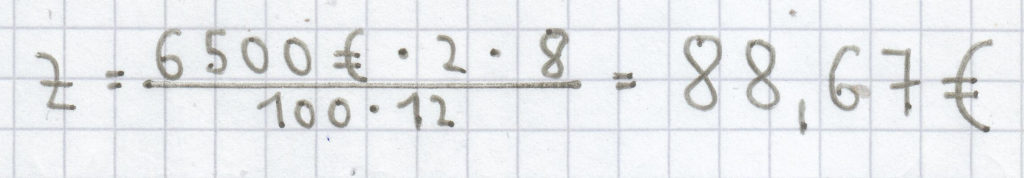
(gerundet auf zwei Nachkommastellen).
Frau Sommer würde nach 8 Monaten 86,67 € an Zinsen erhalten.
Beispiel zur Berechnung von Tageszinsen:
Ein Sparer legt 2560 € zu einem Zinssatz von 2 % 140 Tage lang an. Wie viele Zinsen fallen während dieses Zeitraums an?
Eingesetzt in die Formel zur Berechnung der Tageszinsen ergibt sich:
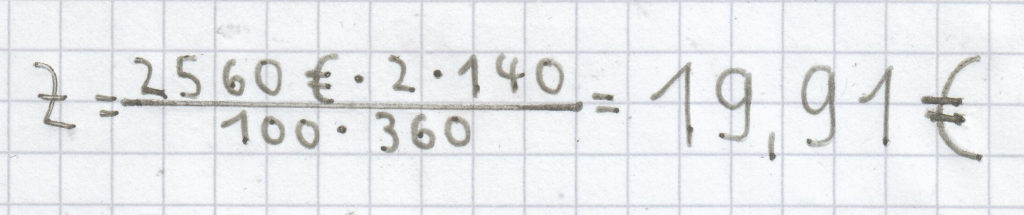
(gerundet auf zwei Nachkommastellen).
Der Sparer bekommt nach 140 Tagen für sein angelegtes Geld 19,91 € an Zinsen.
Beispiel zur Berechnung von Tageszinsen:
Ein Tagesgeldkonto bietet eine Verzinsung von 1,5 %. Wie viele Zinsen fallen nach 88 Tagen an, wenn man dort einen Betrag von 3210 Euro anlegt?
Eingesetzt in die Gleichung zur Berechnung der Tageszinsen ergibt sich:
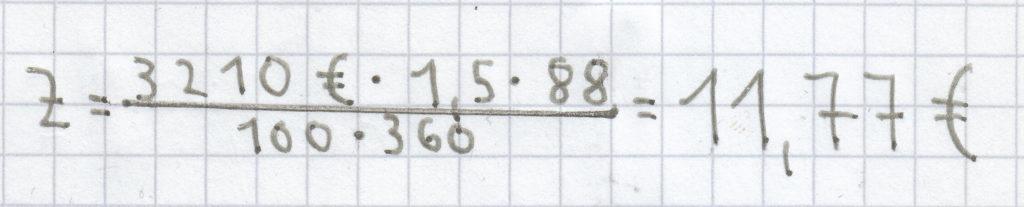
.
Nach 88 Tagen fallen für den angelegten Betrag 11,77 € an Zinsen an.
5.2 Die Berechnung von Monatszinsen und Tageszinsen mittels des Zeitfaktors i
Beide Formeln zur Berechnung von Monats- und Tageszinsen können auch mittels des sogenannten Zeitfaktors i zusammengefasst wiedergegeben werden.
Z = K · p · i
Der Zeitfakor i ist nichts anderes als der Quotient aus Monatsanzahl geteilt durch 12:
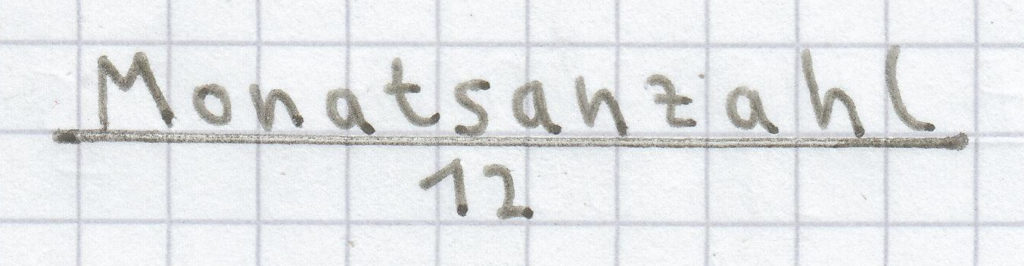
oder der Tagesanzahl geteilt durch 360:
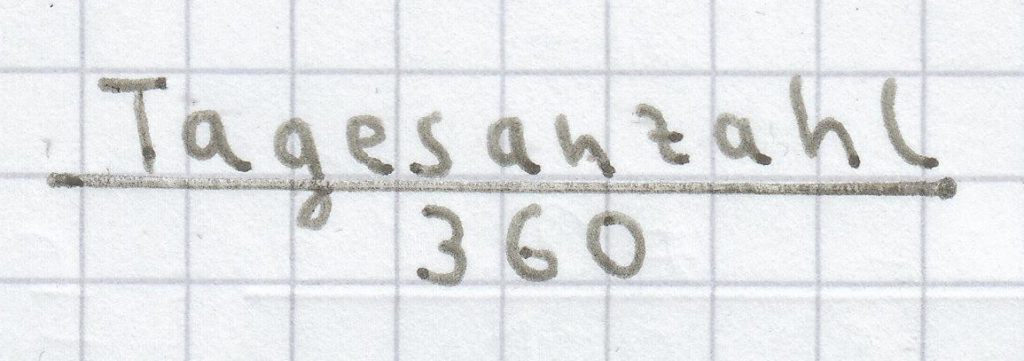
.
Beispiel zur Berechnung des Zeifaktors bei Monaten:
Ein Geldanlage soll 3 Monate angelegt werden. Berechne den Zinsfaktor.
Der Zeitfaktor ergibt sich mittels dieser Formel:
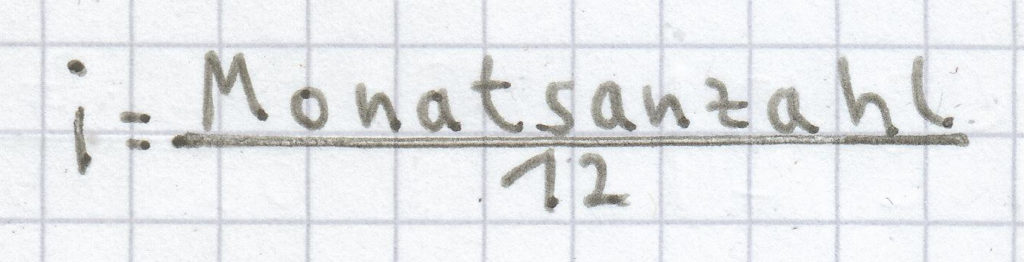
, eingesetzt ergibt sich hier:
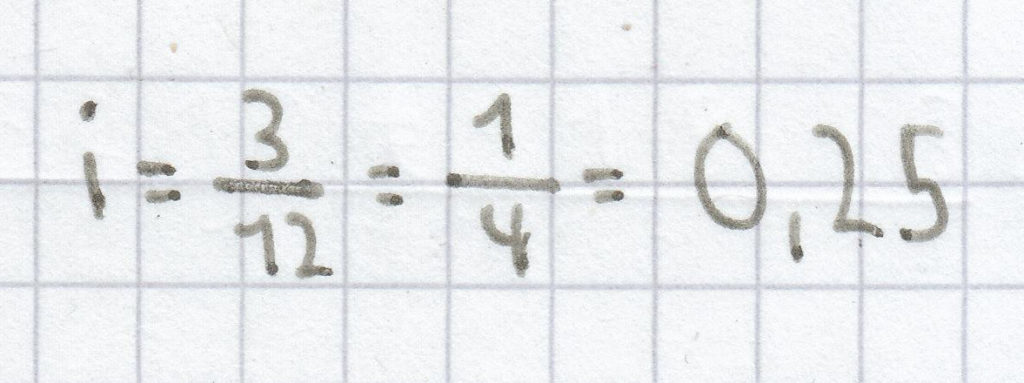
.
Der Zeitfaktor i beträgt hier 0,25.
Beispiel zur Berechnung des Zeitfaktors bei Tagen:
Eine Geldanlage soll 36 Tage lang angelegt werden. Berechne den Zeitfaktor.
Der Zeitfaktor kann man hier mittels dieser Formel ermitteln:
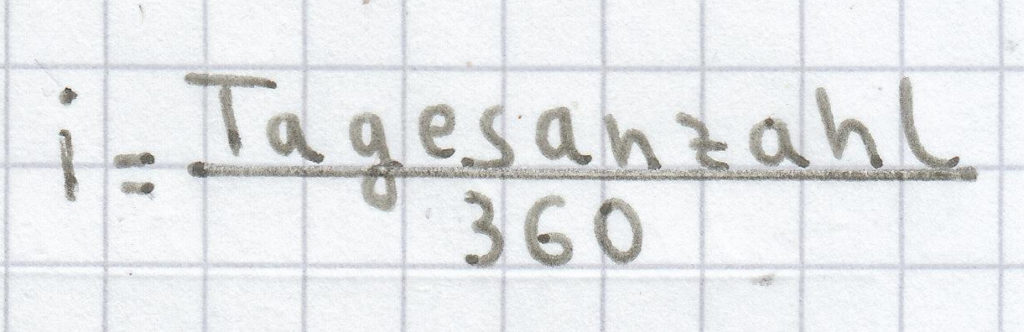
, eingesetzt ergibt sich:
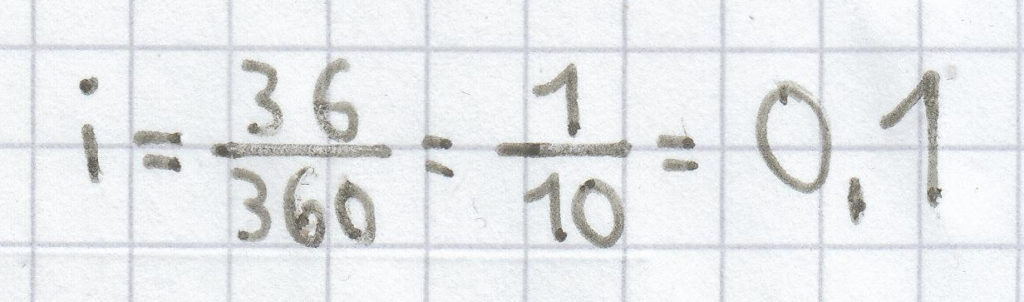
.
Der Zeitfaktor ist hier 0,1.
5.21 Der Zeitfaktor i bei einem Zeitraum von Tagen und/oder Monaten
Bei der Zinsrechnung kann es auch vorkommen, dass Zinsen über einen bestimmten Zeitraum von Tagen und/oder Monaten berechnet werden müssen. Hierzu verwendet man normalerweise ebenso den Zeitfaktor i. Im Bankwesen gilt hierbei: Der Einzahlungstag wird bei der Berechnung der Zinsen nicht mitgerechnet. Ferner gilt, wie oben bereits dargelegt: Ein Monat umfasst 30 Tage und ein Jahr 360 Tage.
Bei einem bestimmten Zeitraum, bei dem Zinsen anfallen, ermittelt man alle einzelnen Tage über eine Subtraktion. Hierbei schreibt man den Tag und den Monat des Zinsertragendes ganz oben und darunter immer den Tag und den Monat des Zinsertraganfangs.
Beispiel zur Berechnung des Zeitfaktors bei einem Intervall von Tagen und Monaten
Ein Anlagebetrag wird vom 16.2. bis zum 24.4. angelegt.
Durch Subtraktion ermittelt man hier zunächst die Tage und Monate, für die man Zinsen erhält:
24 Tage 4 Monate
– 16 Tage 2 Monate
______________________
8 Tage 2 Monate
= 8 Tage + 2 · 30 Tage = 68 Tage
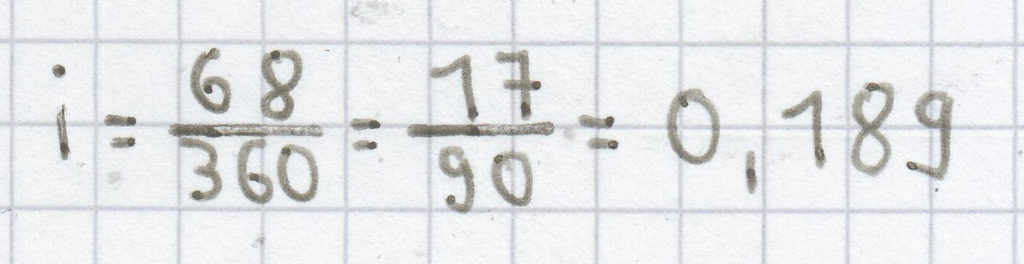
(gerundet auf die 3. Nachkommastelle).
Ist bei einem Zeitraum von Tagen und Monaten der Tag, an dem das Geld angelegt wird, höher (von der Zahl her) als der Tag, an dem die Geldanlage endet, so muss man Folgendes beachten: Damit die Subtraktion ein positives Ergebnis liefert, ist es notwendig einen Anlagemonat zu 30 Tage hin umzuwandeln und die 30 Tage hin mittels Addition zu dem Endtag der Geldanlage dazuzurechnen.
Beispiel zur Berechnung des Zeitfaktors bei einem Zeitraum von Tagen und Monaten
Ein Anlagebetrag wird vom 20.4. bis zum 16.6. angelegt.
Den 16.6. wandelt man um zum 46.5. (eine Monat löst man hin zu 30 Tagen auf).
16.6.: 46 Tage 5 Monate
20.4.: – 20 Tage 4 Monate
_________________________
26 Tage 1 Monat
= 26 Tage + 1 · 30 Tage = 56 Tage

(gerundet auf die 3. Nachkommastelle).
6. Die Berechnung von Zinseszinsen
Häufig legt man Geld deshalb an, damit die jährlich ausgeschütteten Zinsen mit dem angelegten Geldbetrag im Folgejahr mitverzinst werden – und im darauffolgenden Jahr wieder und dem darauffolgenden Jahr erneut… Dadurch wächst das über einen bestimmten längeren Zeitraum angelegte Geld entschieden schneller an, da hier dann ein sogenannter Zinseszins-Effekt vorliegt. Bei dem Zinseszins-Effekt liegt nämlich ein expotentielles Wachstum vor – was auch bei der Berechnungsformel des Zinseszins zum Ausdruck kommt.
Die Formel zur Berechnung des Zinseszins ist hierbei folgende:
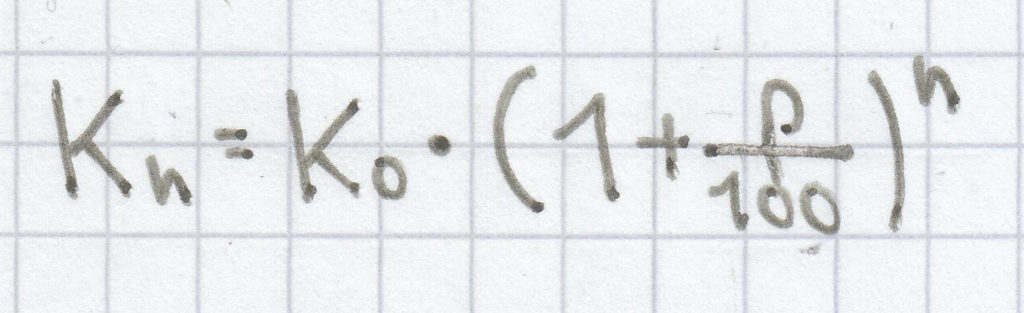
Die Formel zur Berechnung des Zinseszins setzt sich hierbei aus dem Zinsfaktor q zusammen, der nichts anderes als der Wachstumsfaktor ist:
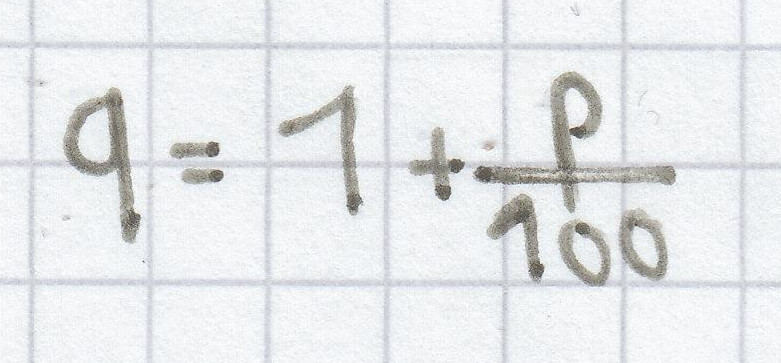
.
Die Anlagedauer wird hier mit n-Jahren wiedergegeben und der angelegte Grundbetrag mit K0., der angewachsene Betrag mit Kn.
Beispiel:
Acht Jahre lang wird ein Betrag von 1500 € zu einem Zinssatz von 3 % angelegt. Auf welchen Betrag ist das angelegte Geld nach dieser Zeit angewachsen?
n = 8; K0 = 1500 €; p % = 3 %
Eingesetzt in die Zinseszinsformel ergibt sich hier:
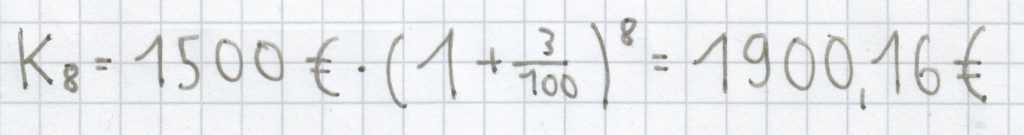
(gerundet auf zwei Nachkommastellen).
Nach acht Jahren ist der angelegte Geldbetrag auf 1900,16 € angewachsen.