1. Das Wurzelziehen als Gegenrechenoperation des Potenzierens
Zum Addieren gibt es in Mathe bekanntermaßen die Gegenrechenoperation, das Subtrahieren. Das Gleiche gilt für das Multiplizieren, denn hier kennt auch jeder die Gegenrechenoperation: das Dividieren. Wie sieht das nun beim Potenzieren aus? Richtig! Jeder in Mathematik nicht gänzlich auf den Kopf gefallene Schüler weiß auch, dass es hierfür eine Gegenrechenoperation gibt. Egal, ob man den Namen hierfür kennt oder nicht – gemeint ist hier: das Radizieren bzw. auf Deutsch: das Wurzelziehen.
Da eine Wurzel immer auf eine Potenz zurückgeführt werden kann, lässt sich diese neue Rechenoperation, das Radizieren/Wurzelziehen am besten aufgrund des Beziehungsverhältnisses Potenz/Wurzel erklären.
Gegeben ist folgende Potenz: 43
Die diesen Wert hat: 43 = 4 ∙ 4 ∙ 4 = 64
Die Gegenrechenoperation ist nun hier:
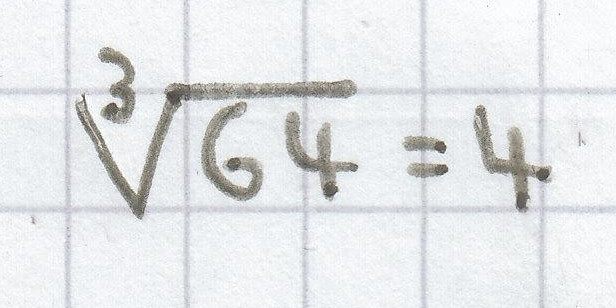
Bei einer Variablen/Zahl unter einer Potenz und dem Ergebnis a besteht folgende Wechselbeziehung bzw. die Möglichkeit dieser Gegenrechenoperation (veranschaulicht auf beiden Bildern).
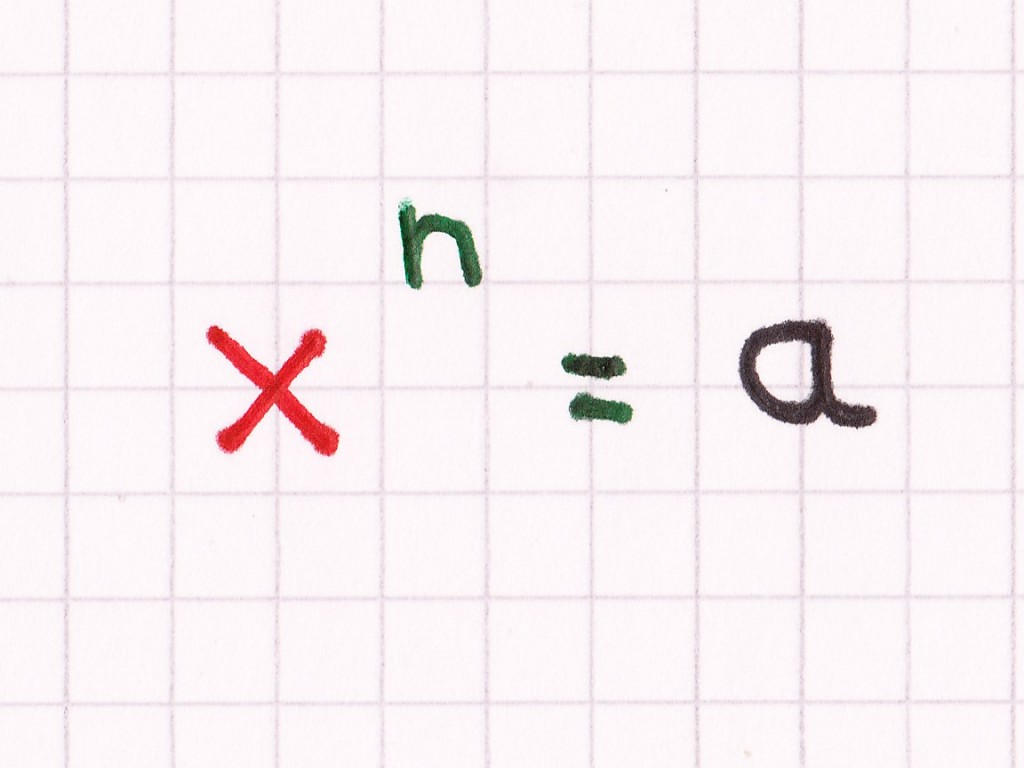
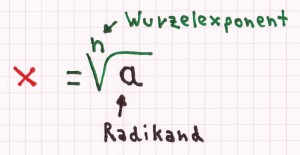
Durch das Ziehen der n-ten Wurzel von a erhält man x.
Aus dieser Beziehung zwischen Potenz und Wurzel ergibt sich folgende Definition:
Es ist eine nichtnegative Zahl a gegeben (alle Zahlen größer 0).
Die n-te Wurzel (n ≥ 2) ist diejenige nichtnegative Zahl x, aus der man mit n potenziert die Zahl a erhält.
Die n-te Wurzel aus a in der Sprache der Mathematik hat die Form:

.
Die Zahl n nennt man Wurzelexponent, die unter dem Wurzelzeichen stehende Zahl a bezeichnet man als Radikand.
Beispiele:

, denn 8 ∙ 8 = 64 (gesprochen: die Wurzel aus 64, alternativ: die Quadratwurzel aus 64);
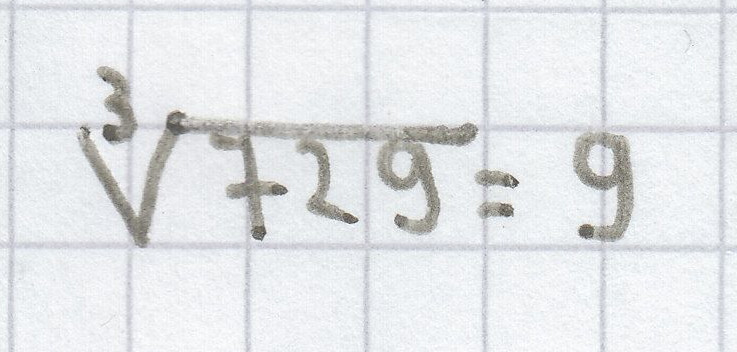
, denn 9 ∙ 9 ∙ 9 = 729 (gesprochen: die 3. Wurzel aus 729, alternativ: die Kubikwurzel aus 729);
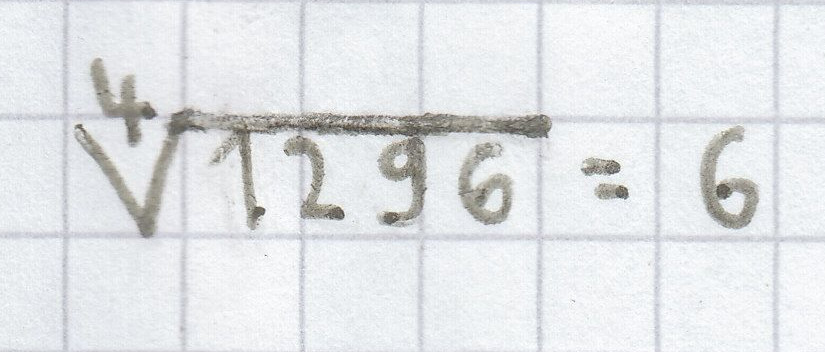
, denn 6 ∙ 6 ∙ 6 ∙ 6 = 1296 (gesprochen: die 4. Wurzel aus 1296);

, denn 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 243 (gesprochen: die 5. Wurzel aus 243).
Weist die Wurzel keinen Wurzelexponenten auf, so handelt es sich immer um eine Quadratwurzel:
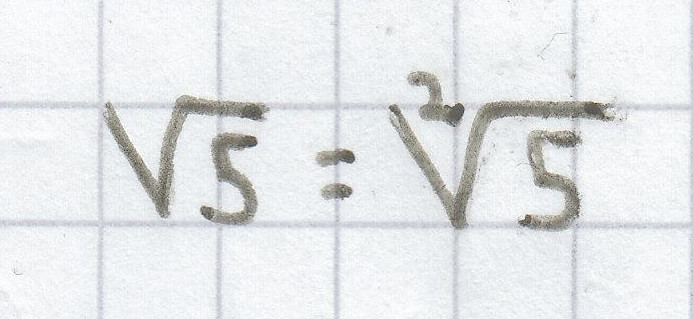
.
1.1 Berechnung der n-Wurzel mit dem Taschenrechner
Bei Taschenrechnern für den Mathematik-Unterricht kann man die n-te Wurzel immer mit dieser Taste berechnen:

. Normalerweise befindet sich diese Taste auf der 2. Belegung des Taschenrechners.
Bei Taschenrechnern, die die Taste

nicht vorweisen, kann man die n-te Wurzel aber auch folgendermaßen berechnen: Man gibt zuerst den Radikanden in den Taschenrechner ein und drückt als Nächstes die Taste xy. Darauf gibt man den Kehrwert des Wurzelexponenten ein – und das entweder als Bruch oder Dezimalzahl.
Beispiele:
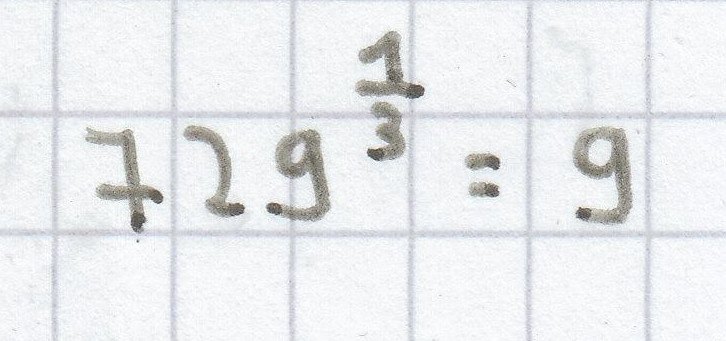
;
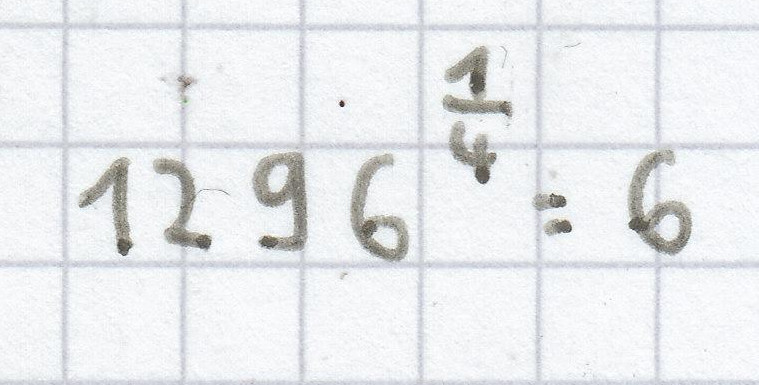
oder: 12960,25 = 6
;
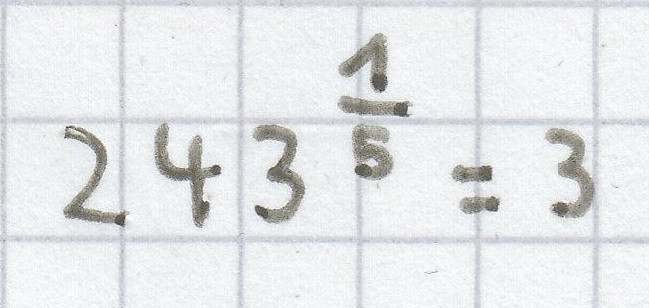
oder: 2430,2 = 3
Je nach Taschenrechner ist es wichtig, um den Exponenten eine Klammer zu setzen.
2. Die Wechselbeziehung zwischen Wurzelziehen und Potenzieren
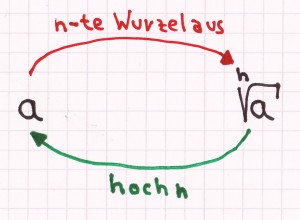
Das Ziehen der n-ten Wurzel wird durch die Gegenrechenoperation, durch das Potenzieren mit n, wieder aufgelöst beziehungsweise rückgängig gemacht.
Denn:
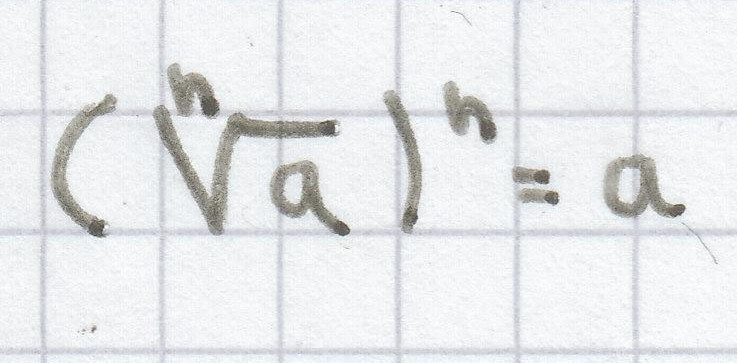
für a ≥ 0
Beispiele:
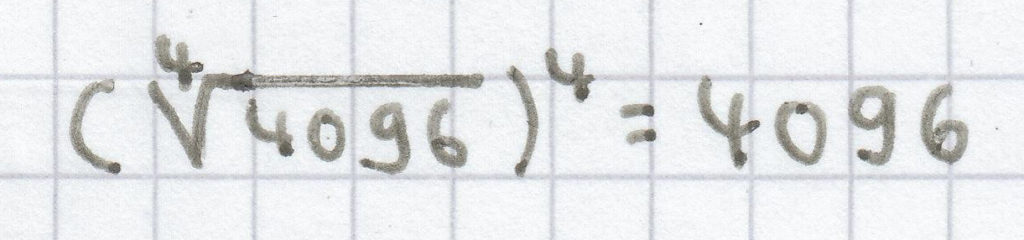
;
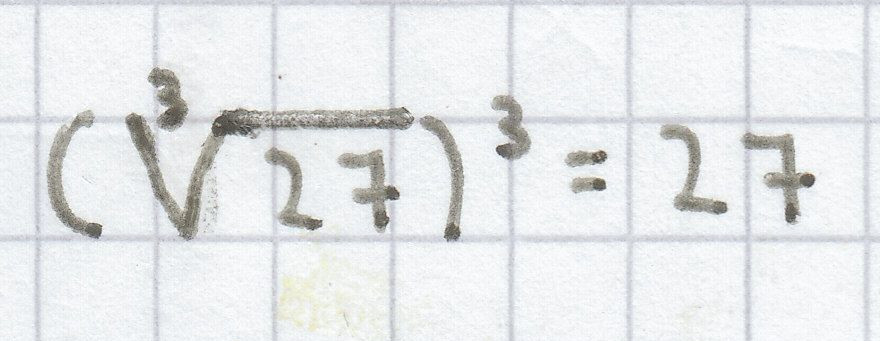
;
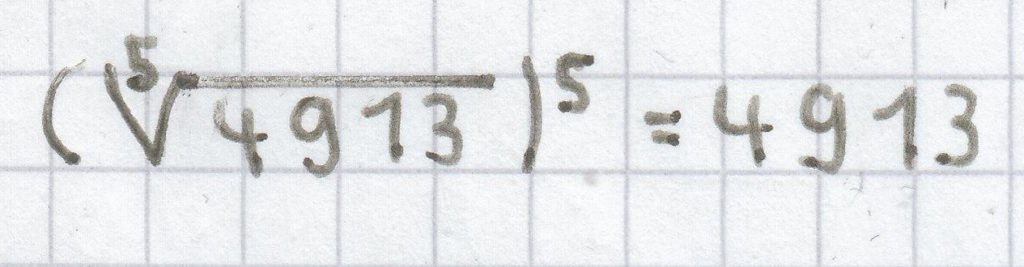
;
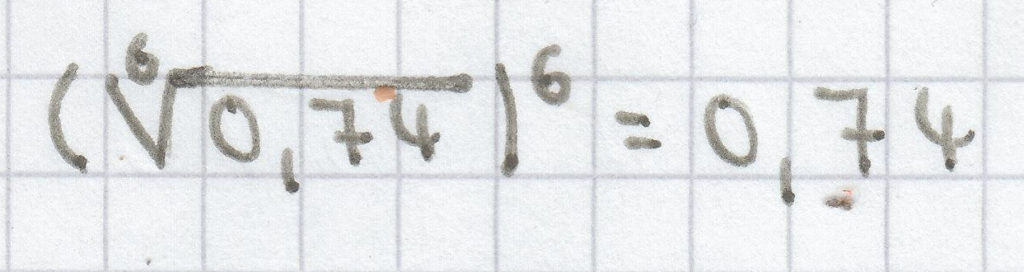
.
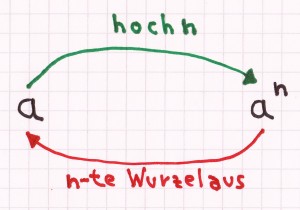
Das Potenzieren von n wird durch die Gegenrechenoperation, das Ziehen der n-ten Wurzel wieder aufgelöst beziehungsweise rückgängig gemacht.
Denn:
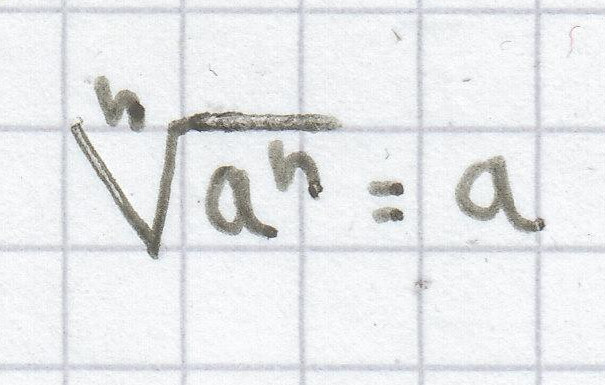
für a ≥ 0
Beispiele:

;
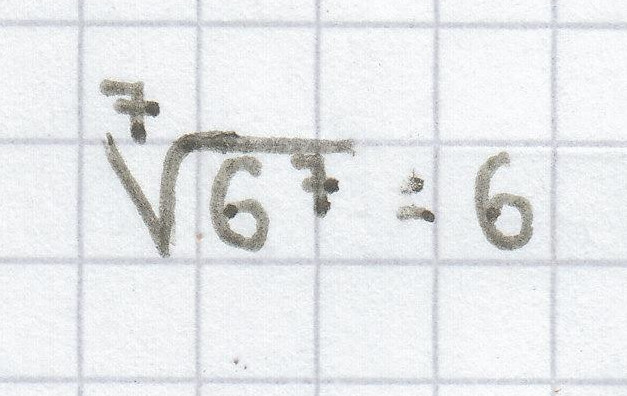
2.1 Die Lösungsmenge einer Gleichung der Form xn = a
Je nach Exponent in Beziehung zu a kann eine Gleichung der Form xn = a eine Lösung oder zwei Lösungen haben oder keine Lösung vorweisen.
Definition:
Für die Lösungsmenge der Gleichung xn = a gilt
bei geradem Exponenten n:
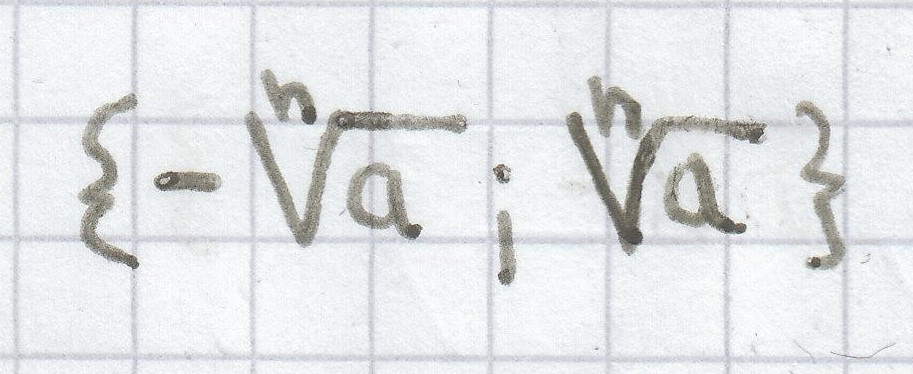
, wenn a > 0;
{0}
, wenn a = 0;
{ }
, wenn a < 0;
bei ungeradem Exponenten:

, wenn a > 0;
{0}
, wenn a = 0;
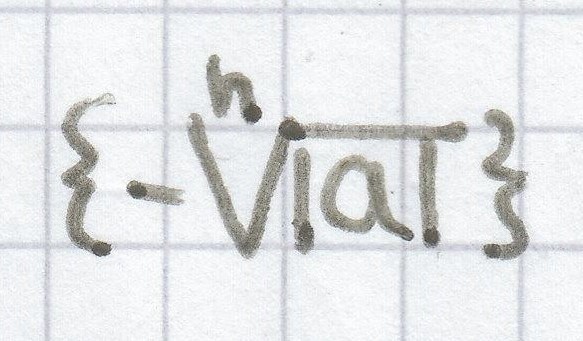
, wenn a < 0.
3. Die Erweiterung des Potenzbegriffs: auf gebrochen rationale Exponenten
Jede Wurzel kann auch als Potenz wiedergegeben werden. Hierfür ist nur eine Erweiterung des Potenz-Begriffes vonnöten, und zwar dahingehend, dass der Exponent der Potenz auch gebrochen rationale Zahlen beinhalten kann.
Definition:
Eine Potenz mit einem gebrochen rationalem Exponenten kann man zu einer Wurzel hin umwandeln.
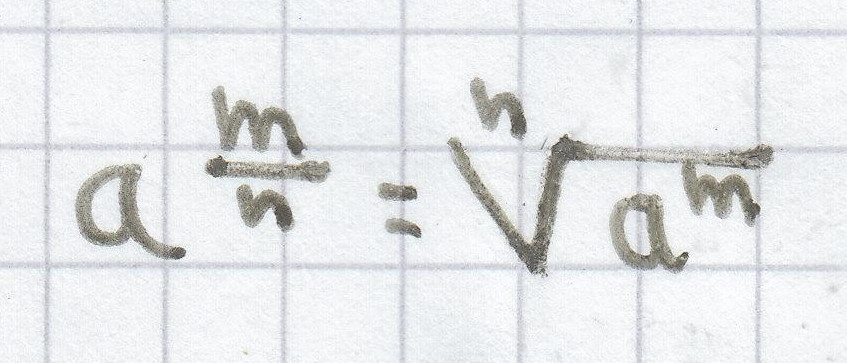
(für m Є , und n Є ℤ, n Є ℕ*}, a > 0)
Hierbei wird der Nenner des Bruchs zum Wurzelexponenten und der Zähler des Bruchs zum Exponenten des Radikanden.
Bei m = 1 tritt dieser Sonderfall auf:
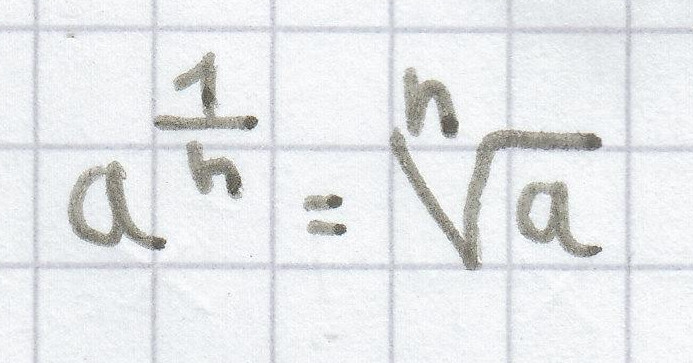
.
Beispiele:
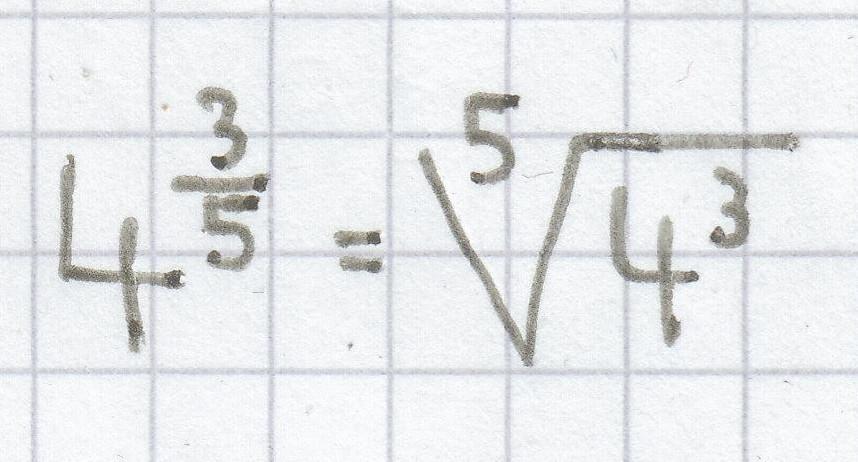
;
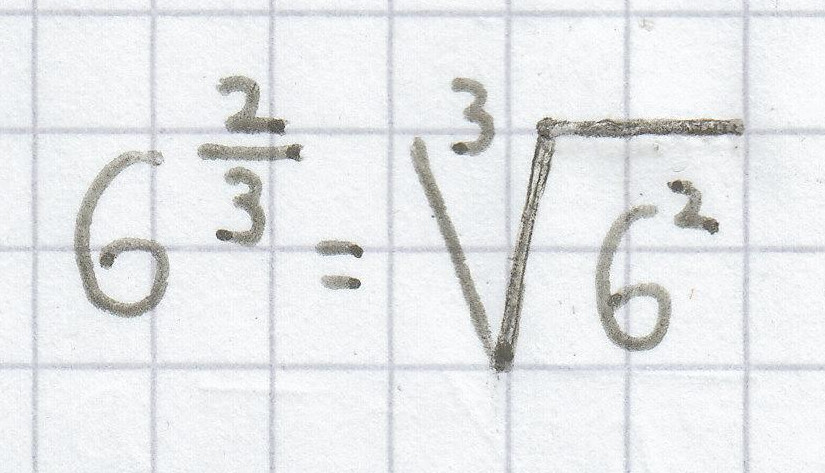
;
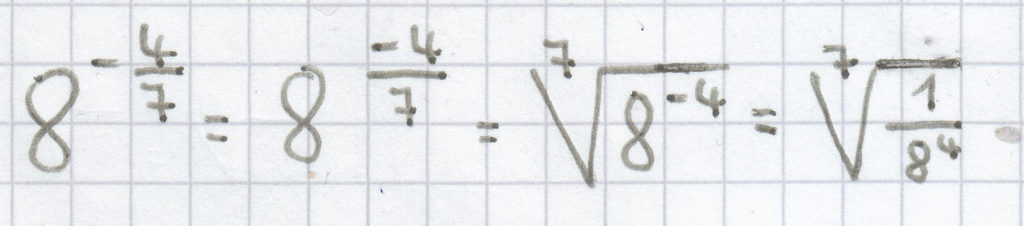
;
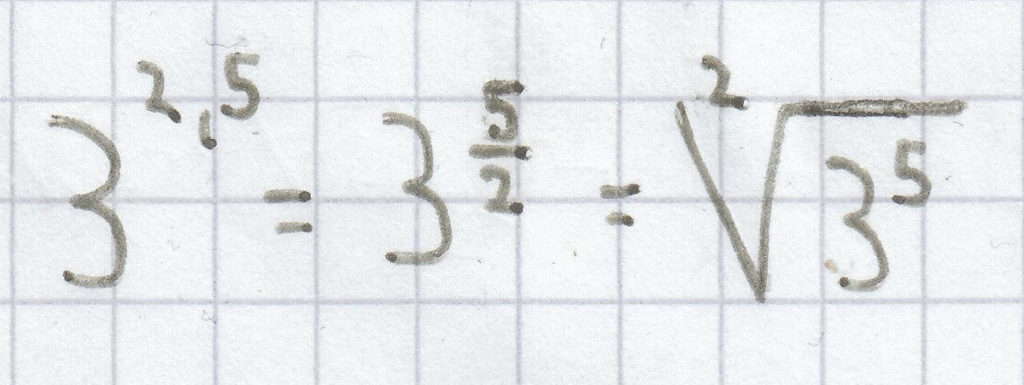
.
4. Wurzelgesetze
Genauso wie bei Potenzen gibt es in Mathe zu Wurzeln Rechenoperationen, die klaren Regeln unterliegen. Diese werden als Wurzelgesetze bezeichnet. Hierbei gibt es folgende Unterteilungen:
- Wurzelgesetz für die Multiplikation von Wurzeln mit gleichem Wurzelexponenten
- Wurzelgesetz für die Division von Wurzeln bei gleichem Wurzelexponenten
- Wurzelgesetz für das Wurzelziehen einer Wurzel
4.1 Wurzelgesetz für die Multiplikation von Wurzeln mit gleichem Wurzelexponenten
Liegt eine Multiplikation zweier Wurzeln mit gleichem Wurzelexponenten vor, so ergibt sich hieraus diese Gesetzmäßigkeit:
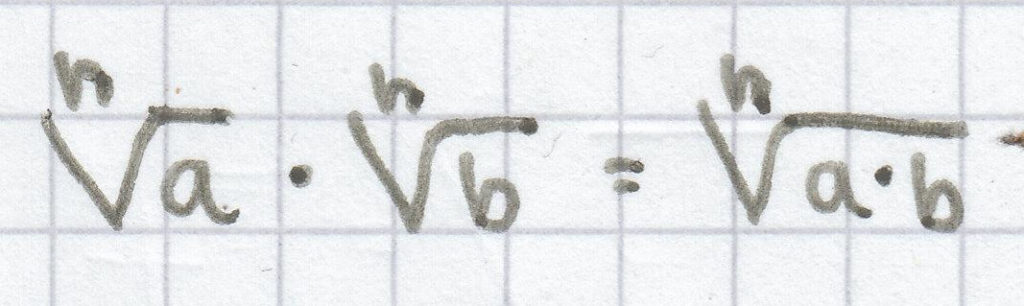
für a ≥ 0, b ≥ 0
Bei der Multiplikation zweier verschiedener Radikanden, deren Wurzelexponenten gleich sind, werden die Radikanden miteinander malgenommen. Der Wurzelexponent bleibt hierbei bestehen.
Beispiele:

;
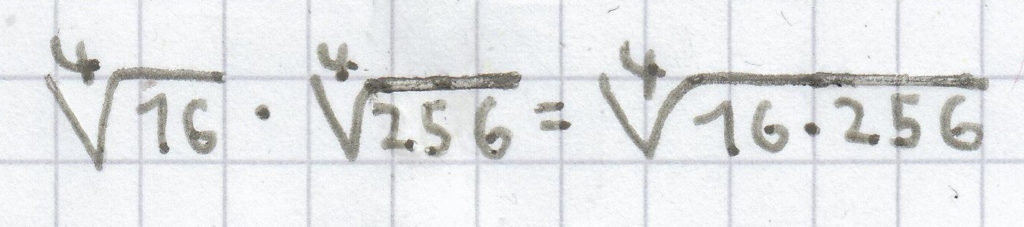
4.2 Wurzelgesetz für die Division von Wurzeln mit gleichem Wurzelexponenten
Bei einer Division zweier Wurzeln mit gleichem Wurzelexponenten ergibt sich folgende Gesetzmäßigkeit:
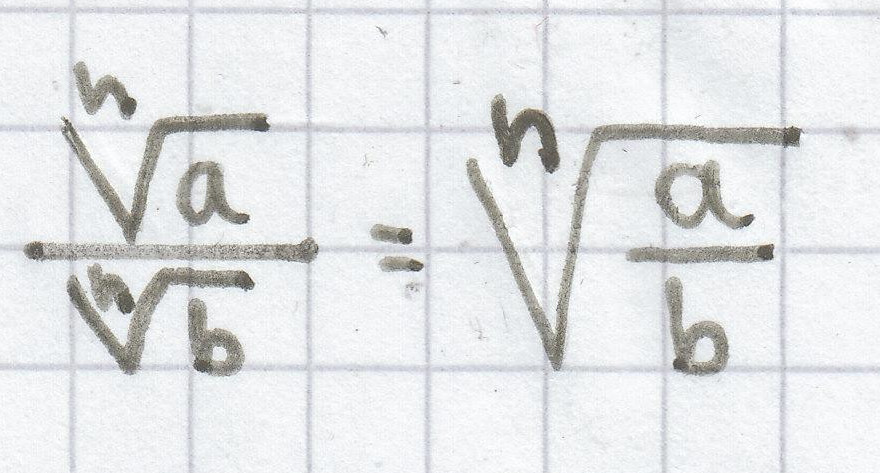
für a ≥ 0, b > 0
Bei der Division zweier verschiedener Radikanden, die den gleichen Wurzelexponenten vorweisen, wird der Quotient beider Radikanden genommen bzw. der zweite Radikand durch den ersten Radikanden dividiert. Der Wurzelexponent bleibt hierbei bestehen.
Beispiele:
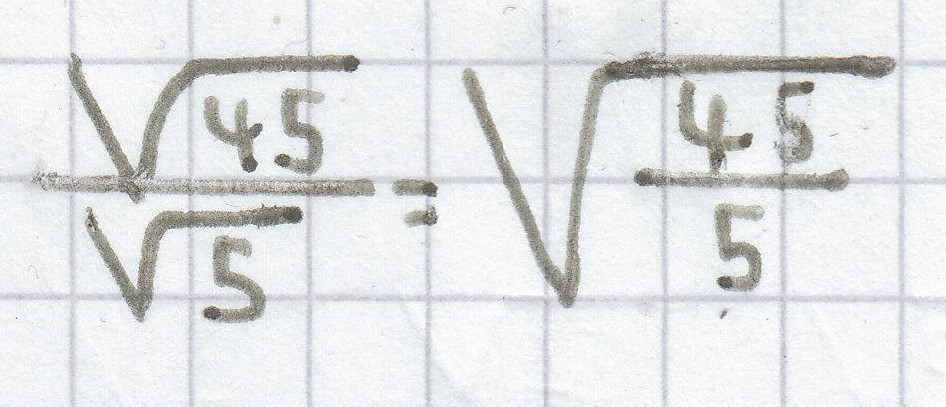
;
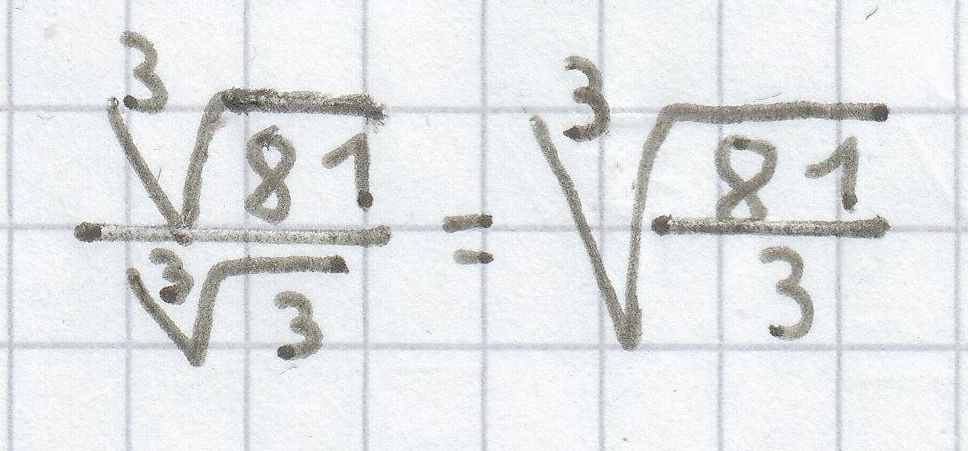
4.3 Wurzelgesetz für das Wurzelziehen aus einer Wurzel
Zieht man aus einer Wurzel die Wurzel, so liegt folgende Gesetzmäßigkeit vor:
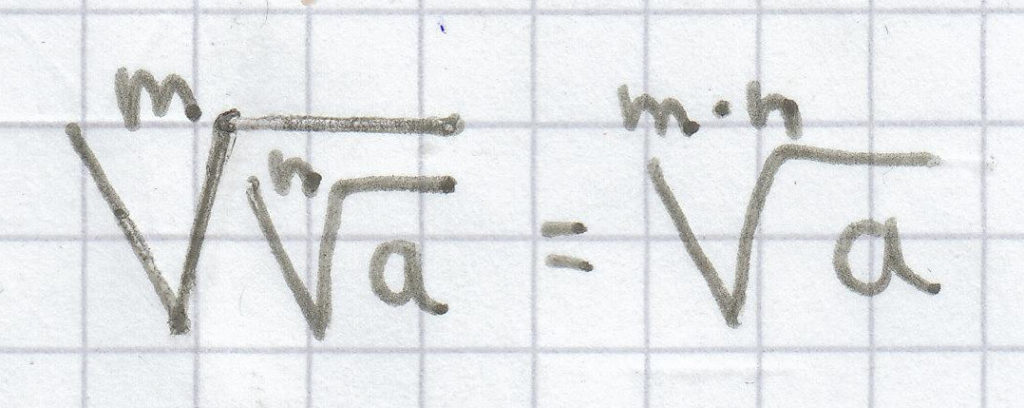
für a ≥ 0
Bei einer Wurzel zieht man die Wurzel, indem man die Wurzelexponenten miteinander multipliziert. Der Radikand der Wurzel bleibt hierbei erhalten.
Beispiele:
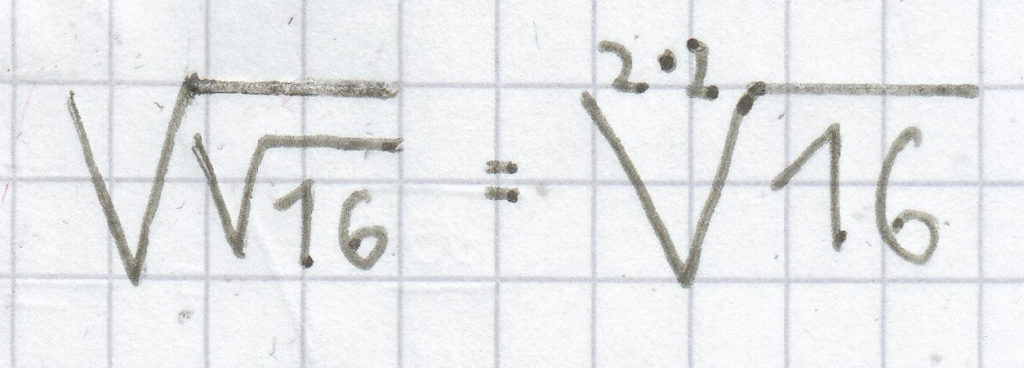
;
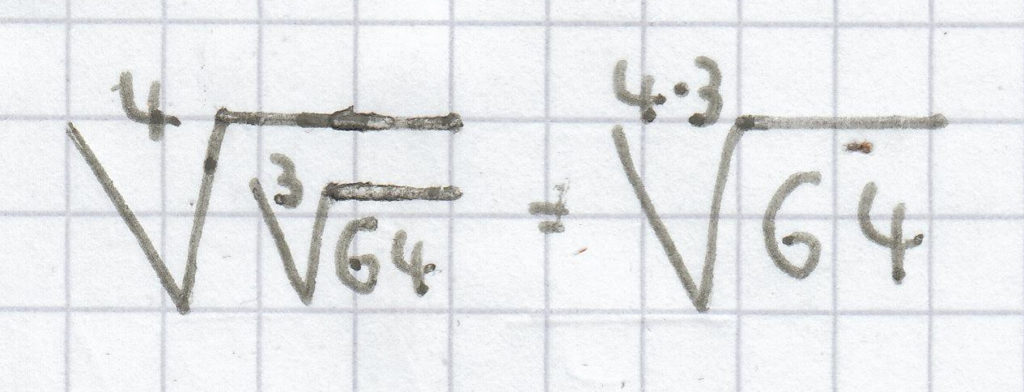
4.4 Sonderfälle von Wurzelgesetzen
Aus den obigen Wurzelgesetzen lassen sich folgende Sonderfälle an Wurzelgesetzen ableiten.
4.41 Das teilweise Wurzelziehen
1a)
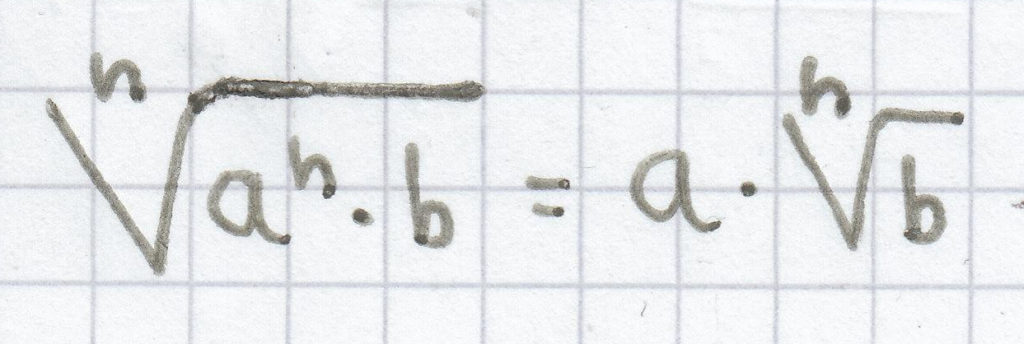
(für a ≥ 0, b ≥ 0)
Beispiele:
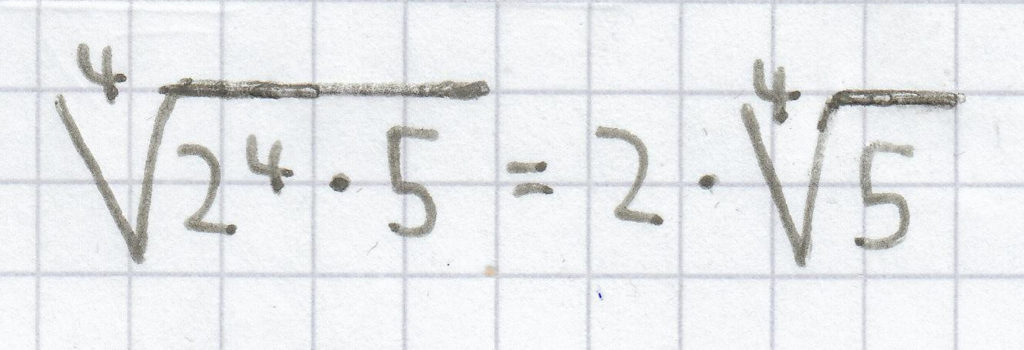
;
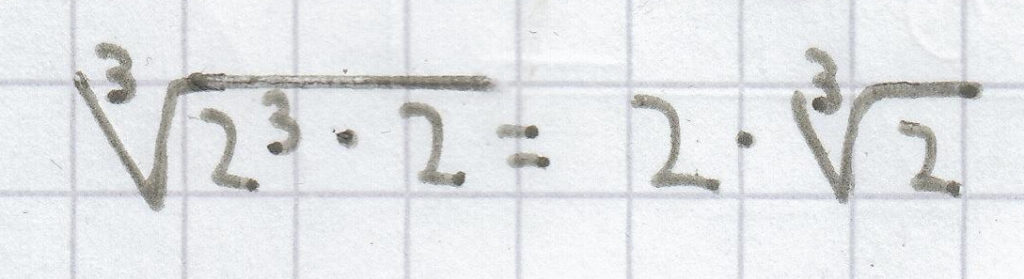
1b)
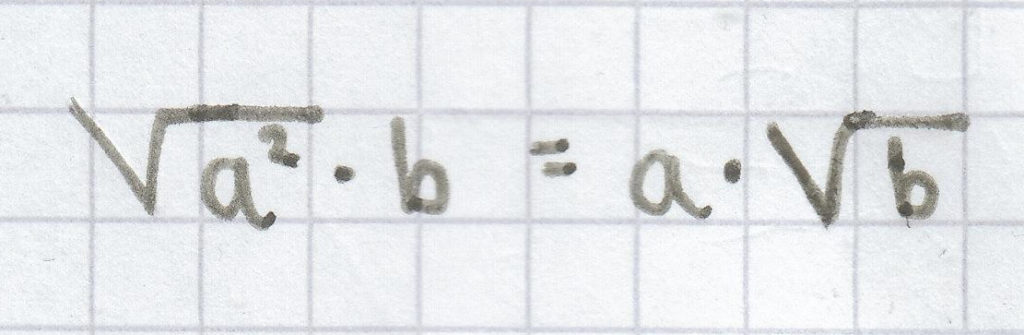
(für b ≥ 0)
Beispiele:
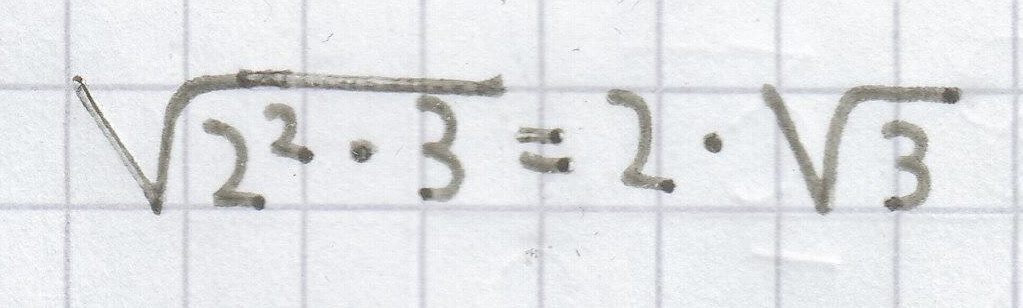
;

;

;
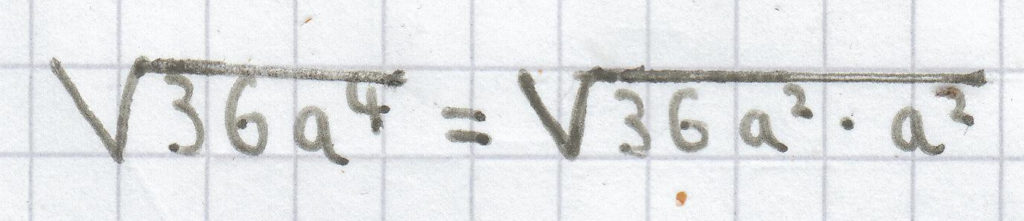
= 6 · a · a
;
2)
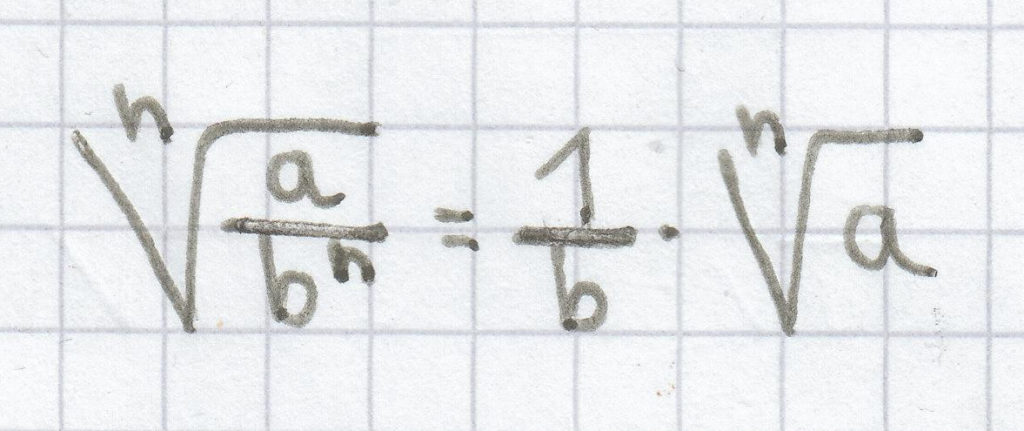
(für a ≥ 0, b > 0)
;
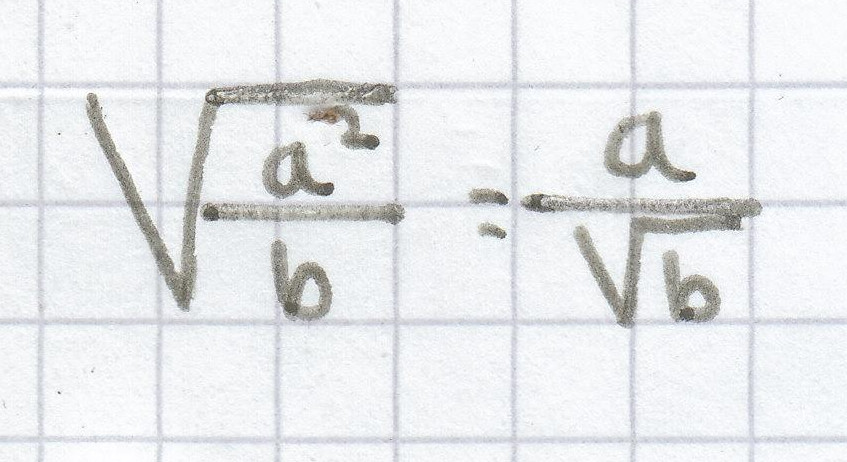
(für b > 0)
;
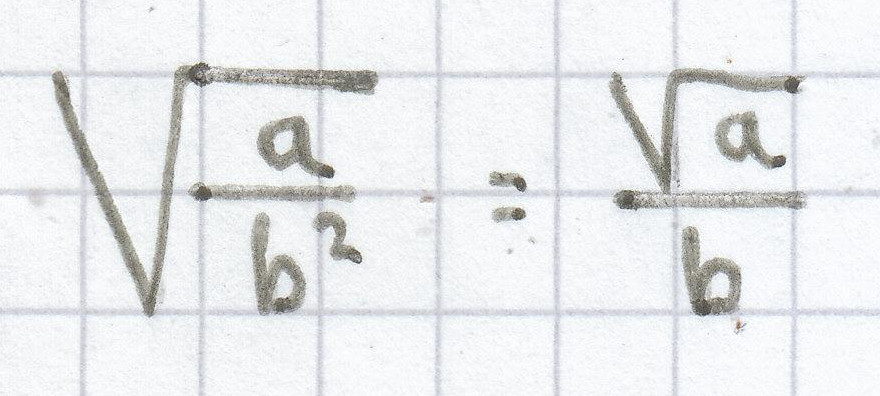
(für a ≥ 0, b ≠ 0)
;
3)
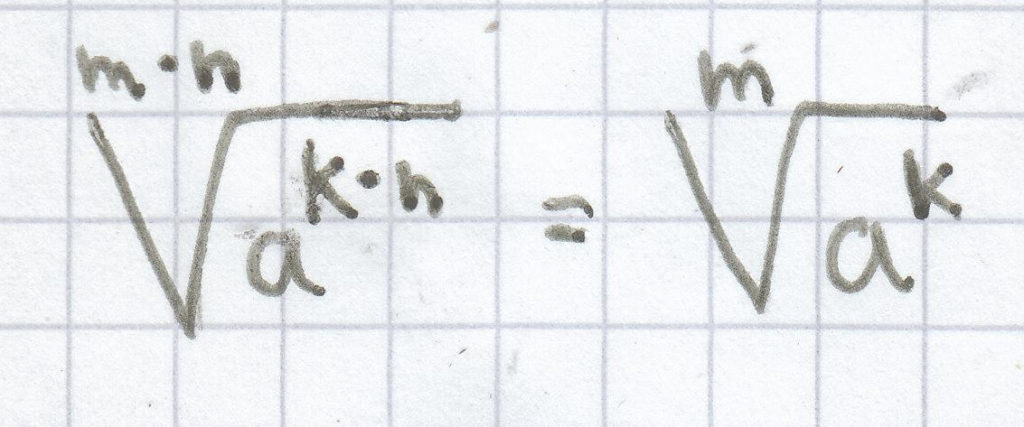
(für a ≥ 0, m ∈ ℕ, k ∈ ℕ, n ∈ ℕ)