
Ein nicht allzu schweres Mathe-Stoffgebiet stellt das Prozentrechnen dar. Schließlich basiert es zum einen nur auf der Multiplikation und Division, zum anderen dreht es sich stets um drei Begriffe – wobei der gesuchte Begriff stets mittels einer Mathematik-Formel berechnet werden kann. Daher ist das Prozentrechnen auch für Nicht-Mathe-Fans eine jederzeit zu bewältigende Hürde.
Die drei Begriffe, um die das Prozentrechnen kreist, sind hierbei der Grundwert G, der Prozentwert W und der Prozentsatz p %. Die drei Formeln zur Berechnung des jeweils gesuchten Begriffs setzen sich wie folgt zusammen:
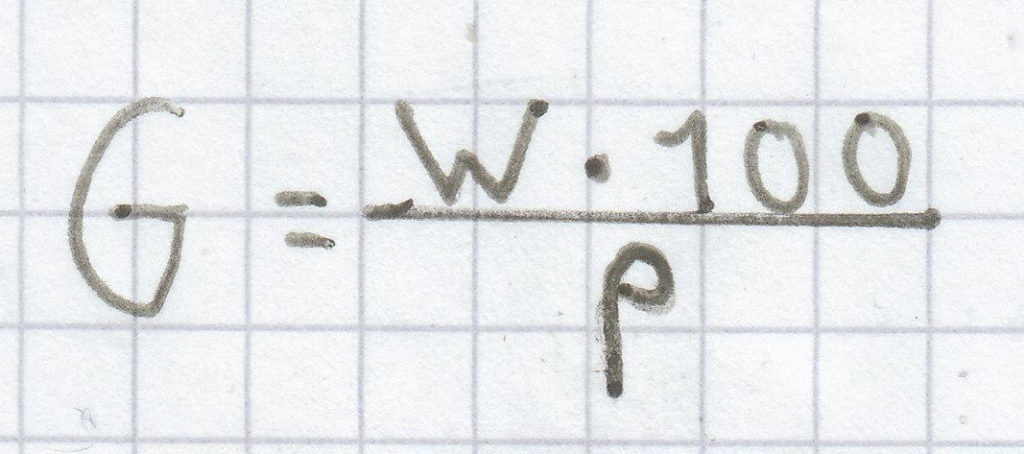
;
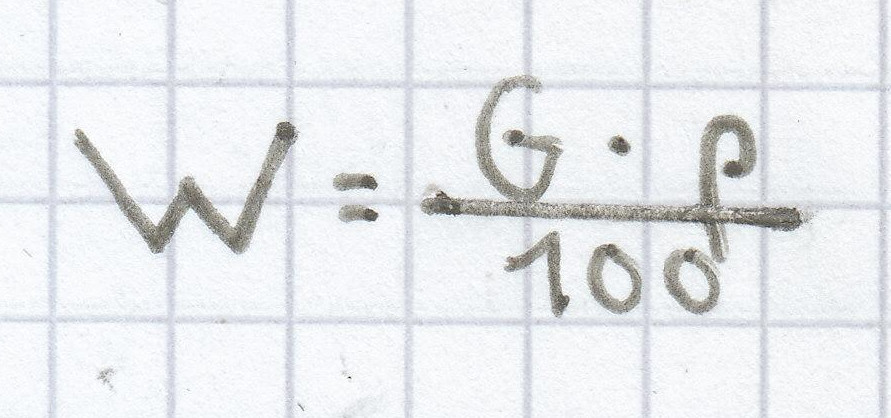
;
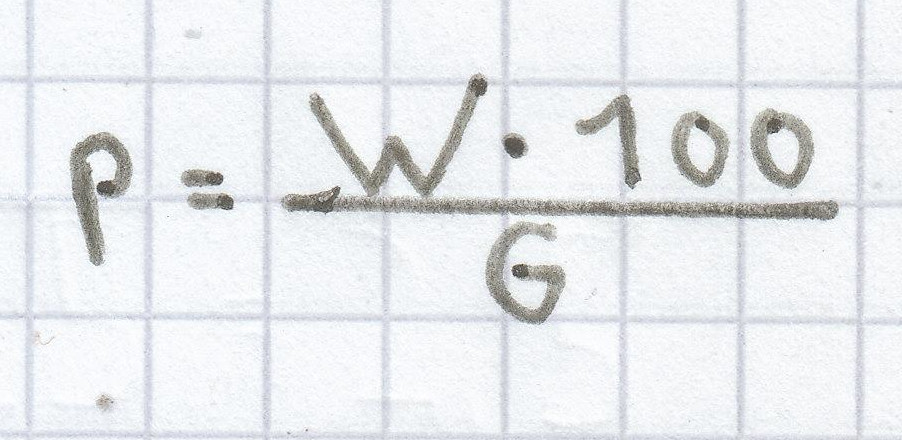

Bevor man eine der drei Formeln verwendet, sollte man immer ganz sicher sein, welcher Begriff auch wirklich gesucht ist.
Während der Mathematik-Arbeit muss man die Mathe-Formeln, die man bei dem Stoffgebiet Prozentrechnung stets benutzt, sogar auswendig können. Bei der MSA-Prüfung thematisiert mindestens immer eine Aufgabe das Prozentrechnen. In der hierfür extra bereitgestellten Formelsammlung sind diese aber alle enthalten – und das Langzeitgedächtnis wird somit nicht auch noch bei dieser Prüfung mit einem speziellen Prozentrechnungsformelwissen geplagt werden.
Aufgaben zum Mathematik-Stoffgebiet Prozentrechnung
1. Mathe-Nachhilfe-Aufgabe: Ermittle jeweils den Prozentwert.
a)
15 % von 200 €
80 % von 800 kg
5 % von 550 m²
20,5 % von 320 l
100 % von 322 cm
b)
4 % von 520 t
82 % von 240 €
15 % von 220 l
51 % von 820 kg
2 % von 350 m³
c)
15,4 % von 250 l
20,2 % von 140 €
82,5 % von 40 kg
8,5 % von 34 €
33,3% von 1200 m
2. Mathematik-Nachhilfe-Aufgabe: Ermittle den Prozentsatz.
a)
(p % von 120 €) = 63 €
(p % von 500 €) = 105 €
b)
(p % von 200 €) = 25 €
(p % von 920 kg) = 312,2 kg
c)
(p % von 102 m) = 25,24 m
(p % von 35,2 m²) = 12,15 m²
d)
(p % von 5 m) = 5 cm
(p % von 32 kg) = 3200 g
3. Mathematik-Nachhilfe-Aufgabe: Bestimme den Grundwert.
a)
88 kg = (5 % von G)
32 € = (8 % von G)
b)
45 kg = (12 % von G)
12 km = (20 % von G)
c)
20,40 € = (85 % von G)
15,4 l = (48 % von G)
4. Mathe-Nachhilfe-Aufgabe: Ermittle jeweils die gesuchte Größe.
a)
Grundwert: 360 m
Prozentsatz: 12 %
Prozentwert: ?
b)
Grundwert: ?
Prozentsatz: 25 %
Prozentwert: 115 g
c)
Grundwert: 354 m²
Prozentsatz: ?
Prozentwert: 195 m²
d)
Grundwert: ?
Prozentsatz: 80 %
Prozentwert: 55 €
e)
Grundwert: 812 €
Prozentsatz: ?
Prozentwert: 95 €
f)
Grundwert: ?
Prozentsatz: 8 %
Prozentwert: 2 €
Lösungen zum Mathe-Stoffgebiet Prozentrechnen
1. Mathematik-Nachhilfe-Aufgabe: Berechne den Prozentwert.
a) 15 % von 200 €
Die Formel zur Berechnung des Prozentwertes ist diese:
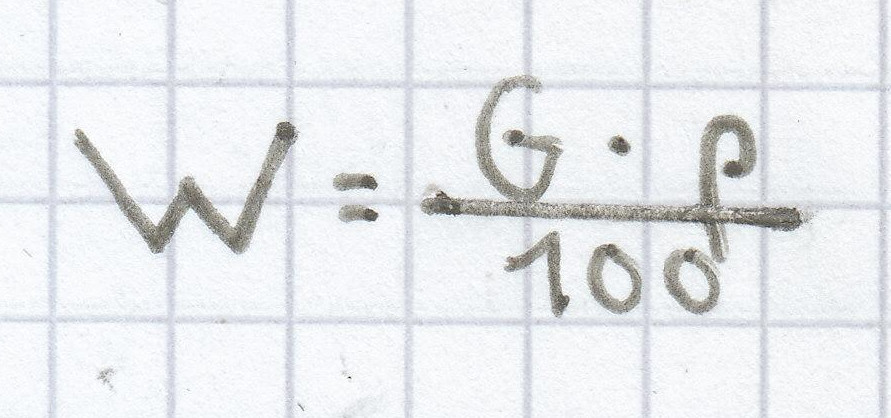
; daher ergibt sich folgende Rechnung:
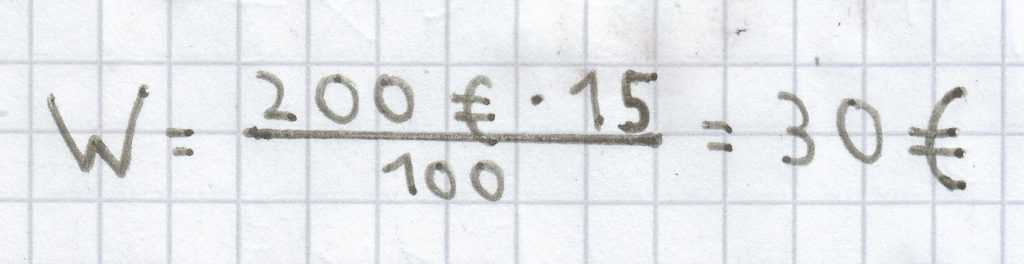
Der Prozentwert ist hier 30 €.
a) 80 % von 800 kg
Wieder muss folgende Formel zur Berechnung des Prozentwertes herangezogen werden:
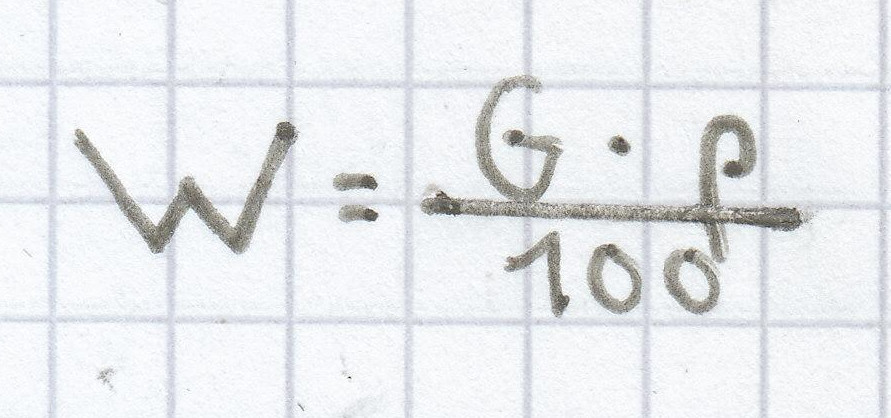
; deshalb ergibt sich:
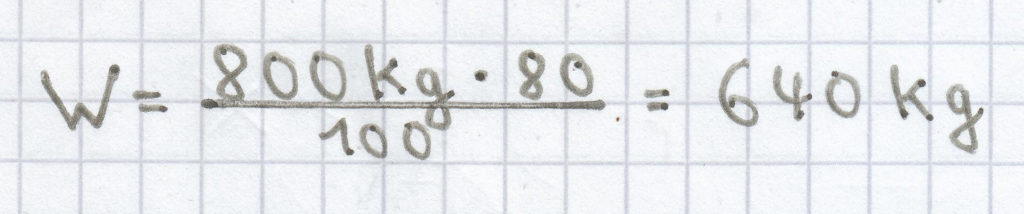
Der gesuchte Prozentwert ist hier 640 kg.
a) 5 % von 550 m²
Die Formel ist wieder folgende:
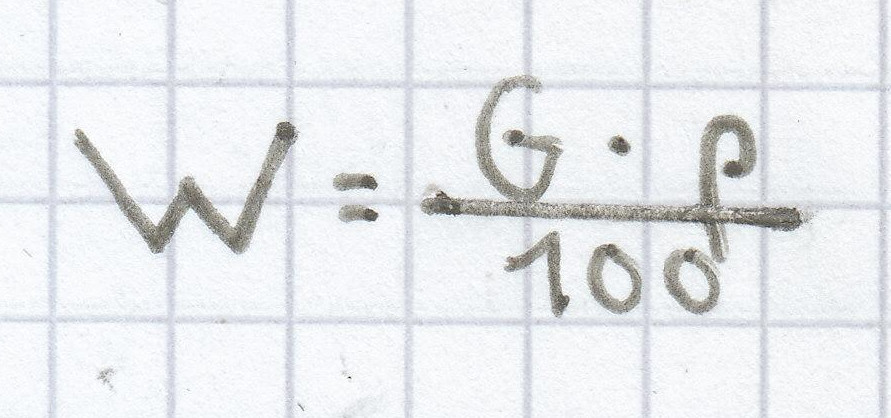
; deshalb kommt als Prozentwert dieses heraus:
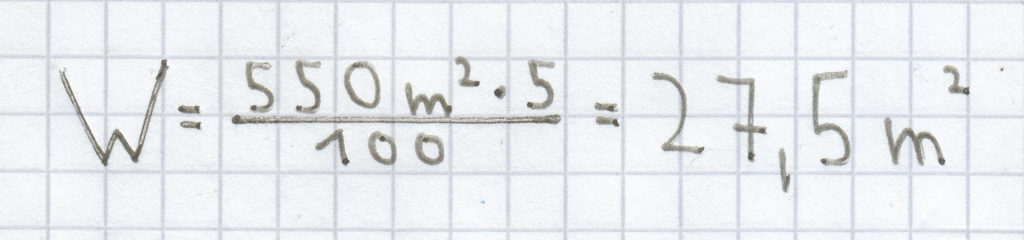
Der Prozentwert ist hier 27,5 m².
a) 20,5 % von 320 l
Die Formel zur Berechnung des Prozentwertes die diese:
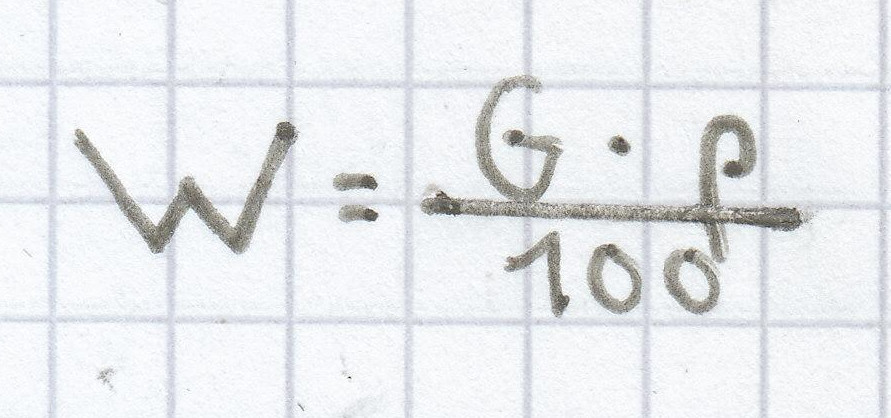
; daher ergibt sich folgende Rechnung:
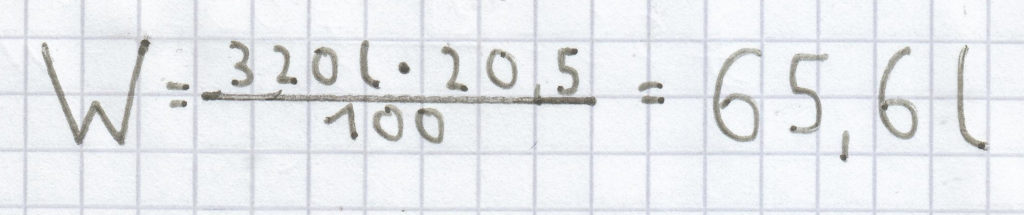
Als Prozentwert ergibt sich hier 65,6 l.
a) 100 % von 322 cm
Wieder muss hier diese Formel herangezogen werden:
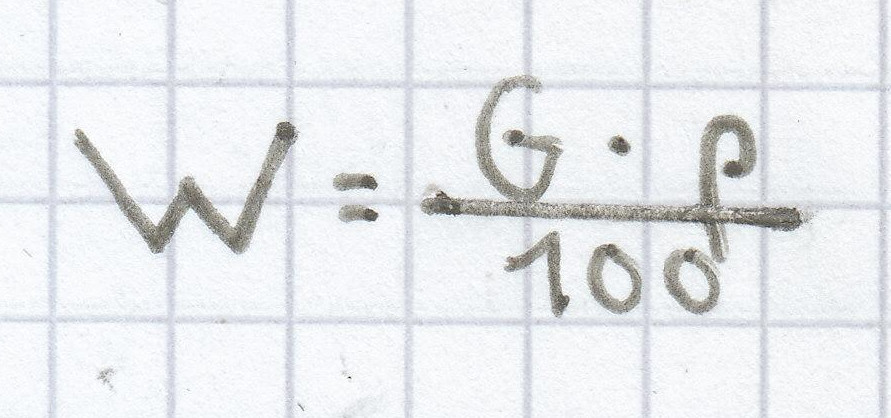
; folgende Rechnung ergibt sich:
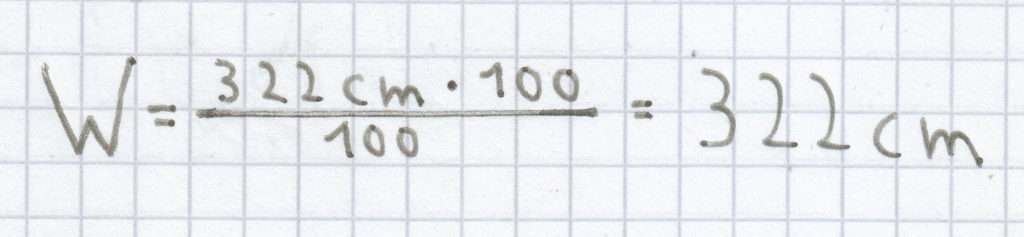
Der Prozentwert ist hier 322 cm.
b) 4 % von 520 t
Folgende Formel muss hier wieder verwendet werden:
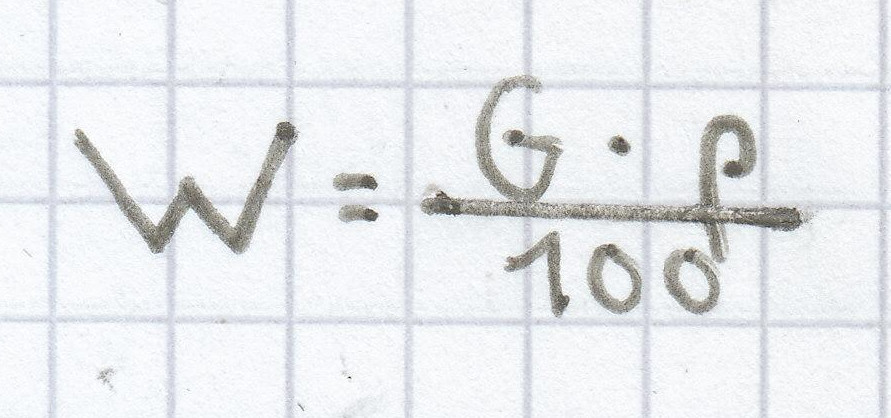
; dadurch ergibt sich diese Rechnung:
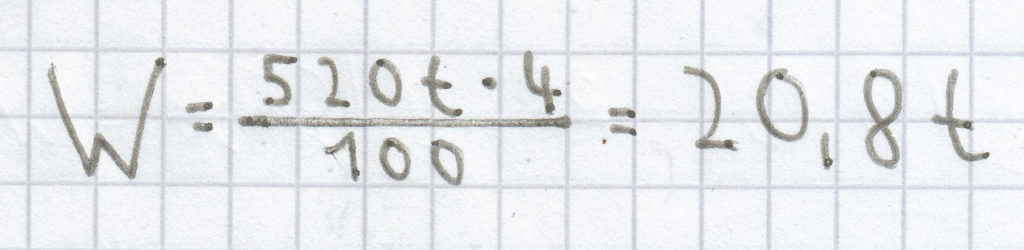
Der Prozentwert beträgt hier 20,8 t.
b) 82 % von 240 €
Zur Berechnung des Prozentwertes ist wiederum diese Formel vonnöten:
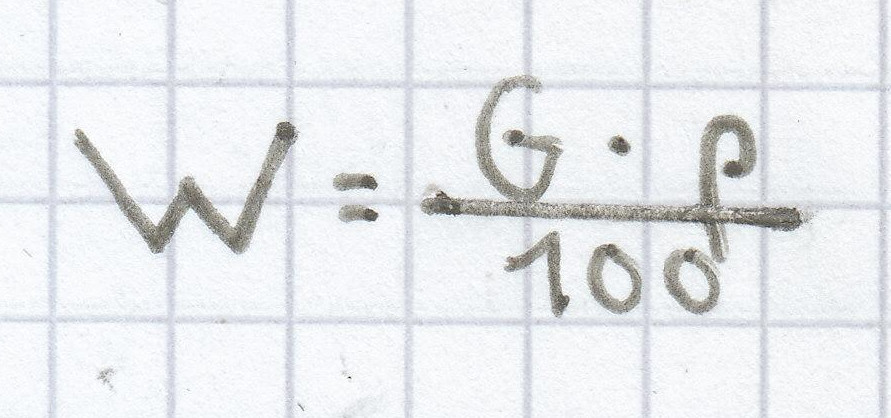
; folgende Berechnung ergibt sich hierdurch:
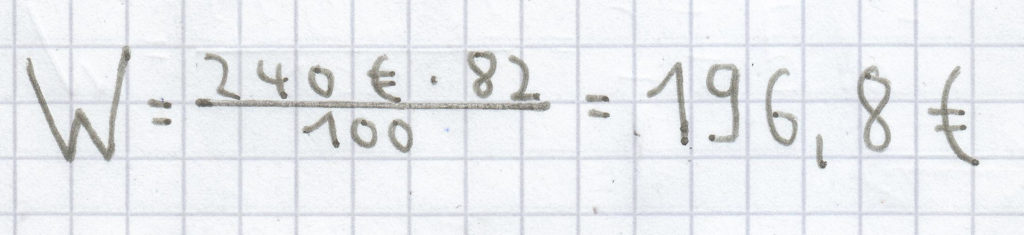
Der Prozentwert ist hier 196,8 €.
b) 15 % von 220 l
Diese Formel muss wiederum herangezogen werden:
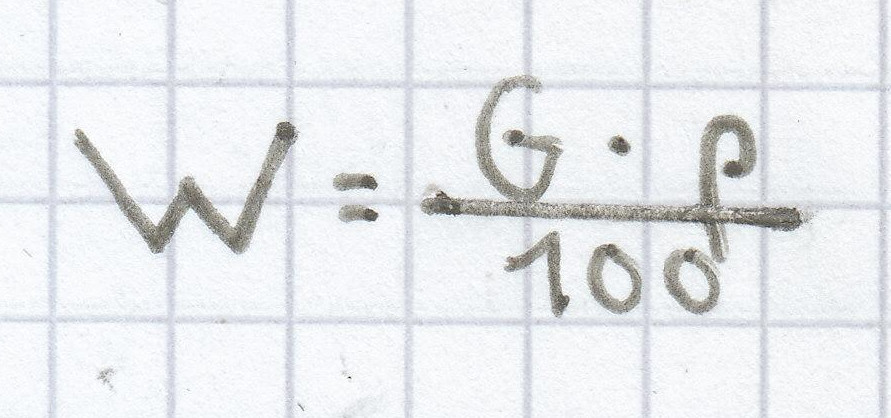
; diese Berechnung ergibt sich dann:
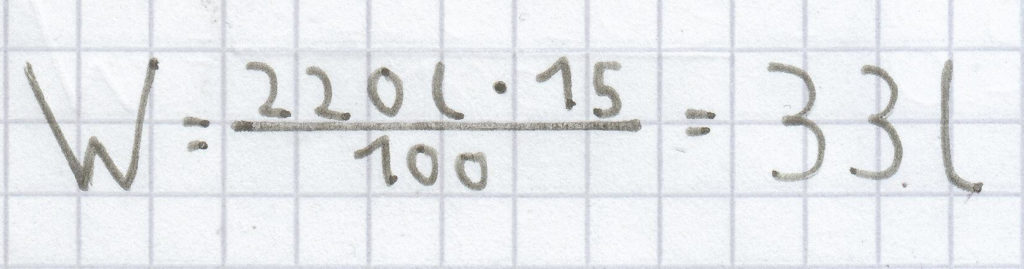
Als Prozentwert ergibt sich hier 33 l.
b) 51 % von 820 kg
Zur Berechnung der Prozentwertes benutzt man folgende Formel:
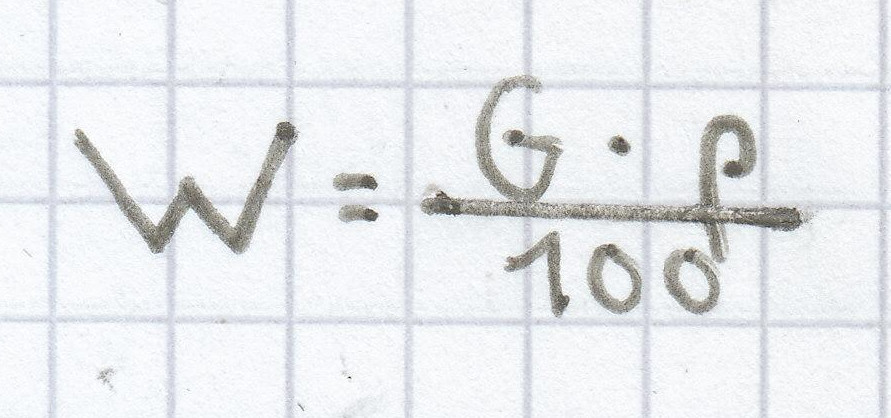
; diese Rechnung ergibt sich dann:
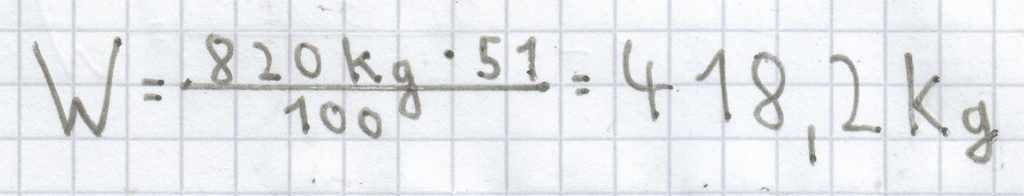
Der Prozentwert ist hier 418,2 kg.
b) 2 % von 350 m³
Den Prozentwert berechnet man wiederum mit dieser Formel:
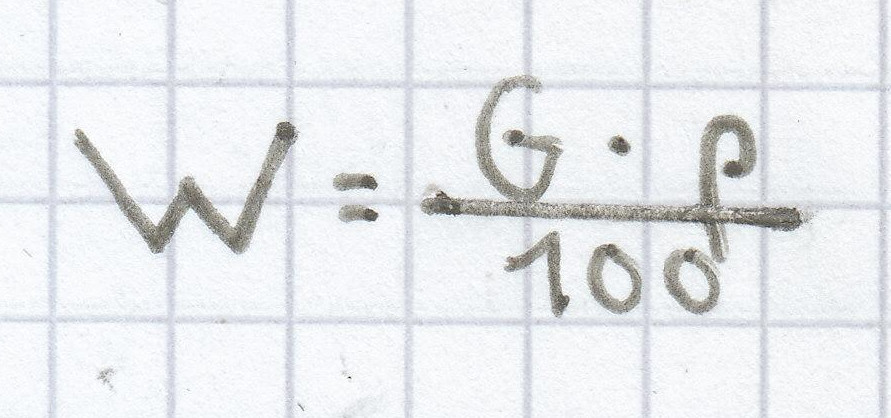
; folgende Rechnung ergibt sich dann:
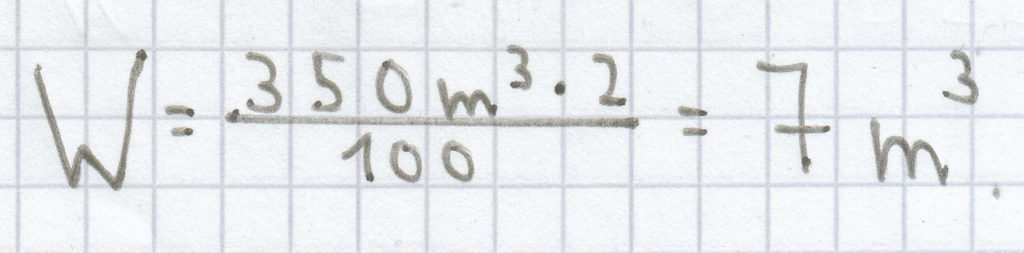
Als Prozentwert ergibt sich hier 7 m³.
c) 15,4 % von 250 l
Wiederum muss diese Formel herangezogen werden:
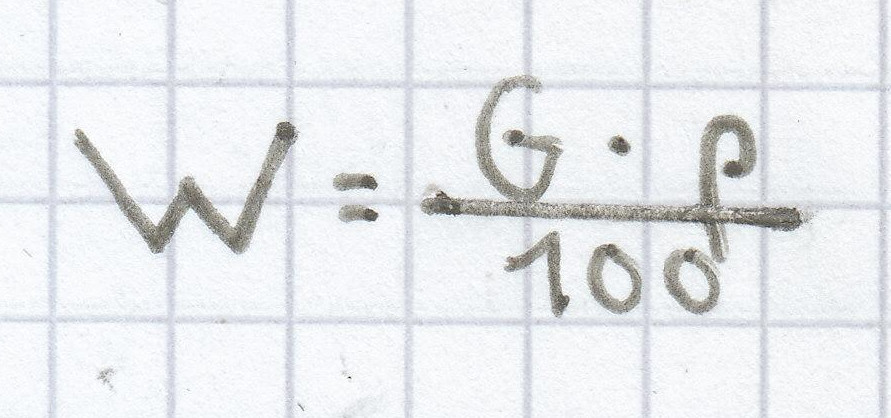
; als Rechnung ergibt sich sodann:
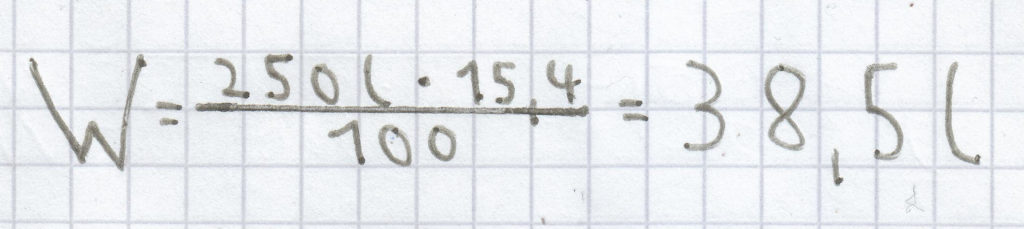
Die Höhe des Prozentwertes ist hier 38,5 l.
c) 20,2 % von 140 €
Die hier heranzuziehende Formel ist wiederum:
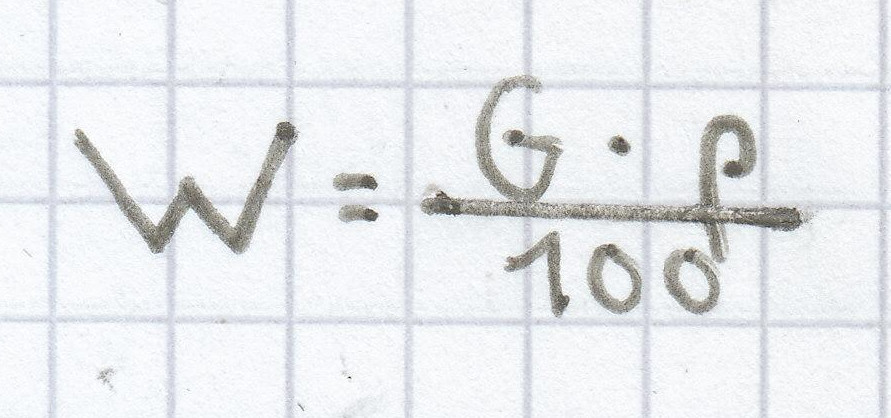
; folgende Rechnung kommt dadurch zustande:
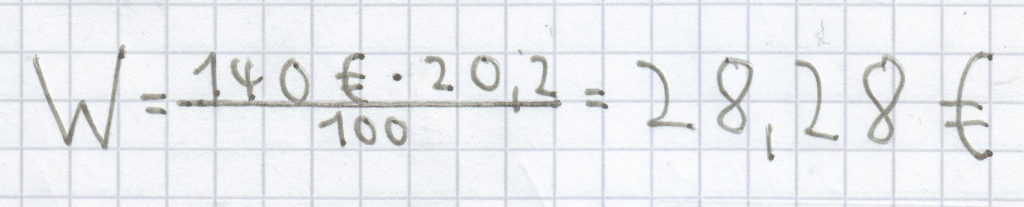
Als Prozentwert ergibt sich hier 28,28 €.
c) 82,5 % von 40 kg
Wiederum muss diese Formel herangezogen werden:
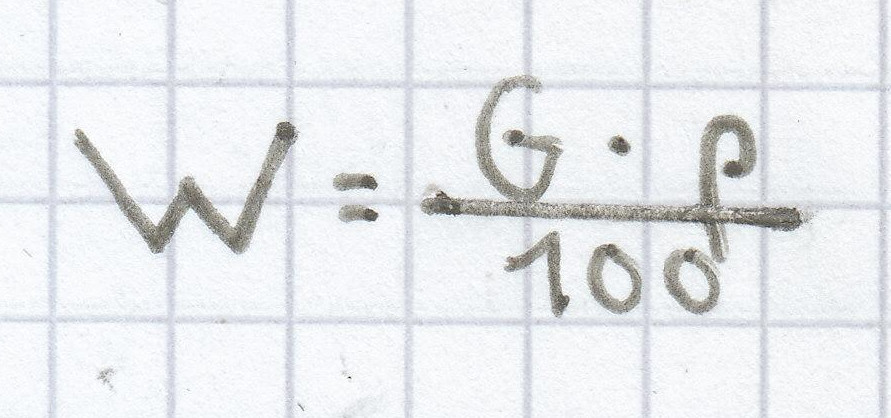
; dadurch ergibt sich erneut diese Rechnung:
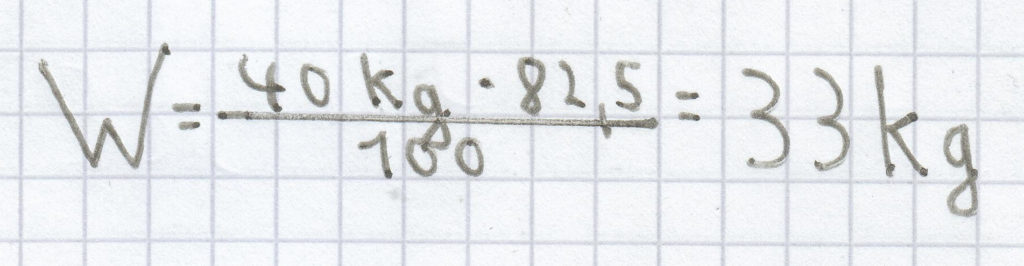
Der Prozentwert ist hier 33 kg.
c) 8,5 % von 34 €
Diese Formel muss zur Berechnung des Prozentwertes benutzt werden:
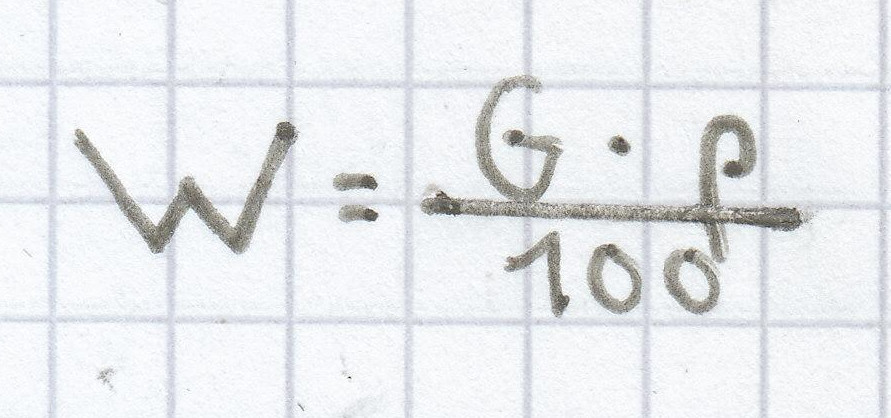
; als Rechnung ergibt sich dann:
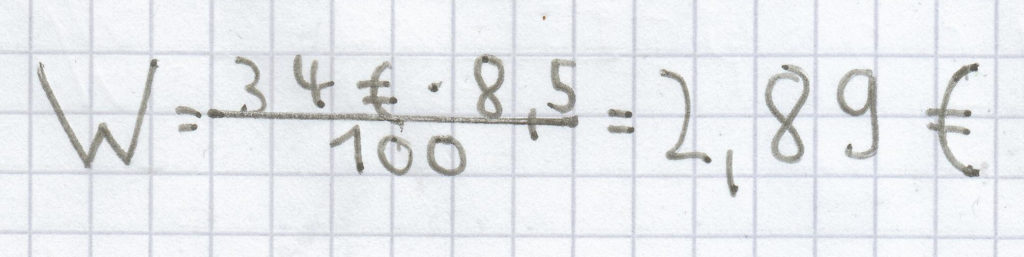
Die Höhe des Prozentwertes ist hier 2,89 €.
c) 33,3% von 1200 m
Wiederum muss man folgende Formel heranziehen:
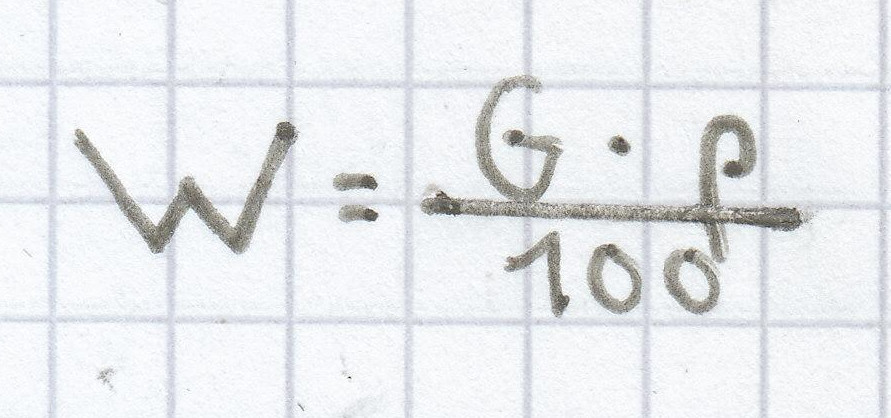
; diese Rechnung ergibt sich dadurch:
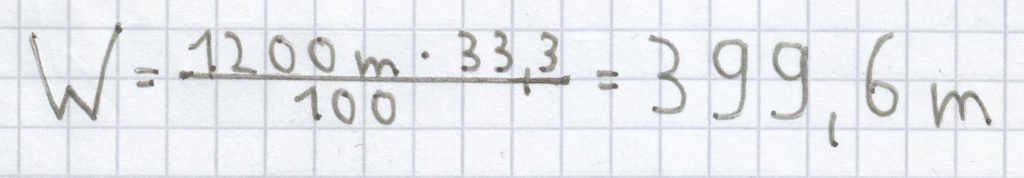
Der Prozentwert ist hier 399,6 m.

2. Mathematik-Nachhilfe-Aufgabe: Bestimme den Prozentsatz.
a) (p % von 120 €) = 63 €
Zur Berechnung des Prozentsatzes muss diese Formel herangezogen werden:
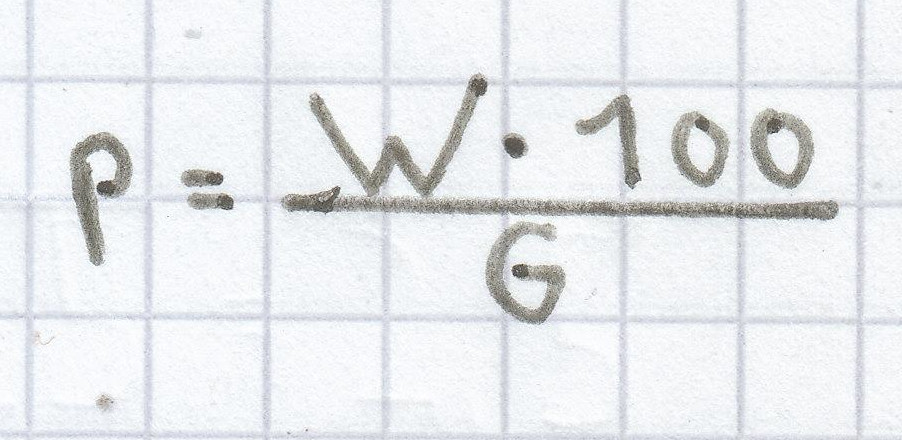
; hierdurch ergibt sich folgende Berechnung:
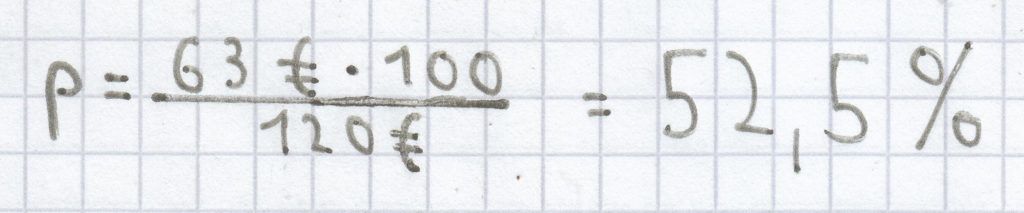
Der Prozentsatz ist hier 52,5 %.
a) (p % von 500 €) = 105 €
Wiederum muss folgende Formel benutzt werden:
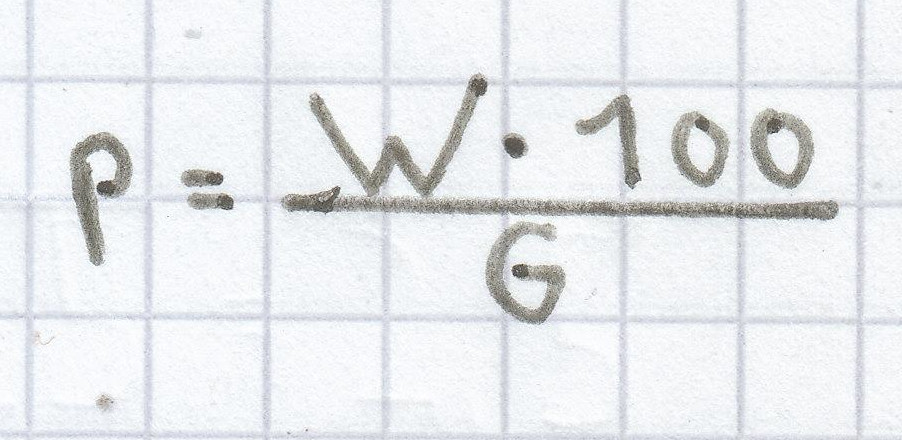
; somit ergibt sich diese Rechnung:
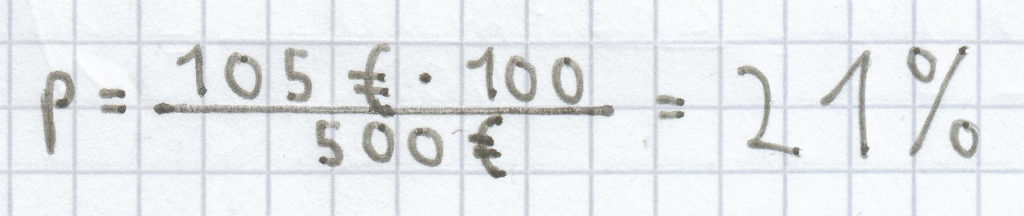
der Prozentsatz beträgt hier 21 %.
b) (p % von 200 €) = 25 €
Zur Berechnung des Prozentsatzes muss man wiederum diese Formel verwenden:
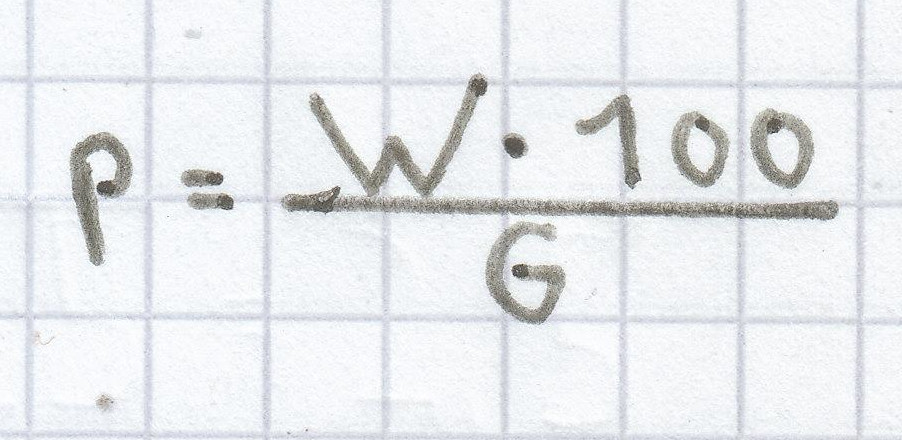
; dadurch ergibt sich:
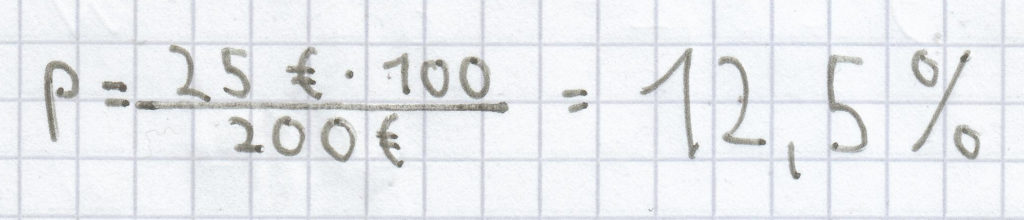
Der Prozentsatz ist hier 12,5 %.
b) (p % von 920 kg) = 312,2 kg
Wiederum ist folgende Formel hier heranzuziehen:
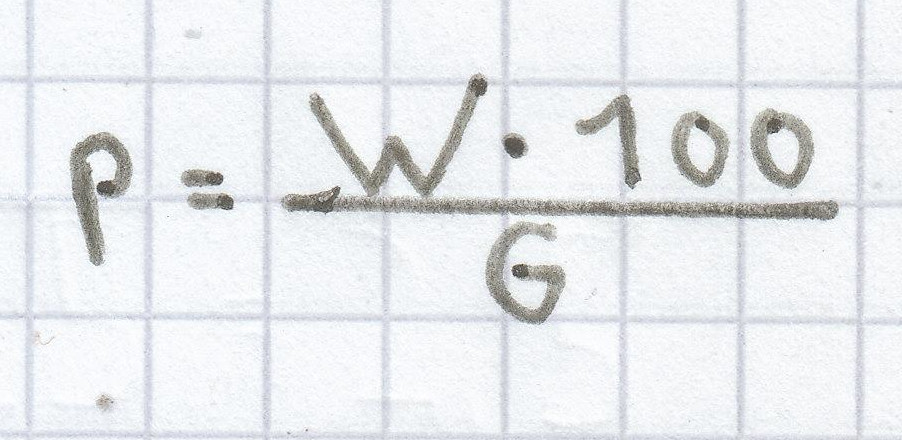
; der Prozentsatz ergibt sich dann, wie folgt:
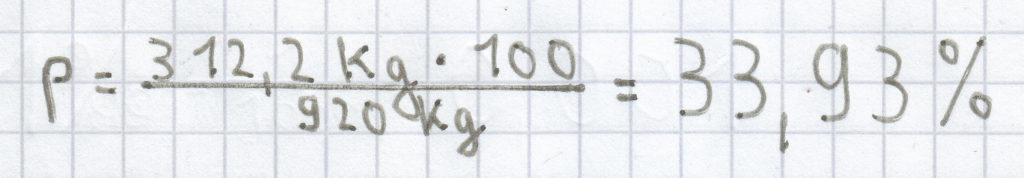
(gerundet auf zwei Nachkommastellen)
Der Prozentsatz beträgt hier 33,93 %.
c) (p % von 102 m) = 25,24 m
Zur Berechnung des Prozentsatzes benutzt man diese Formel:
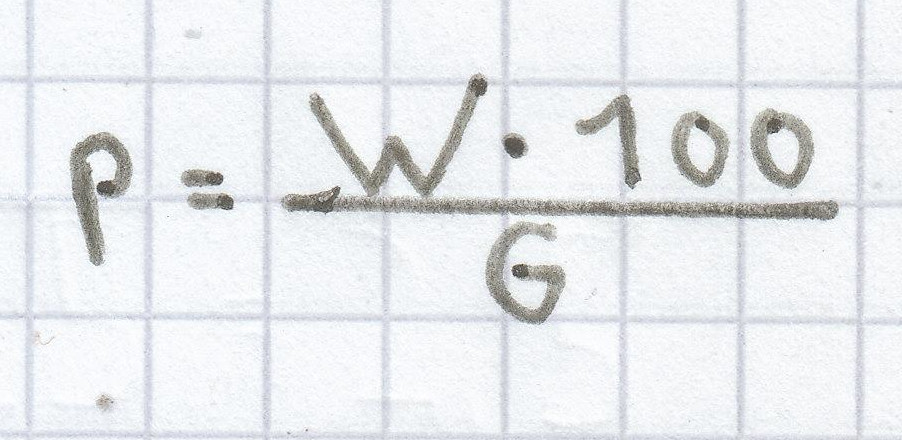
; folgende Rechnung ergibt sich somit:
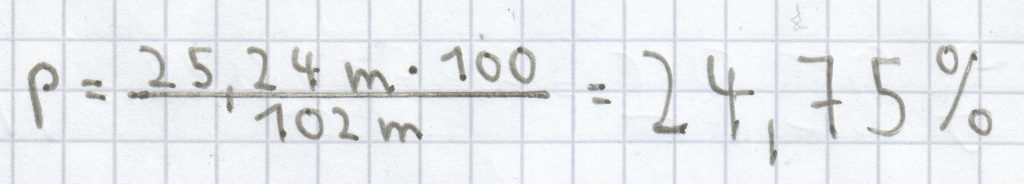
(gerundet auf zwei Nachkommastellen)
Die Höhe des Prozentsatzes ist hier 24,75 %.
c) (p % von 35,2 m²) = 12,15 m²
Wiederum ist hier folgende Formel vonnöten:
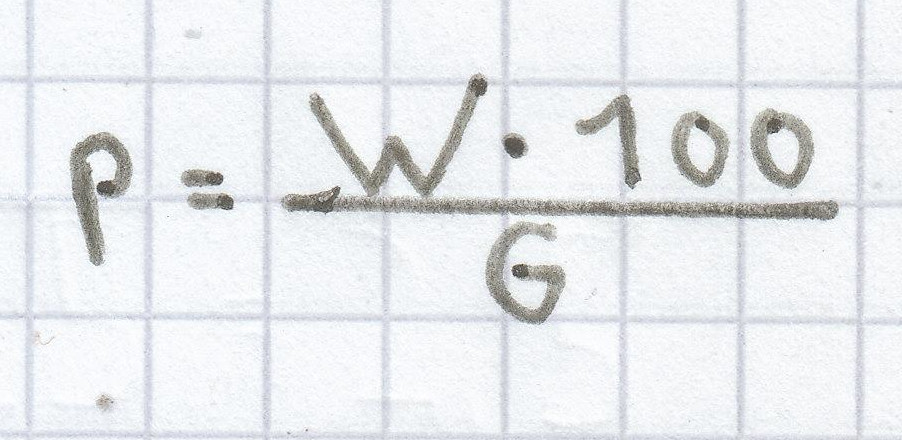
; dadurch ergibt sich diese Berechnung des Prozentsatzes:
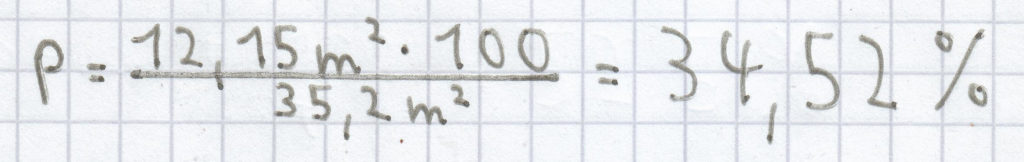
(gerundet auf zwei Nachkommastellen)
Der Prozentsatz beträgt hier 34,52 %.
d) (p % von 5 m) = 5 cm
Hier ist zu beachten, dass man vorab die Größen-Einheiten einander anpasst. Entweder rechnet man die Längen-Einheit m in cm um oder die Längen-Einheit cm in m. 5 m = (mal 10, mal 10) = 500 cm bzw. 5 cm = (geteilt durch 10, geteilt durch 10) = 0,05 m.
Wiederum muss diese Formel hier benutzt werden:
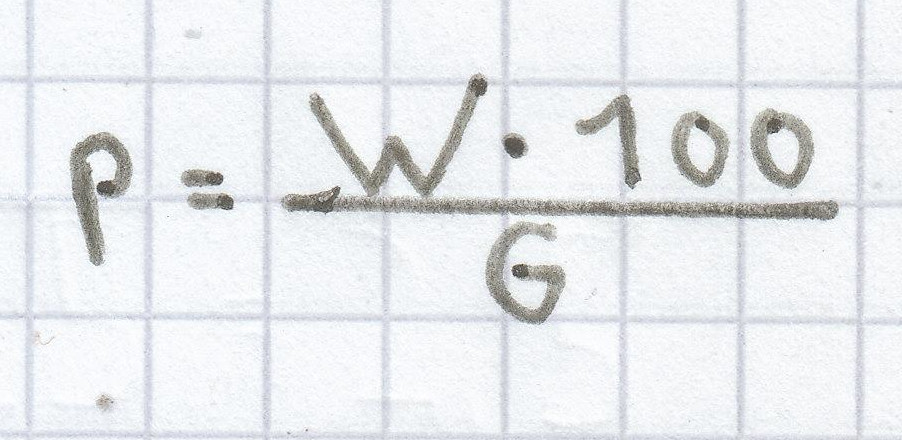
; folgende Rechnung ergibt sich somit:
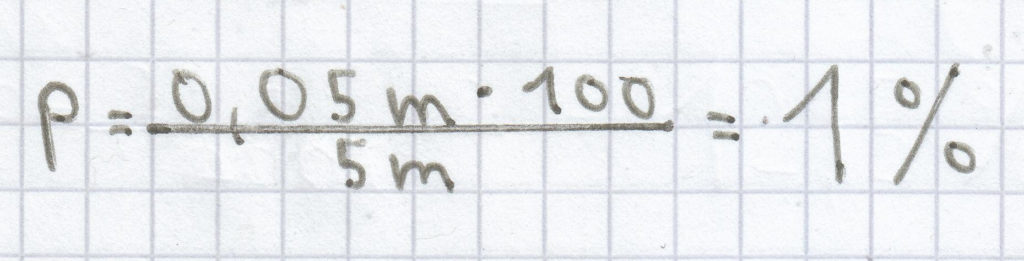
Der Prozentsatz ist hier 1 %.
d) (p % von 32 kg) = 3200 g
Hier muss man auch zuerst die beiden Größeneinheiten aufeinander anpassen. 32 kg = (mal 1000) = 32000 g; 3200 g (geteilt durch 1000) = 3,2 kg.
Wiederum muss man hier diese Formel heranziehen:
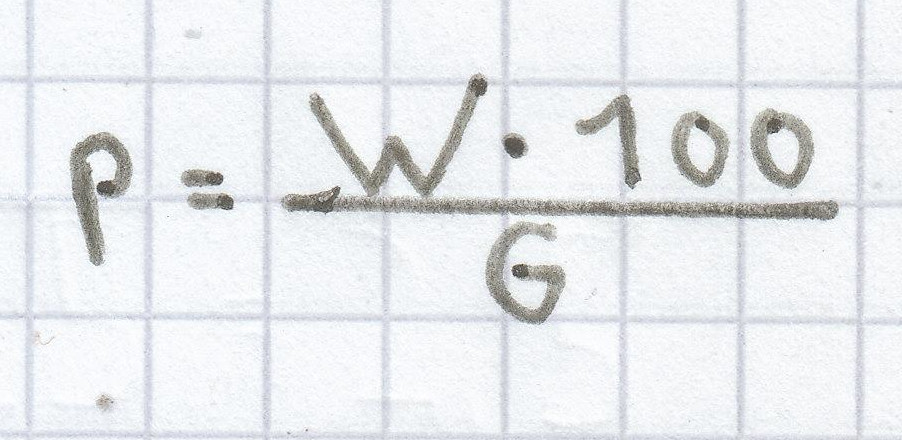
; darauf kann man den Prozentsatz berechnen:
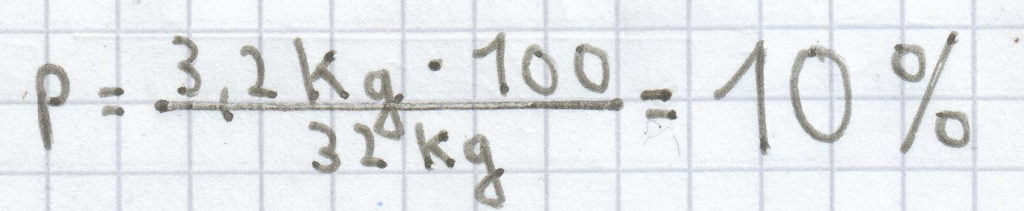
Die Höhe des Prozentsatzes ist hier 10 %.
3. Mathe-Nachhilfe-Aufgabe: Ermittle den Grundwert.
a) 88 kg = (5 % von G)
Die Formel zur Berechnung des Grundwerts ist folgende:
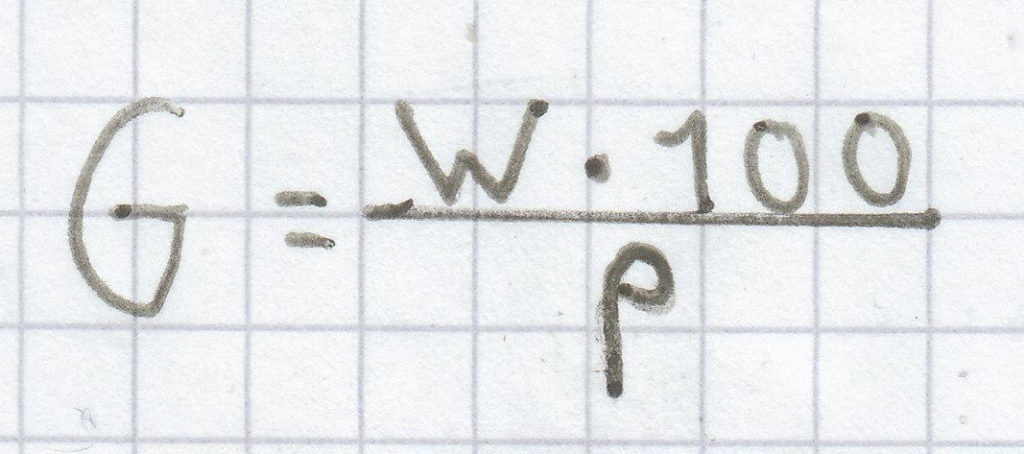
; hieraus ergibt sich diese Berechnung:
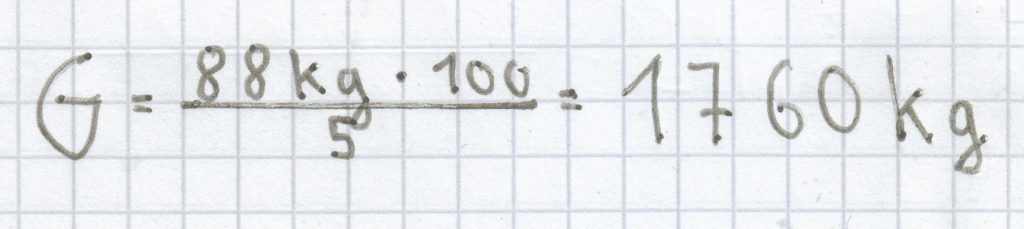
Der Grundwert ist hier 1760 kg.
a) 32 € = (8 % von G)
Wiederum muss man hier diese Formel verwenden:
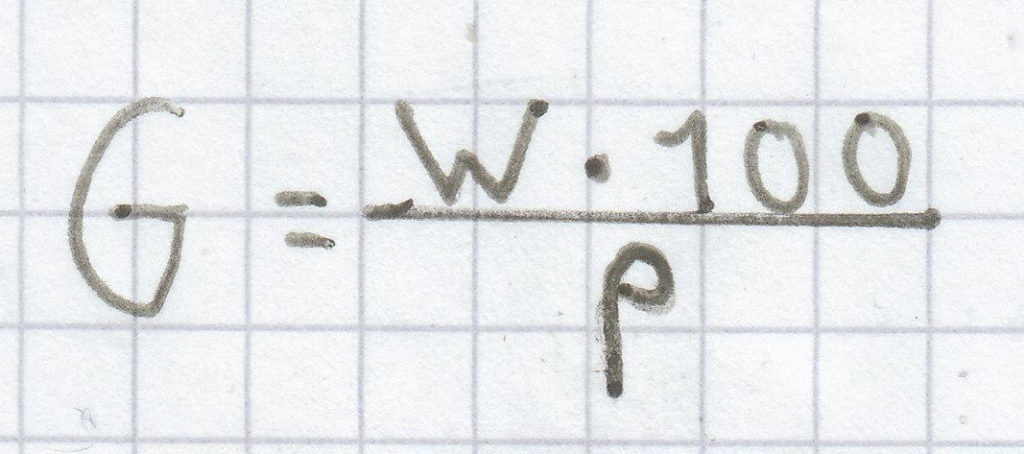
; der Grundwert ergibt sich nun wie folgt:
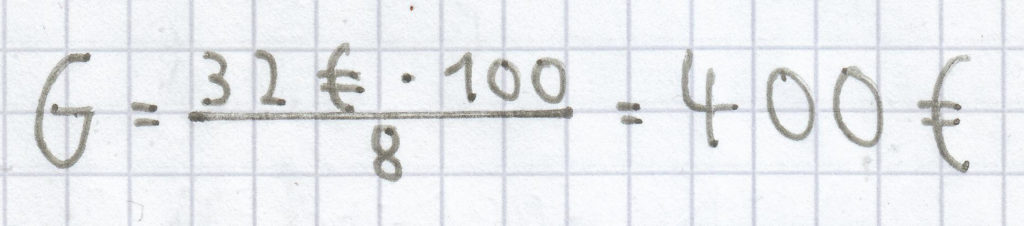
Der Grundwert beträgt hier 400 €.
b) 45 kg = (12 % von G)
Zur Berechnung des Grundwerts muss wiederum diese Formel herangezogen werden:
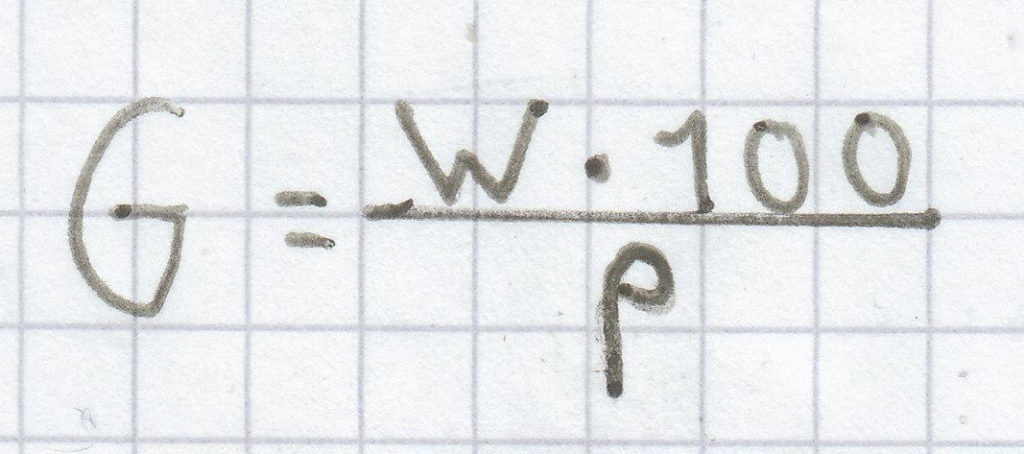
; hierdurch ergibt sich diese Rechnung:
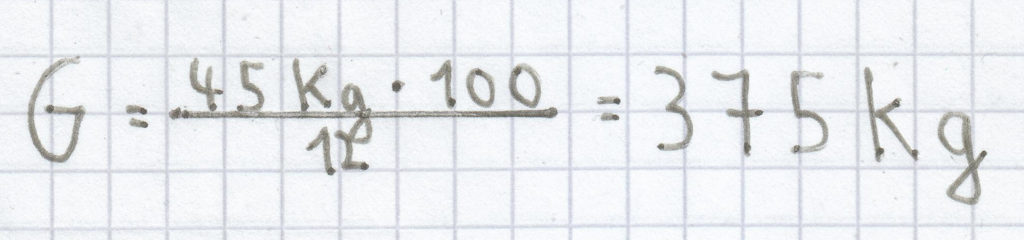
Die Höhe des Grundwerts ist hier 375 kg.
b) 12 km = (20 % von G)
Der Grundwert berechnet man mittels dieser Formel:
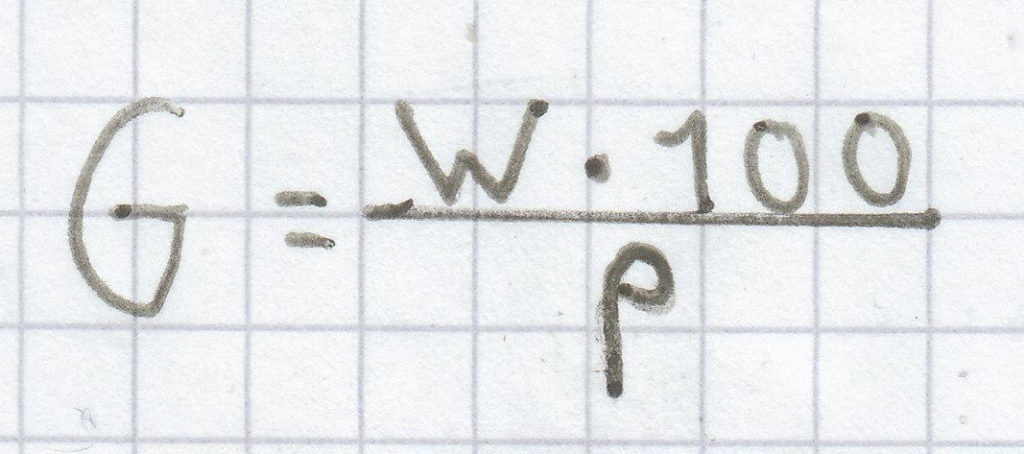
; dadurch kommt es zu dieser Rechnung:
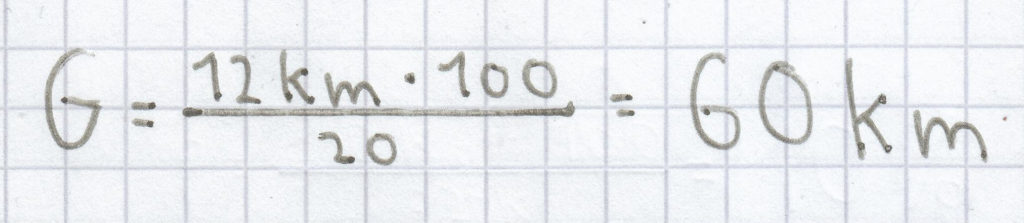
Der Grundwert beträgt hier 60 km.
c) 20,40 € = (85 % von G)
Wiederum muss hier folgende Formel zur Berechnung des Grundwerts herangezogen werden: Dadurch ergibt sich folgende Berechnung:
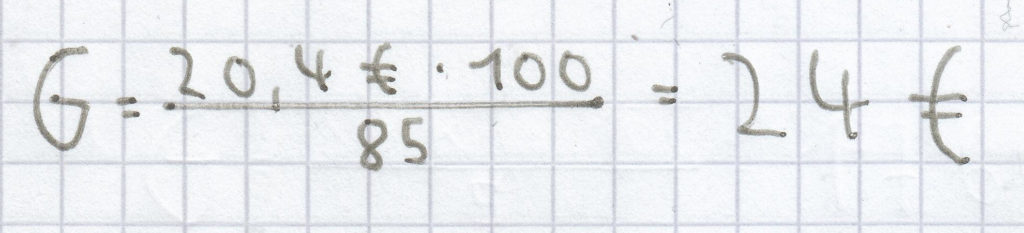
Der Grundwert ist hier 24 €.
c) 15,4 l = (48 % von G)
Wiederum muss hier diese Formel verwendet werden:
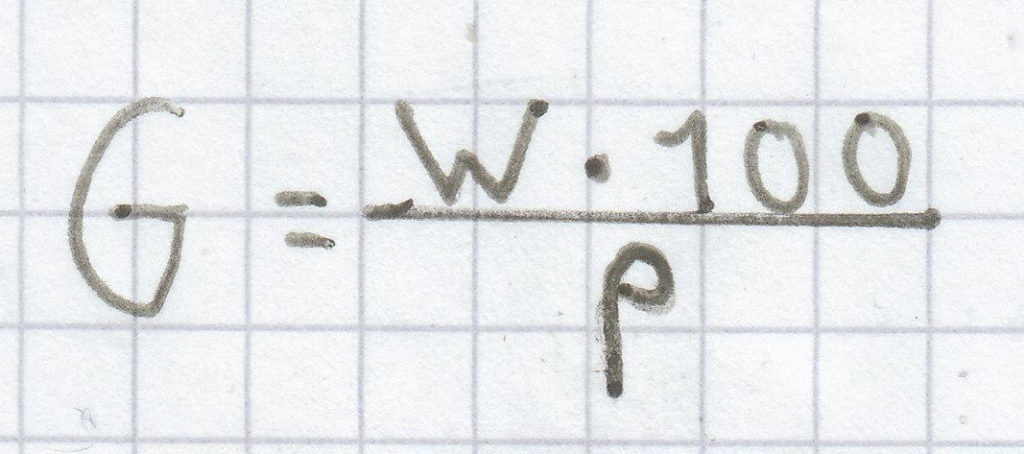
; dadurch ergibt sich folgende Berechnung:
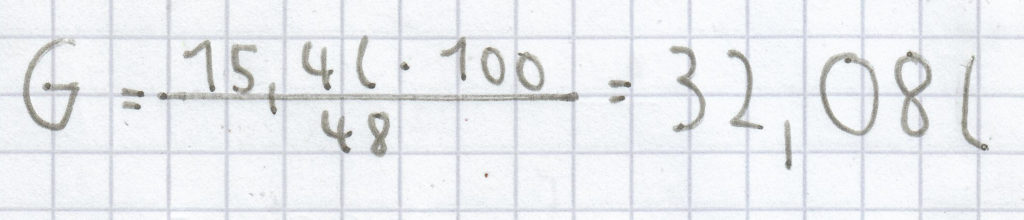
(gerundet auf zwei Nachkommastellen)
Der Grundwert beträgt hier 32,08 l.
4 Mathe-Nachhilfe-Aufgabe: Berechne die fehlende Größe.
a) Grundwert: 360 m, Prozentsatz: 12%. Hier ist der Prozentwert gesucht. Daher ist hier diese Formel vonnöten:
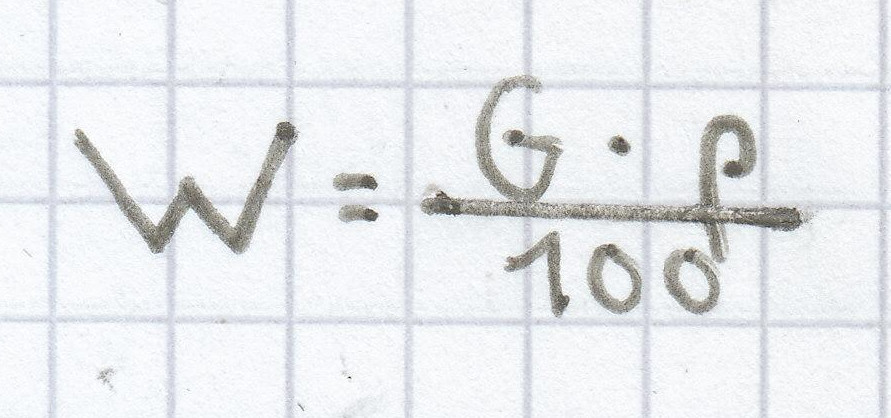
; eingesetzt ergibt sich:
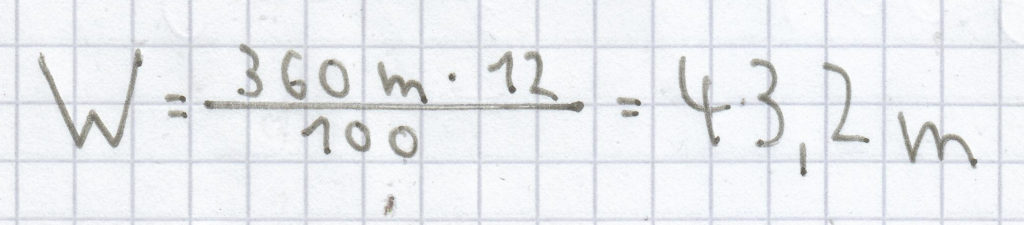
Der Prozentwert ist hier 43,2 m.
b) Prozentsatz: 25 %, Prozentwert: 115 g. Hier ist der Grundwert gesucht. Daher muss man hier folgende Formel heranziehen:
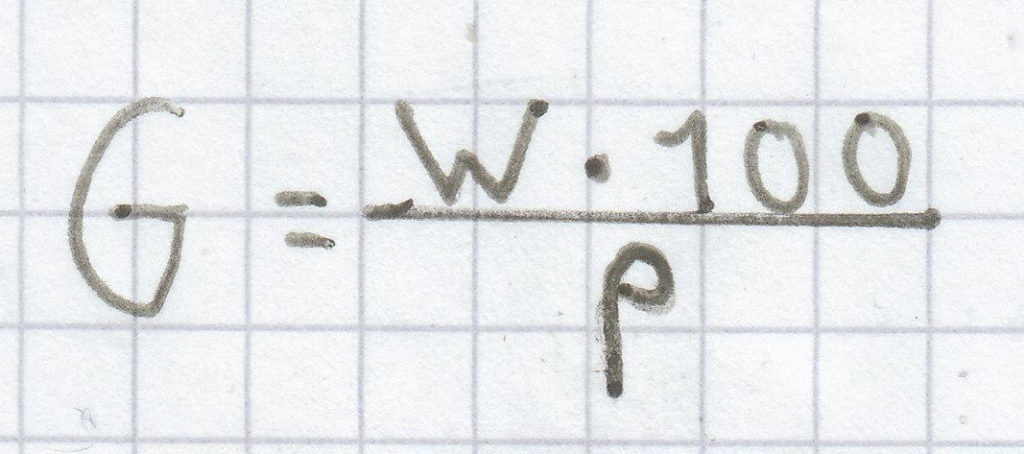
; daraus ergibt sich diese Rechnung:
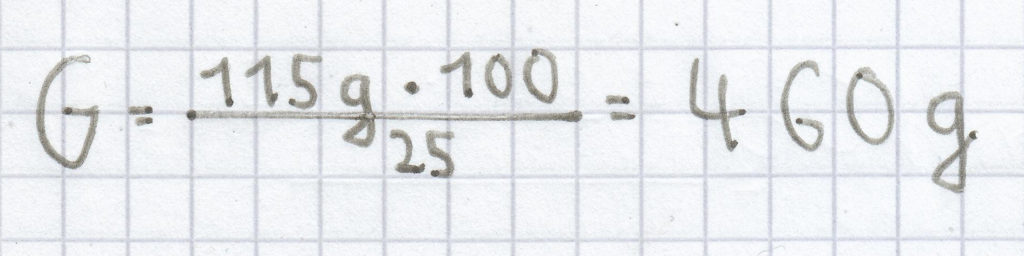
Der Grundwert beträgt hier 460 g.
c) Grundwert: 354 m² , Prozentwert: 195 m². Hier der der Prozentsatz gesucht. Daher ist hier diese Formel vonnnöten:
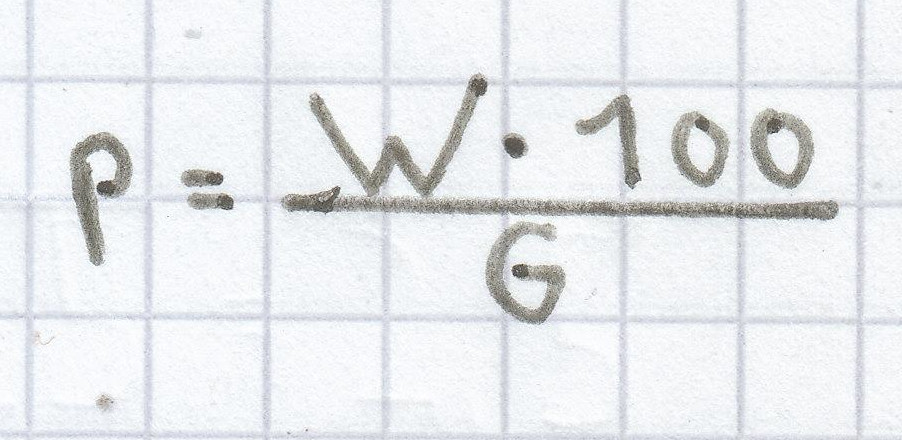
. Eingesetzt ergibt sich:
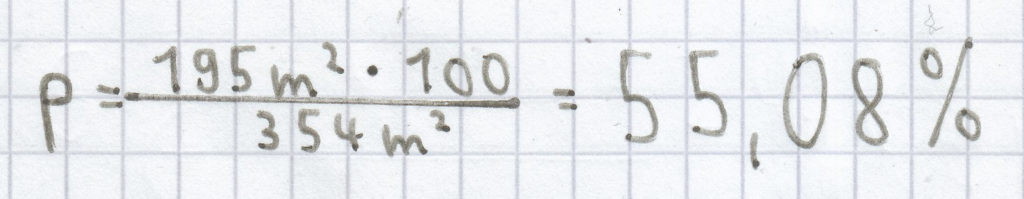
(gerundet auf zwei Nachkommastellen)
Der Prozentsatz ist hier 55,08 %.
d) Prozentsatz: 80 %, Prozentwert: 55 €. Hier ist der Grundwert gesucht. Daher muss man hier diese Formel heranziehen:
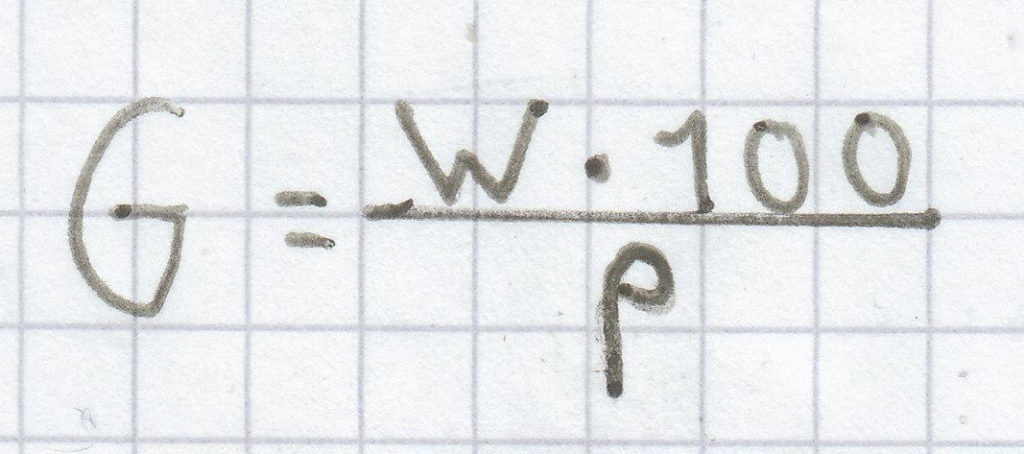
; eingesetzt ergibt sich:
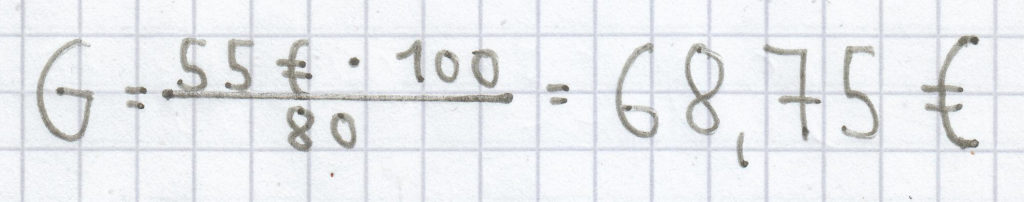
Der Grundwert beträgt hier 68,75 €.
e) Grundwert: 812 €, Prozentwert: 95 €. Der Prozentsatz ist hier gesucht. Daher muss man hier diese Formel heranziehen:
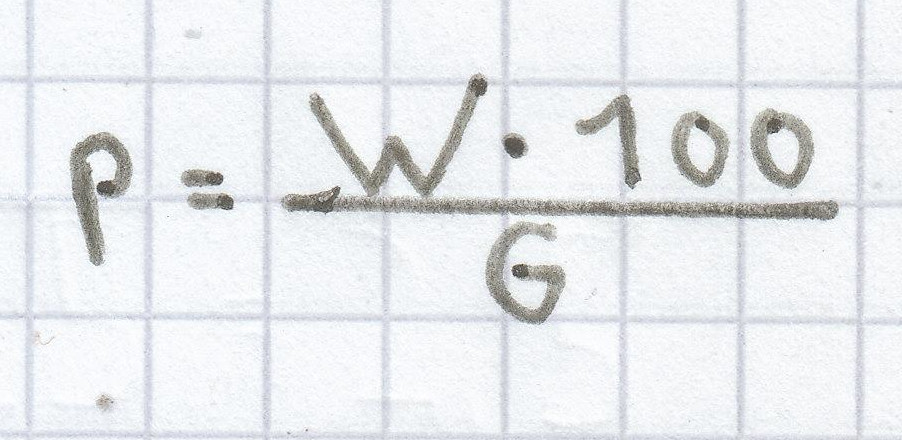
. Dadurch ergibt sich folgende Rechnung:
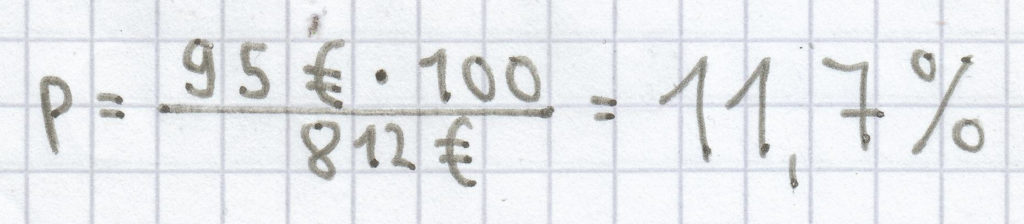
(gerundet auf zwei Nachkommastellen)
Der Prozentsatz ist hier 11,7 %.
f) Prozentsatz: 8 %, Prozentwert: 2 €. Hier ist der Grundwert gesucht. Daher muss hier diese Formel herangezogen werden:
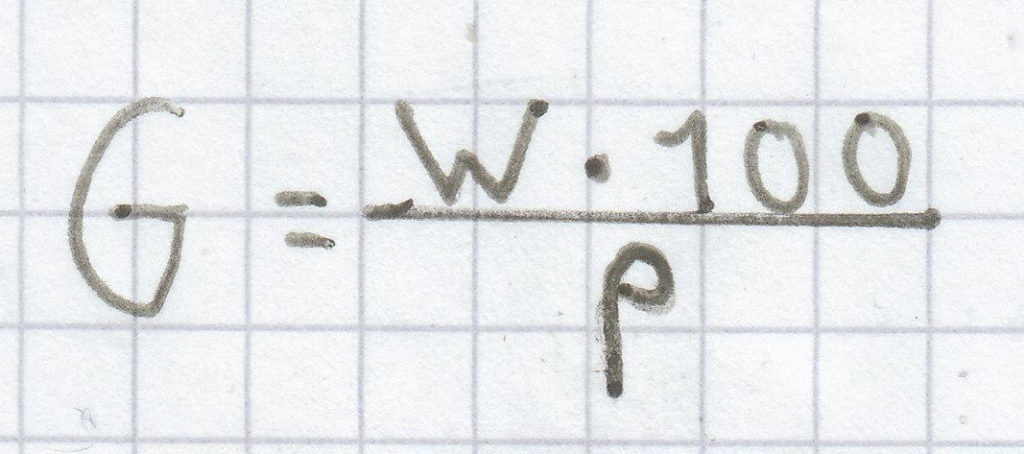
; dadurch ergibt sich folgende Rechnung:
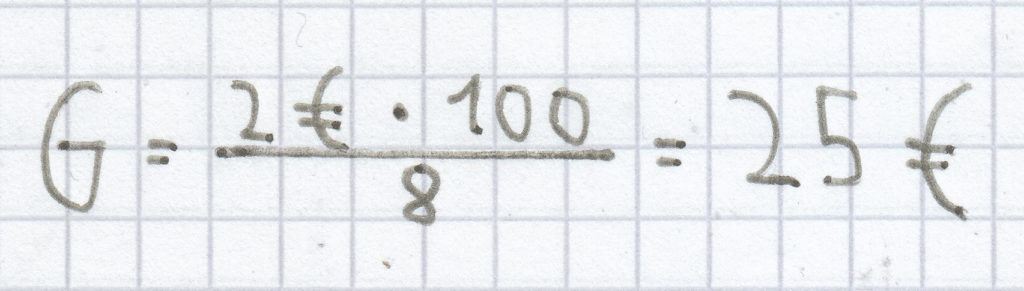
Der Grundwert beträgt hier 25 €.