Bei quadratischen Gleichungen kann man mittels der p-q-Formel, der Mitternachtsformel oder eines quadratischen Ergänzens deren Lösungen ermitteln. Das sind ja alles bekanntermaßen Lösungsverfahren für quadratische Gleichungen. „Was aber, wenn die Lösung bereits vorliegt?“, sagt der Mathematik-Lehrer. „Schön“, sagt hier ein nicht so interessierter Mathe-Schüler. „Dann muss ich erst gar nicht rechnen.“ „Moment, das kann aber nicht sein,“ sagt hingegen eine an Mathematik eine Freude habende Schülerin. „Stimmt“, sagt schließlich der Lehrer. „Liegt eine Lösung einer quadratischen Gleichungen bereits vor, so soll man mittels eines Lösungsverfahren deren Normalform ermitteln!“, fährt dieser weiter. „Das macht man dann über den sogenannte Satz von Vieta, und zwar …“ „Mathe ist doch nie schön“, denkt sich schlussendlich der an dem Fach nicht interessierte Schüler.
Aufgaben zum Mathe-Stoffgebiet Quadratische Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der quadratischen Gleichung.
a) –(a – 7) (3a + 1) + (a – 5) (2a – 17) = 84
b) (r² + 2r – 15) (r² – 7r – 30) = 0
c) (4x + 3) (4x – 3) = 9 (x – 1)
d) 6a – 2 = (3 + a) (a – 3)
2. Mathe-Nachhilfe-Aufgabe: Es ist eine Lösungsmenge einer quadratischen Gleichung gegeben. Stelle hierfür mittels des Satz von Vieta eine quadratische Gleichung in der Normalform auf.
a) {4; 7}
b) {–3; 5}
c) { –0,6; –0,4}
d)
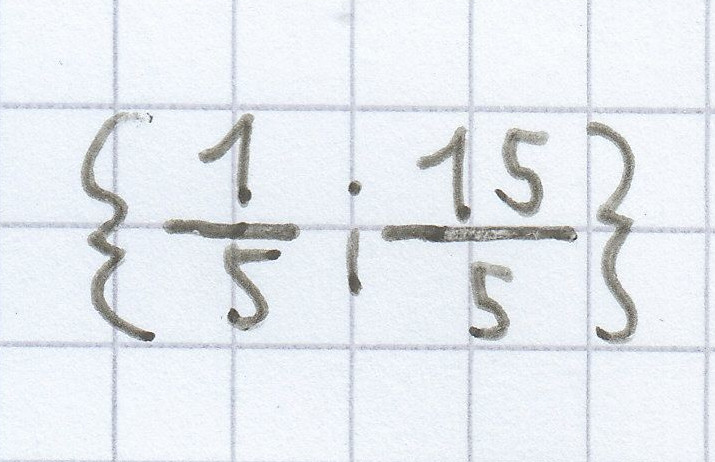
3. Mathematik-Nachhilfe-Aufgabe: Sind die angegebenen Lösungen wirklich die Lösungen der angegebenen quadratischen Gleichung? Falls nicht, verändere die Gleichung dahingehend, dass es sich um korrekte Lösungen handelt.
a) x² + 2x – 24 = 0 L = {4; –6}
b) y² + 3y + 2,25 = 0 L = {–1,5}
c) a² + 6a – 16 = 0 L = {–2; 8}
d) 4y² + 30y + 56 = 0 L = {–4; –3,5}
4. Mathe-Nachhilfe-Aufgabe: Ermittle die Länge und die Breite eines Rechtecks.
Bei einem Rechteck ist der Flächeninhalt 30 cm² und der Umfang 23 cm. Wie groß sind dessen Längen?
Lösungen zum Mathematik-Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der quadratischen Gleichung.
a) –(a – 7) (3a + 1) + (a – 5) (2a – 17) = 84
–(3a² – 21a + a – 7) + (2a² – 10a – 17a + 85) = 84
–3a² + 21a – a + 7 + 2a² – 10a – 17a + 85 = 84
–a² – 7a + 92 = 84 | – 84
–a² – 7a + 8 = 0 | · (–1)
a² + 7a – 8 = 0
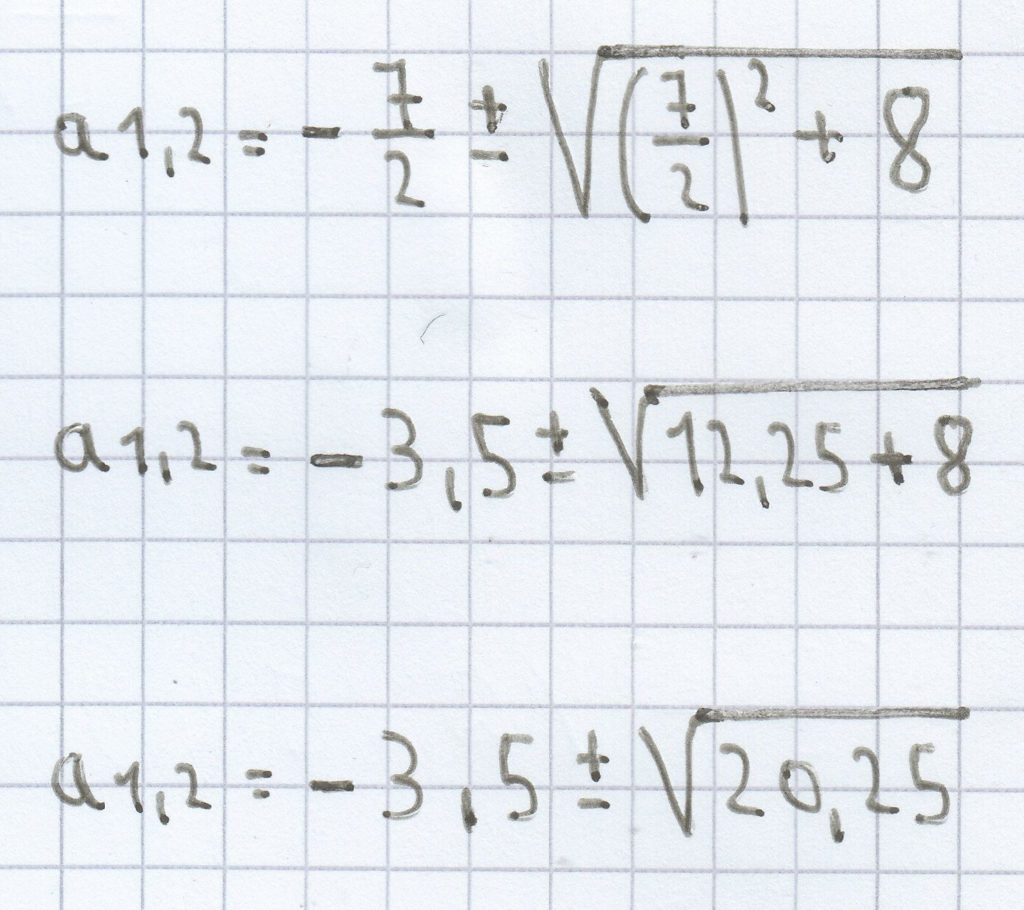
a1,2 = –3,5 ± 4,5
a1 = –3,5 + 4,5
a1 = 1
a2 = –3,5 – 4,5
a2 = –8
L = {–8; 1}
b) (r² + 2r – 15) (r² – 7r – 30) = 0
Hier gilt: Ist ein Faktor des Produkts gleich null, so ist das Produkt gleich null. Daher gibt es hier jeweils die zwei quadratische Gleichungen in den Klammern, die man lösen muss.
r² + 2r – 15 = 0
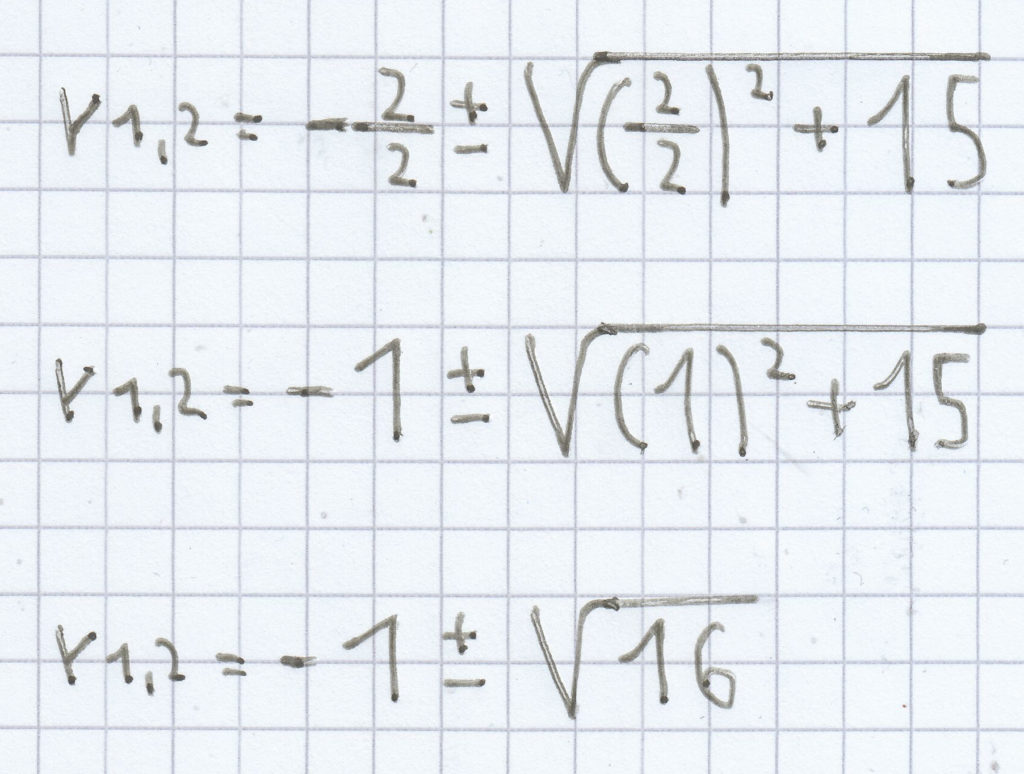
r1,2 = –1 ± 4
r1 = –1 + 4
r1 = 3
r2 = –1 – 4
r2 = –5
r² – 7r – 30 = 0
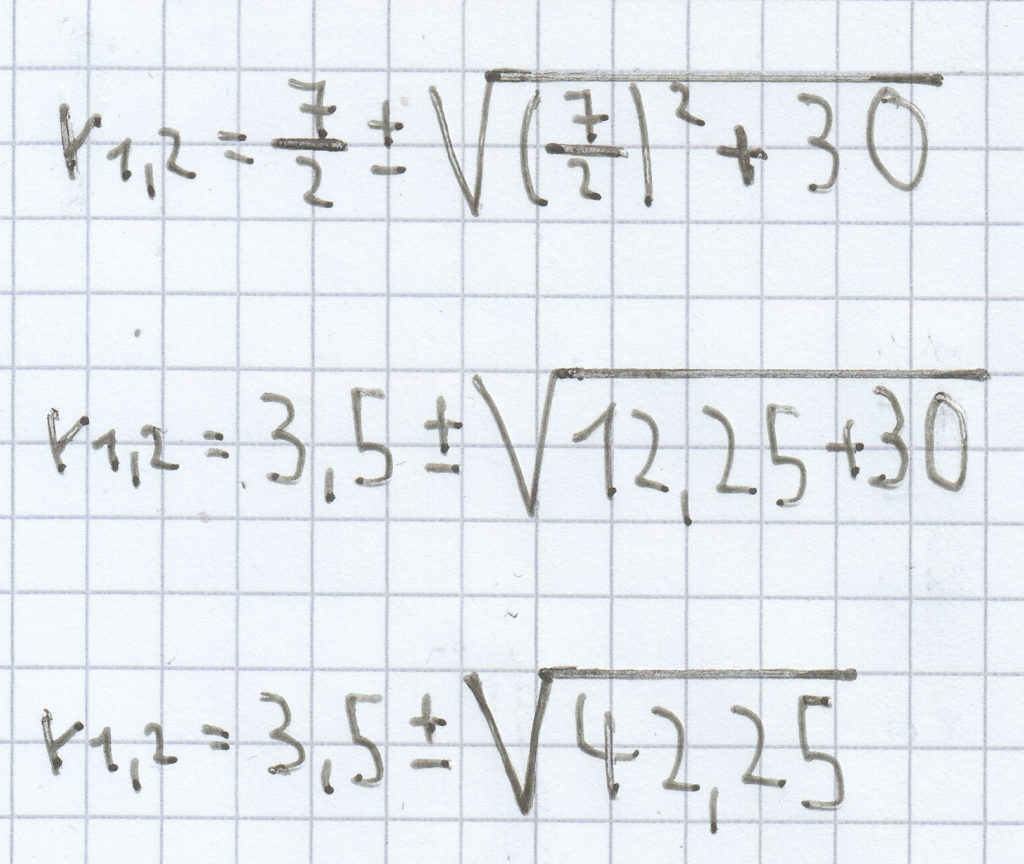
r1,2 = 3,5 ± 6,5
r1 = 3,5 + 6,5
r1 = 10
r2 = 3,5 – 6,5
r2 = –3
L = {–5; –3; 3; 10}
c) (4x + 3) (4x – 3) = 9 (x – 1)
16x² – 9 = 9x – 9 | + 9
16x² = 9x | – 9x
16x² – 9x = 0
x · (16x – 9) = 0
x1 = 0
16x – 9 = 0 | + 9
16x = 9 | : 16

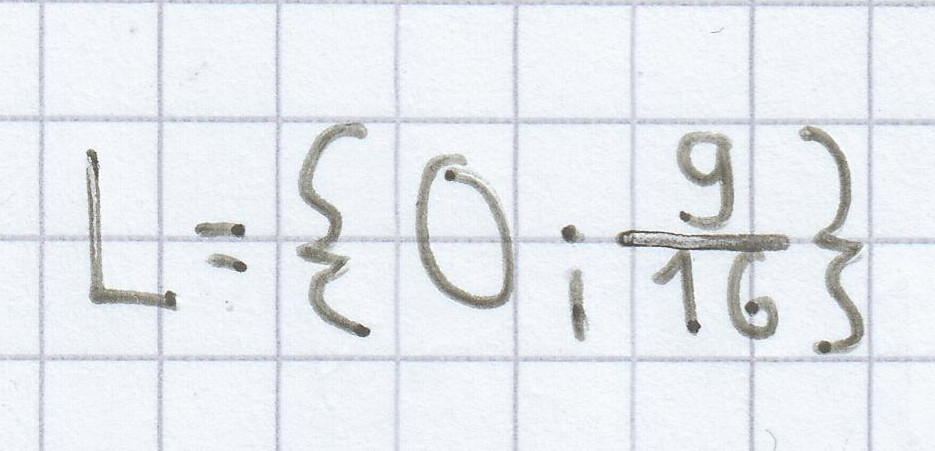
d) 6a – 2 = (3 + a) (a – 3)
6a – 2 = 3a + a² – 9 – 3a
6a – 2 = a² – 9 | + 2
6a = a² – 7 | – 6a
0 = a² – 6a – 7
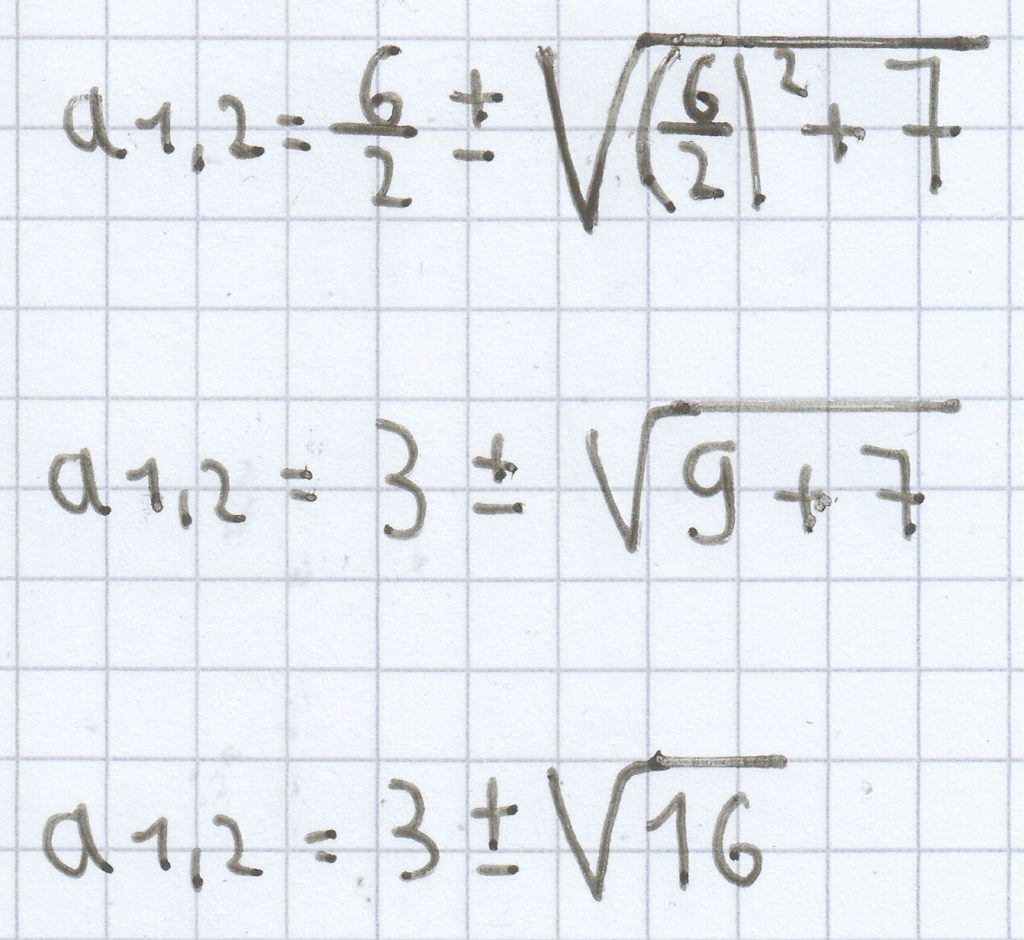
a1,2 = 3 ± 4
a1 = 3 + 4
a1 = 7
a2 = 3 – 4
a2 = –1
L = {–1; 7}
2. Mathematik-Nachhilfe-Aufgabe: Die Lösungsmenge einer quadratischen Gleichung liegt vor. Stelle die quadratische Gleichung auf. Ziehe hierfür den Satz von Vieta heran.
a) {4; 7}
Bei dem Satz von Vieta gilt Folgendes:
–p = x1 + x2
–p = 4 + 7
–p = 11 | · (–1)
p = –11
q = x1 · x2
q = 4 · 7
q = 28
Die quadratische Gleichung in der Normalform ist hier:
x² – 11x + 28 = 0
b) {–3; 5}
Bei Satz von Vieta gelten folgende Gesetzmäßigkeiten:
–p = x1 + x2
–p = –3 + 5
–p = 2 | · (–1)
p = –2
q = x1 · x2
q = (–3) · 5
q = –15
Die quadratische Gleichung in der Normalform ist:
x² – 2x – 15 = 0
c) {–0,6; –0,4}
Beim Satz von Vieta gilt dieses:
–p = x1 + x2
–p = (–0,6) + (–0,4)
–p = –1 | · (–1)
p = 1
q = x1 · x2
q = (–0,6) · (–0,4)
q = 0,24
Die Normalform der quadratischen Gleichung ist:
x² + x + 0,24 = 0
d)
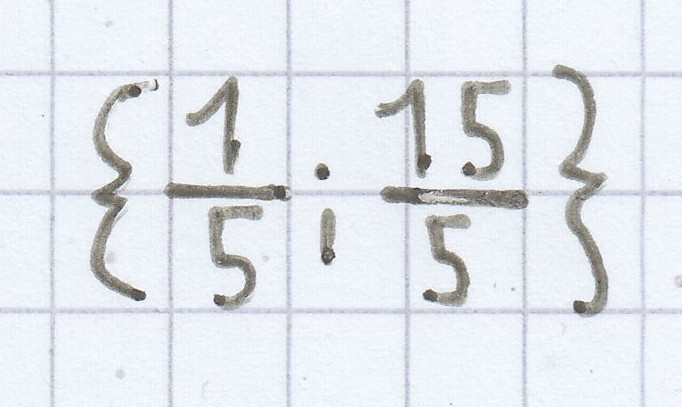
Beim Satz von Vieta gilt Folgendes:
–p = x1 + x2
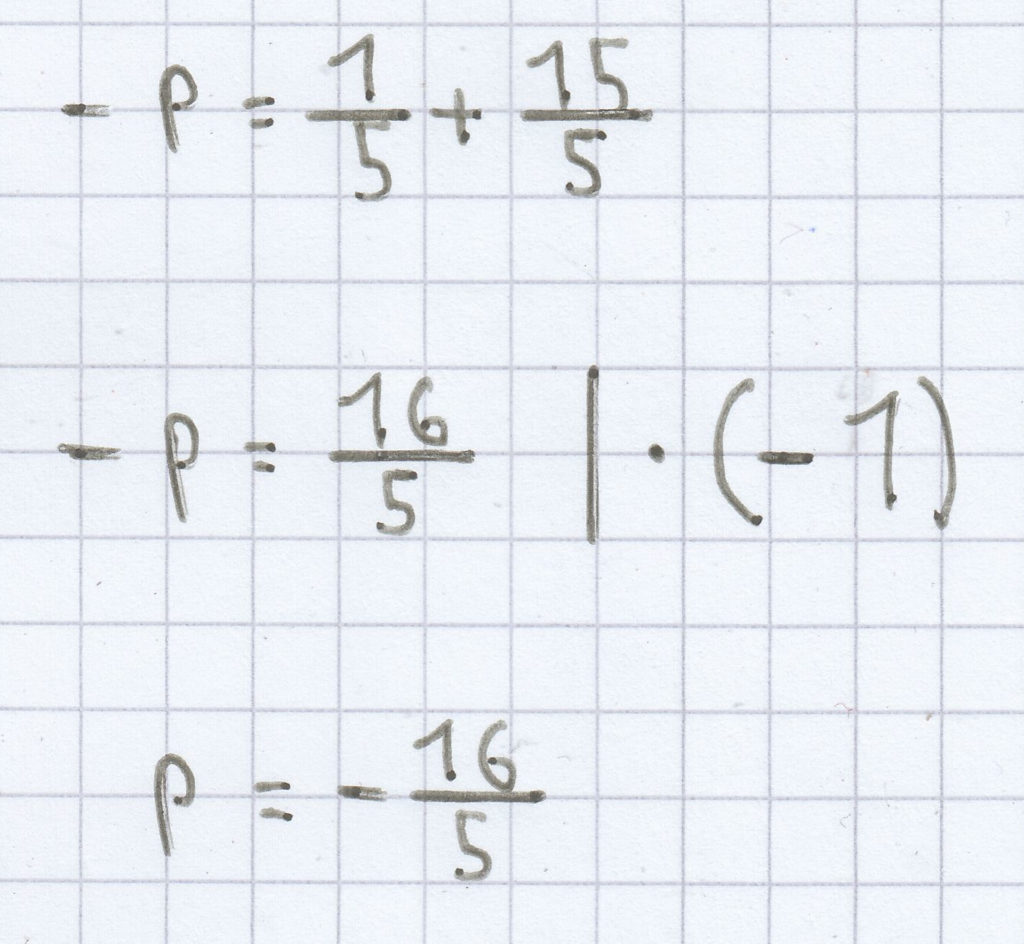
q = x1 · x2
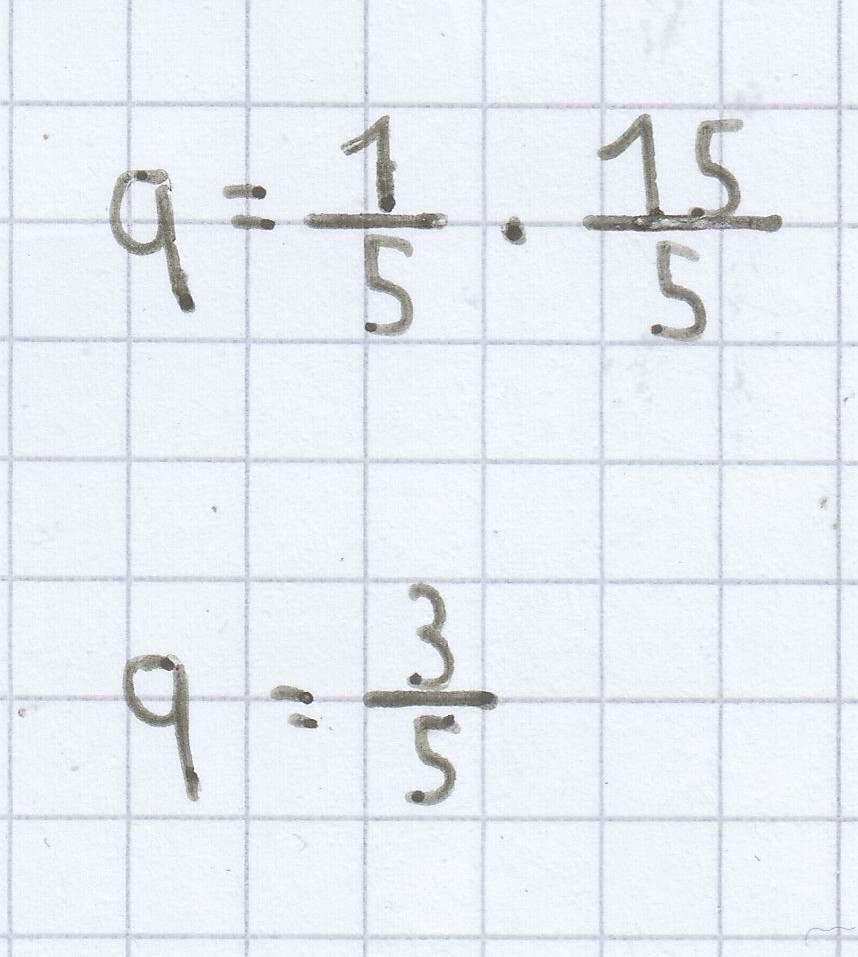
Die quadratische Gleichung hat hier folgende Normalform:
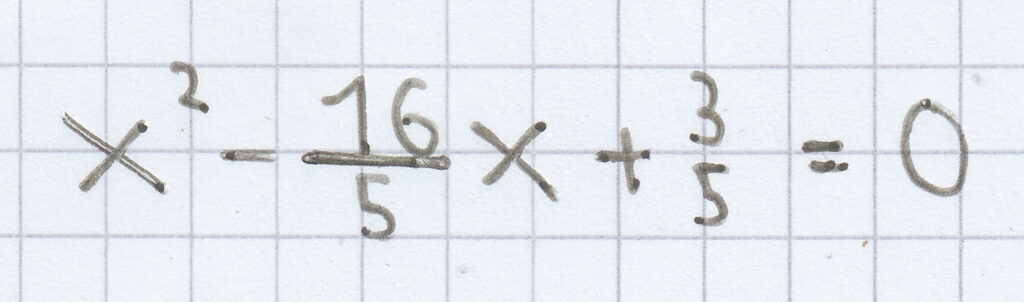
3. Mathe-Nachhilfe-Aufgabe: Überprüfe, ob die Lösungen tatsächlich Lösungen der angegebenen quadratischen Gleichung sind. Falls nicht, ändere die quadratische Gleichung so, dass das der Fall ist.
a) x² + 2x – 24 = 0 L = {4; –6}
–p = x1 + x2
–p = 4 + (–6)
–p = –2 | · (–1)
p = 2
q = x1 · x2
q = 4 · (–6)
q = –24
Die quadratische Gleichung in der Normalform ist:
x² + 2x – 24 = 0
Die angegebene quadratische Gleichung entspricht der hierfür angegebenen Lösung.
b) y² + 3y + 2,25 = 0 L = {–1,5}
–p = y1 + y2
–p = (–1,5) + (–1,5)
–p = –3 | · (–1)
p = 3
q = y1 · y2
q = (–1,5) · (–1,5)
q = 2,25
Es ergibt sich hier folgende quadratische Gleichung in der Normalform:
y² + 3y + 2,25 = 0
Die angegebene quadratische Gleichung ist mit der über den Satz von Vieta ermittelnden identisch.
c) a² + 6a – 16 = 0 L = {–2; 8}
–p = a1 + a2
–p = (–2) + 8
–p = 6 | · (–1)
p = –6
q = a1 · a2
q = (–2) · 8
q = –16
Die quadratische Gleichung in der Normalform ist folgende:
a² – 6a – 16 = 0
Die angegebene Gleichung ist mit der über den Satz von Vieta aufgestellten nicht identisch. Es muss das „6a“ hin zu „–6a“ verändert werden.
d) 4y² + 30y + 56 = 0 L = {–4; –3,5}
Hier muss man erst bei der quadratischen Gleichung deren Normalform ermitteln.
4y² + 30y + 56 = 0 | : 4
y² + 7,5y + 14 = 0
–p = y1 + y2
–p = (–4) + (–3,5)
–p = –7,5 | · (–1)
p = 7,5
q = y1 · y2
q = (–4) · (–3,5)
q = 14
Hieraus ergibt sich diese quadratische Gleichung in der Normalform:
y² + 7,5y + 14 = 0
Die über den Satz von Vieta aufgestellte quadratische Gleichung ist mit der angegebenen Gleichung identisch.
4. Mathematik-Nachhilfe-Aufgabe: Bestimme die Länge und die Breite eines Rechtecks.
Ein Rechteck besitzt einen Flächeninhalt von 30 cm² und einen Umfang von 23 cm. Wie groß sind dessen Längen?
Die Länge und die Breite muss größer null sein, da es sich ja um Längen handelt!
Daher gilt für a, b: a, b > 0
Für den Flächeninhalt eines Rechtecks gilt:
AR = a · b
Hieraus ergibt sich folgende Gleichung:
30 = a · b (1)
Für den Umfang eines Rechtecks gilt:
UR = 2a + 2b
Hieraus ergibt sich diese Gleichung:
23 = 2a + 2b (2)
Die einfachere Gleichung löst man nun nach einer Unbekannten hin auf und setzt diese im Anschluss in die andere Gleichung ein.
30 = a · b | : b
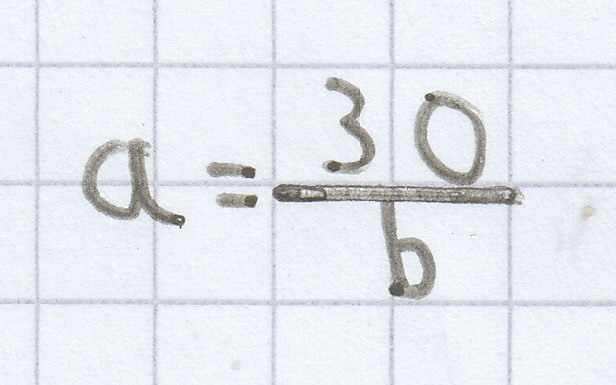
(3)
(3) in (2)
23 = 2 · (${\frac{30}{\mathrm b}}$) + 2b
Diese Gleichung mit jetzt einer Variablen löst man nach der Variablen b hin auf.
23 = ${\frac{60}{\mathrm b}}$ + 2b | · b
23b = 60 + 2b² | – 23b
2b² – 23b + 60 = 0 | : 2
b² – 11,5b + 30 = 0
b1,2 = ${\frac{11,5}{2}$ ± $\sqrt{\ ({\frac{11,5}{2})^2-30}}$
b1,2 = 5,75 ± $\sqrt{\ (33,0625-30)}}$
b1,2 = 5,75 ± $\sqrt{\ 3,0625}}$
b1,2 = 5,75 ± 1,75
b1 = 5,75 + 1,75
b1 = 7,5
b2 = 5,75 – 1,75
b2 = 4
Aus den beiden Lösungen kann man nun a ermitteln:
a1 = ${\frac{30}{7,5}}$
a1 = 4
a2 = ${\frac{30}{4}}$
a2 = 7,5
Da es sich um ein Rechteck handelt, kann die Länge oder die Breite verschieden groß sein, je nachdem, was man als Länge und Breite bezeichnet. Das bestätigt auch die quadratische Gleichung und deren Lösungen sowie das Einsetzen der Lösungen, um die anderen beidenen Lösungen zu erhalten.
Das Rechteck hat (jedenfalls) die Längen 4 cm und 7,5 cm.