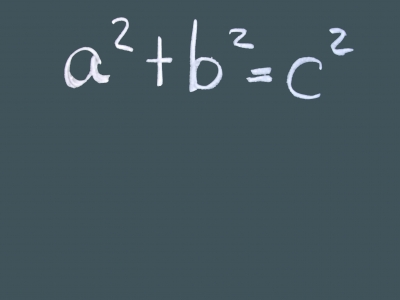
Bei einem rechtwinkligen Dreieck gilt der Satz des Pythagoras. Demzufolge gilt diese sehr berühmte Gesetzmäßigkeit nicht, wenn kein rechtwinkliges Dreieck vorliegt. Ist nun ein rechtwinkliges Dreieck gegeben, dann weist solch ein Dreieck immer eine Hypotenuse und zwei Katheten auf. Was ist aber was? Das ist ganz, ganz einfach – und sollte man deshalb auch nie vergessen. Die Hypotenuse ist immer die Seite im rechtwinkligen Dreieck, die sich gegenüber dem rechten Winkel befindet. Die anderen Seiten sind dann stets die Katheten, da die Hypotenuse ja immer festgelegt ist. Demzufolge ist auch stets klar, wenn man den Satz des Pythagoras an einem beliebigen rechtwinkligen Dreieck aufgestellt, was für eine Gleichung sich ergibt bzw. ergeben muss .
Aufgaben zum Mathe-Stoffgebiet Satz des Pythagoras
1. Mathematik-Nachhilfe-Aufgabe: Stelle zu den abgebildeten Dreiecken jeweils den Satz des Pythagoras auf. Hebe die Hypotenuse grün hervor und die Katheten blau.
2 Mathe-Nachhilfe-Aufgabe: Es ist ein gleichseitiges Dreieck mit dem Umfang U = 12 cm gegeben. Wie groß ist der Flächeinhalt A des Dreiecks?
3. Mathematik-Nachhilfe-Aufgabe: Überprüfe, welche der gegebenen Zahlentripel pythagoreische Zahlentripel sind.
a) (5 | 13 | 12)
b) (12 | 6 | 16)
c) (9 | 12 | 15)
d) (9 | 41 | 40)
4. Mathe-Nachhilfe-Aufgabe: Bei einem Quadrat ist die Seitenlange a = 5 cm. Wie groß ist die Diagonale des Quadrats?

Lösungen zum Mathematik-Stoffgebiet Satz des Pythagoras
1. Mathe-Nachhilfe-Aufgabe: Es soll zu den abgebildeten rechteckigen Dreiecken jeweils der Satz des Pythagoras aufgestellt werden. Die Hypotenuse soll grün und die Katheten blau hervorgehoben werden.
a) Hier ergibt sich folgender Satz des Pythagoras:
a² + c² = b² Rechtwinkliges Dreieck Aufgabe a)
b) Folgender Satz des Pythagoras ergibt sich hier:
a² = b² + c² Rechtwinkliges Dreieck Aufgabe b)
c) Der Satz des Pythagoras ist hier dieser:
n² + p² = o² Rechtwinkliges Dreieck Aufgabe c)
2. Mathematik-Nachhilfe-Aufgabe: Ein gleichseitiges Dreieck hat den Umfang U = 12 cm. Bestimme rechnerisch die Größe des Flächeninhalts.
Der Umfang bei einem gleiseitigen Dreieck ist:
U = a + a + a
U = 3a
Hieraus ergibt sich:
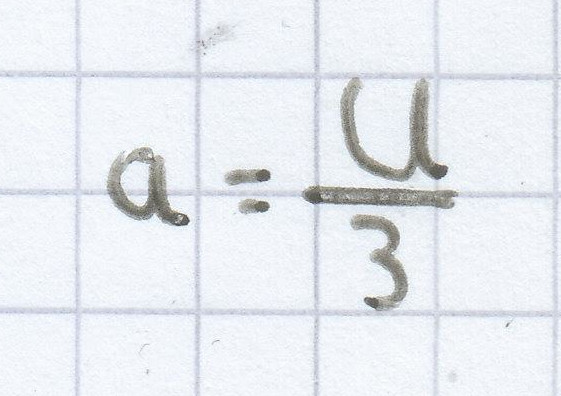
.
Auf das Dreieck bezogen:
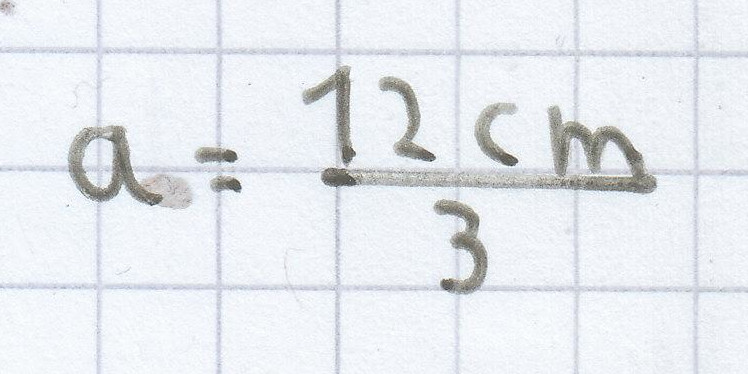
a = 4 cm
Bei einem gleichseitigen Dreieck gilt für den Flächeinhalt Folgendes:
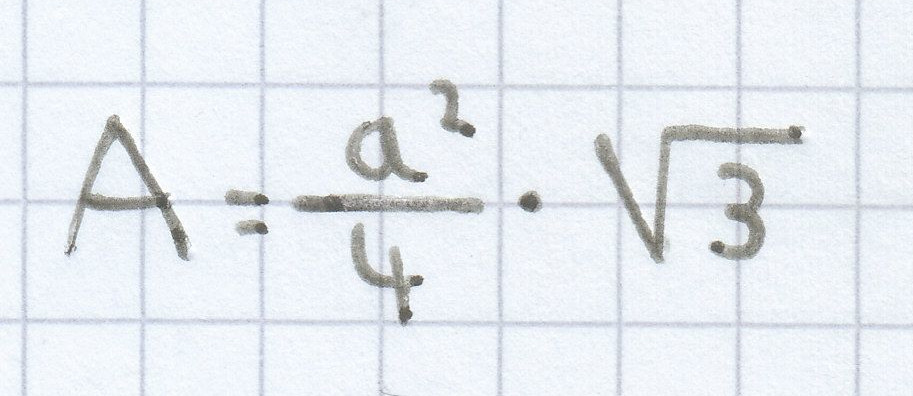
Auf das Dreieck bezogen ergibt sich folgender Flächeninhalt:
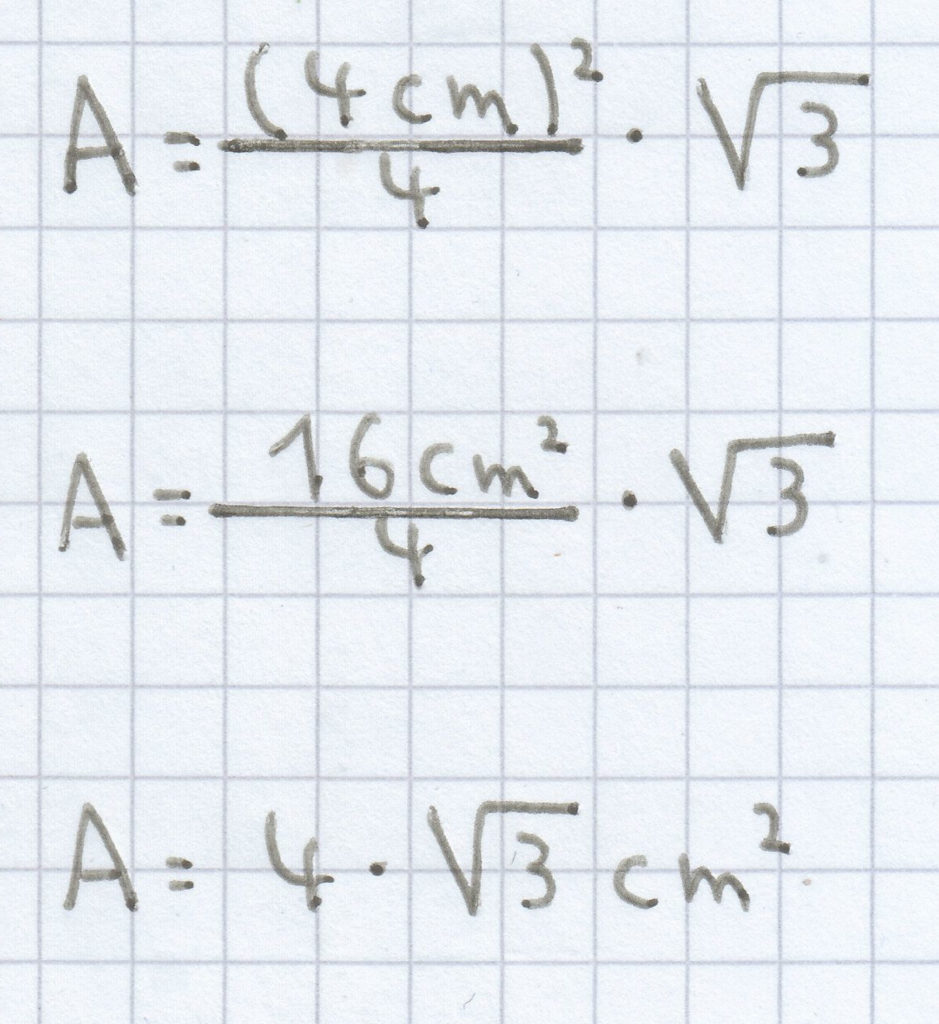
A = 6,93 cm² (gerundet auf zwei Nachkommastellen)
3. Mathe-Nachhilfe-Aufgabe: Welche der angegebenen Zahlentripel sind pythagoreisch?
a)
(5 | 13 | 12)
Ist das Zahlentripel pythagoreisch, dann muss gelten:
(13)² = (5)² + (12)²
169 = 25 + 144
169 = 169
Die Gleichung liefert eine wahre Aussage. Deshalb ist das Zahlentripel pythagoreisch.
b)
(12 | 6 | 16)
(16)² = (6)² + (12)²
256 = 36 + 144
256 = 180
Die Gleichung liefert keine wahre Aussage. Hier liegt daher kein pythagoreisches Zahlentripel vor.
c)
(9 | 12 | 15)
(15)² = (9)² + (12)²
225 = 81 + 144
225 = 225
Die Gleichung ergibt eine wahre Aussage. Hier liegt deshalb ein pythagoreisches Zahlentripel vor.
d)
(9 | 41 | 40)
(41)² = (40)² + (9)²
1681 = 1600 + 81
1681 = 1681
Die Gleichung liefert eine wahre Aussage. Hier liegt daher ein pythagoreisches Zahlentripel vor.
4. Mathematik-Nachhilfe-Aufgabe: Es ist ein Quadrat mit der Seitenlänge a = 5 cm gegeben. Die Diagonale des Quadrats soll mittels des Satz des Pythagoras berechnet werden. Diagonale im Quadrat
Bei einem Quadrat sind alle Seiten gleich lang. Die Diagonale in einem Quadrat bildet mit zwei Seiten ein rechtwinkliges Dreieck. Hierbei sind die Seiten die Katheten und die Diagonale die Hypotenuse. Hieraus ergibt sich dieser Satz des Pythagoras:
d² = a² + a²
d² = 2a² | √
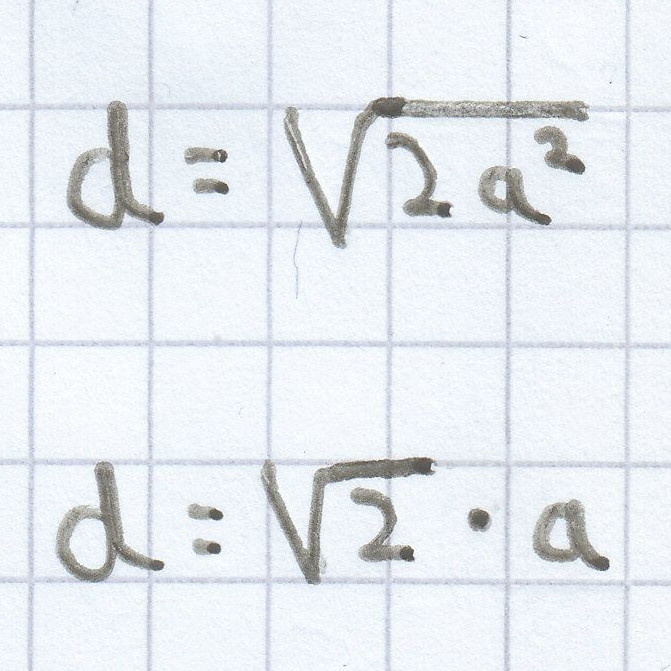
Die Diagonale bei einem Quadrat mit der Seitenlänge 5 cm ist daher:
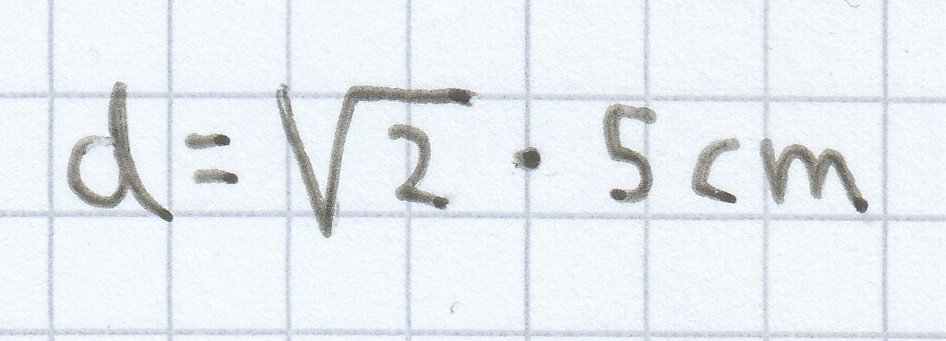
d = 7,07 cm (gerundet auf zwei Nachkommastellen)