1. Lineare Gleichungen und deren Normalform
Die ersten Gleichungen, die man in Mathe lösen muss, sind lineare Gleichungen. Da bei linearen Gleichungen erstmals aufgezeigt wird, mittels welcher algebraischer Umformungen Gleichungen vereinfacht werden und wie man somit die Lösung einer Gleichung ermittelt, bilden diese die Grundlage für das Verständnis aller weiteren in Mathematik folgenden höheren Gleichungen. Daher ist es sehr wichtig, dass jeder Schüler bei linearen Gleichungen möglichst voll und ganz den Durchblick hat.
Lineare Gleichungen bestehen hierbei aus Termen mit einer Variablen, die immer die Potenz hoch 1 vorweist. Hierbei weist solch eine lineare Gleichung stets folgende allgemeine Form auf:
ax + b = 0 (a, b, x ∈ von ℚ oder ℝ (je nach Klassenstufe) und a ≠ 0)
Beispiele für lineare Gleichungen, die in der Normalform stehen:
8x + 8 = 0
2,5 x –10 = 0
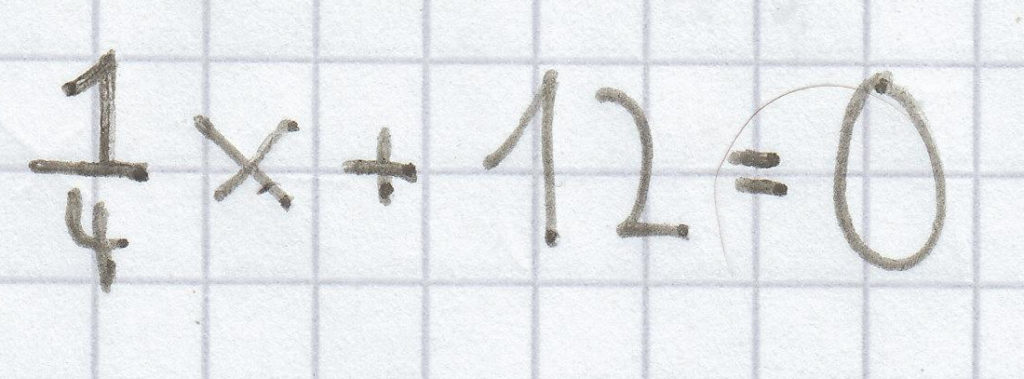
Normalerweise stehen aber lineare Gleichungen nicht in der Normalform, sondern diese weisen rechts und links des Gleichheitszeichens verschiedene Terme auf.
Beispiele für lineare Gleichungen, die nicht in der Normalform stehen (aber durch Äquivalenzumformungen stets in die Normalform gebracht werden können)
4x + 7 = 19
7x + 3x = 12 – 7 + 5x
y + 1 = 8

5,3x + 7 = 9
1 – (x – 1) = 2 – x + 2 (x + 1)
x entspricht x1. In der Mathematik ist es üblich, dass man bei Variablen mit der Potenz hoch 1/„x1“ das „hoch 1“ weglässt und anstelle dessen nur „x“ schreibt.
2. Die verschiedenen Lösungen von linearen Gleichungen
Lineare Gleichungen löst man stets mittels Äquivalenzumformungen, und zwar immer so weit, bis man ein eindeutiges Ergebnis der Gleichung ermittelt hat. Bei linearen Gleichungen können hierbei drei verschiedene Lösungen auftreten. Eine lineare Gleichung kann nämlich entweder genau eine Lösung haben, keine Lösung oder unendlich viele Lösungen haben.
a) Beispiel für eine Lösung einer linearen Gleichung:
8x + 8 = 32 | – 8 <=>
8x = 24 | : 8 <=>
x = 3
L = {3}
Hier ist die einzige Lösung der linearen Gleichung x = 3.
b) Beispiel für keine Lösung einer linearen Gleichung.
5x + 2 = 5x | – 5x <=>
2 = 0
L = { } bzw. L = Ø
Wie man hier sieht, gibt es für die Gleichung keine Lösung. Da sich das x eliminiert hat und die Gleichung stets „unwahr“ ist, existiert für diese Gleichung keine Lösung.
c) Beispiel für unendlich viele Lösungen einer linearen Gleichung
9x + 5 = 12x + 5 – 3x <=>
9x + 5 = 9x + 5 | – 9x <=>
5 = 5 | – 5 <=>
0 = 0
L = ℚ oder ℝ (je nach Klassenstufe)
Da sich bei dieser Gleichung sowohl die Variable als auch die „nackte“ Zahl komplett eliminiert, ist die Gleichung immer „wahr“. Demzufolge gibt es für die Gleichung unendlich viele Lösungen.
Eliminiert sich bei einer linearen Gleichung nur die Variable, so gibt es für die Gleichung immer keine Lösung. Eliminiert sich immer die Variable und die „nackte“ Zahl, dann gibt es immer unendlich viele Lösungen für die Gleichung. Trifft beides beim Umformen einer linearen Gleichung nicht zu, dann liefert die lineare Gleichung immer eine einzige Lösung.