1. Allgemeines zu Strahlensätzen
Bei den Strahlensätzen handelt es sich um ein geometrisches Phänomen, das mit einer Verhältnis-Gleichung wiedergeben werden kann. Damit dies möglich ist, muss Folgendes gewährleistet sein:
Zum einen müssen sich zwei Geraden an einem Punkt schneiden, zum anderen müssen diese beiden Geraden von zwei parallel verlaufenden Geraden geschnitten werden. Liegt dieses geometrische Phänomen vor, so entstehen bei den vier Geraden zwei ähnliche Dreiecke. Innerhalb jener ähnlichen Dreiecke lassen sich nun Streckenverhältnisse in Beziehung bringen – die sogenannten Strahlensätze. Denn die Strecken sind natürlich auch zueinander ähnlich (und unterscheiden sich nur durch einen Faktor k).
Strahlensätze: erste Darstellungsart
Es gilt:

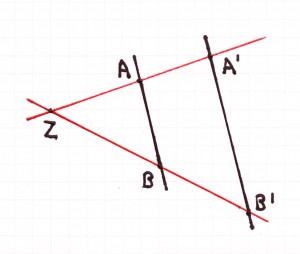
Strahlensätze: zweite Darstellungsart
Es gilt:

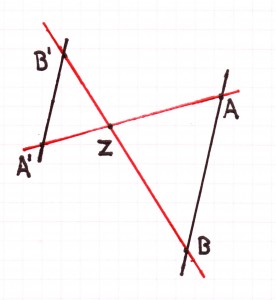
2. Strahlensätze
Immer wenn zwei an einem Punkt sich schneidende Geraden zusätzlich noch von einem Geraden-Parallelpaar geschnitten werden, gelten folgende Gesetzmäßigkeiten:
- Die sich hierdurch ergebenden Strecken der einen Geraden entsprechen den dadurch erzeugten Strecken der anderen Geraden.
Hieraus ergibt sich der 1. Strahlensatz:
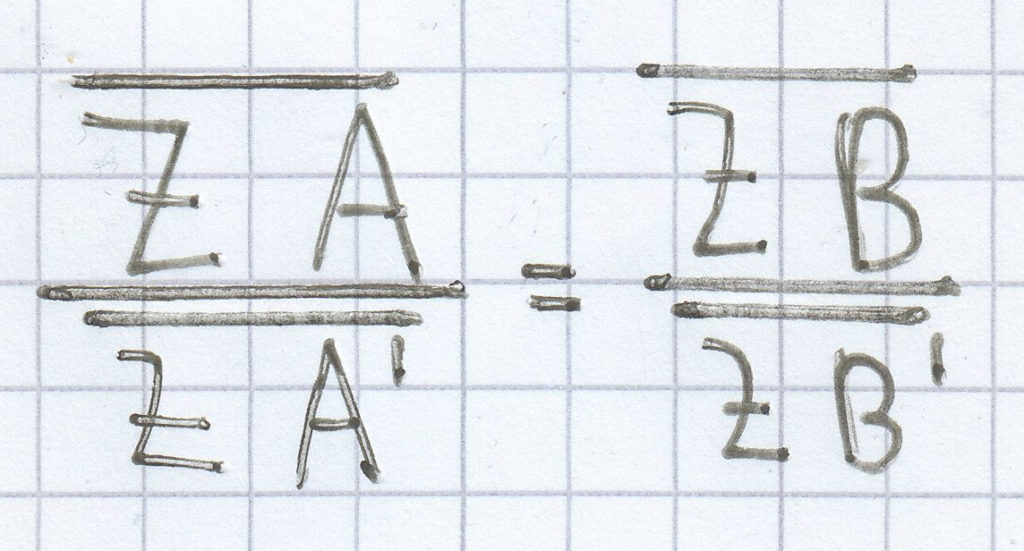
bzw:
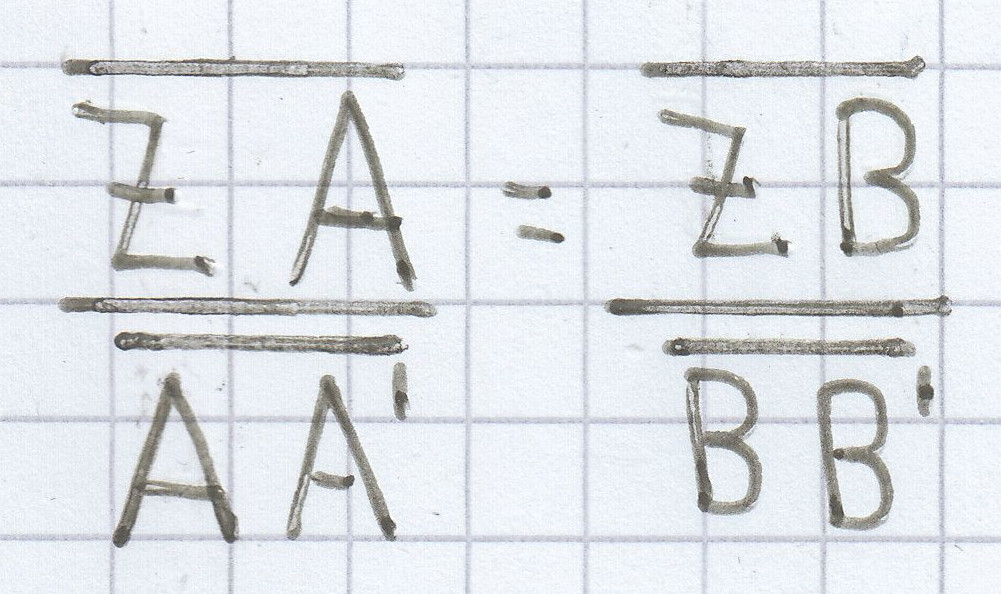
- Die sich hieraus ergebenden parallelen Geraden entsprechen den dadurch erzeugten Strecken auf einer der beiden Geraden.
Hieraus ergibt sich der 2. Strahlensatz:
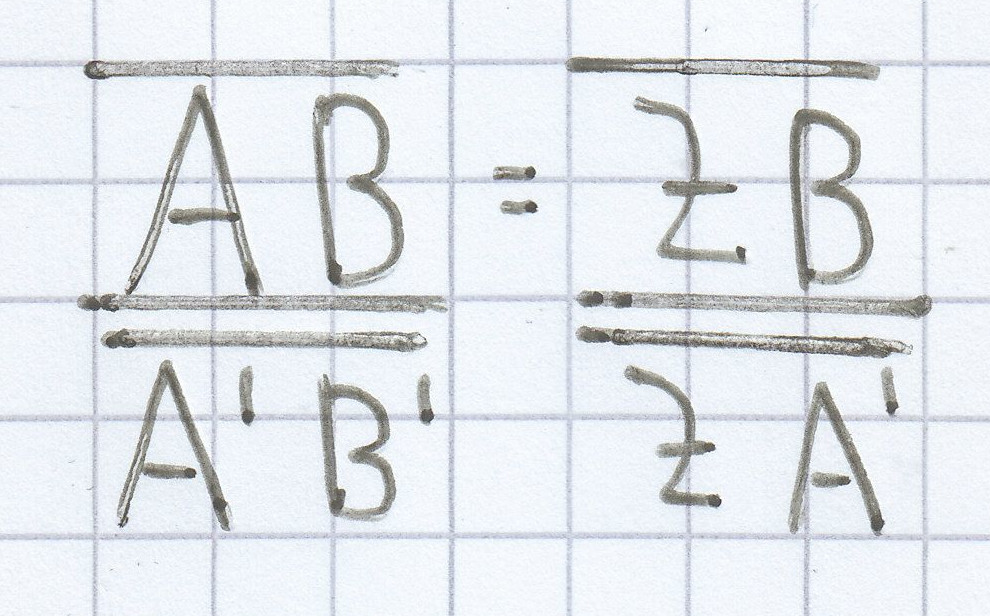
bzw:
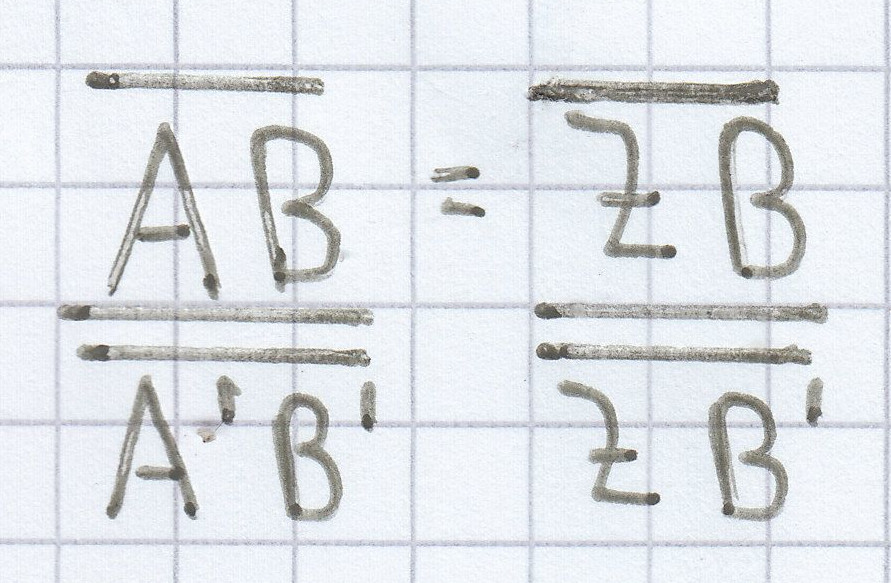
3. Beispiele zu den beiden Strahlensätzen
1. Darstellung der Strahlensätze

Die beiden Strahlensätze sollen nun anhand von folgenden Beispielen auf diese erste Darstellung angewendet werden.
1. Beispiel: Gegeben sind folgende Strecken:

. Berechne mithilfe der Strahlensätze noch diese fehlenden Strecken:
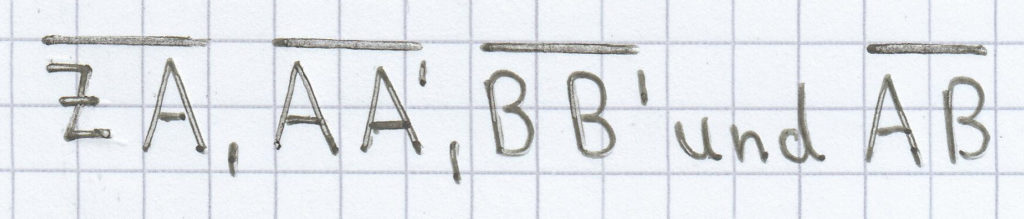
. Zuerst sollte man sich immer genau vor Augen führen, welchen Strecken innerhalb der ähnlichen Dreiecke gegeben sind. Dadurch zeigt sich dann, welche Strecken man mit einem Strahlensatz berechnen kann.
Mit
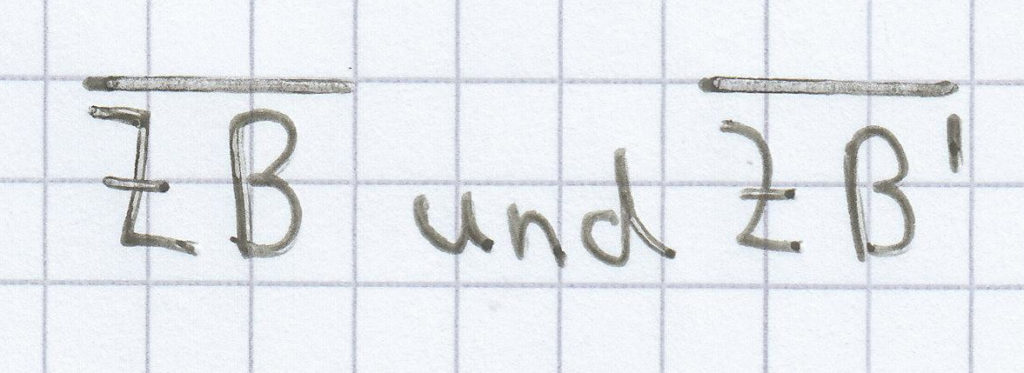
sind bei einer Geraden die kleine und die große Strecke von Z ausgehend gegeben. Da zudem noch die längere Parallele
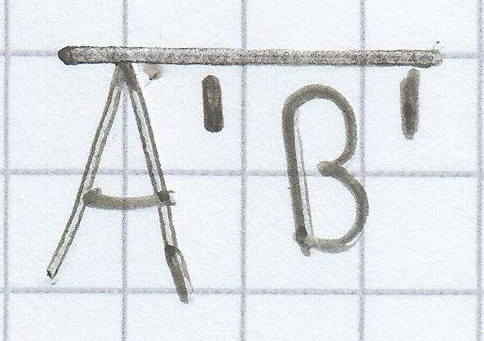
sowie mit

die kürzere Länge der zweiten Geraden gegeben ist, kann man zwei verschiedene Strahlensätze heranziehen.
Beim 1. Strahlensatz
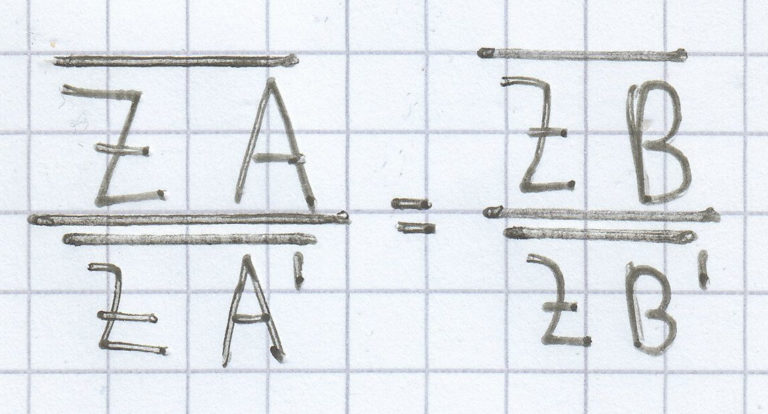
sind alle Streckenlängen bis auf die Streckenlänge
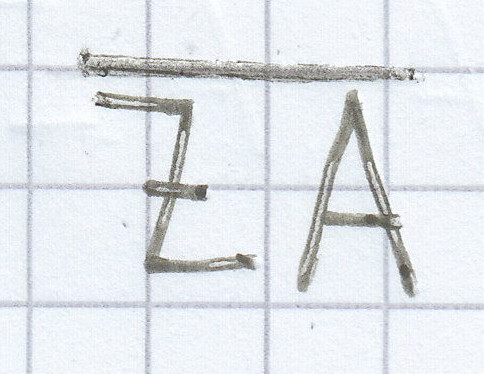
gegeben. Daher kann man die Gleichung sofort nach der gesuchten Strecke hin umstellen.
Da es sich bei den Strahlensätzen jeweils um Gleichungen handelt, kann man mittels Äquivalenzumformungen diese stets zu der gesuchten Strecke hin umformen.
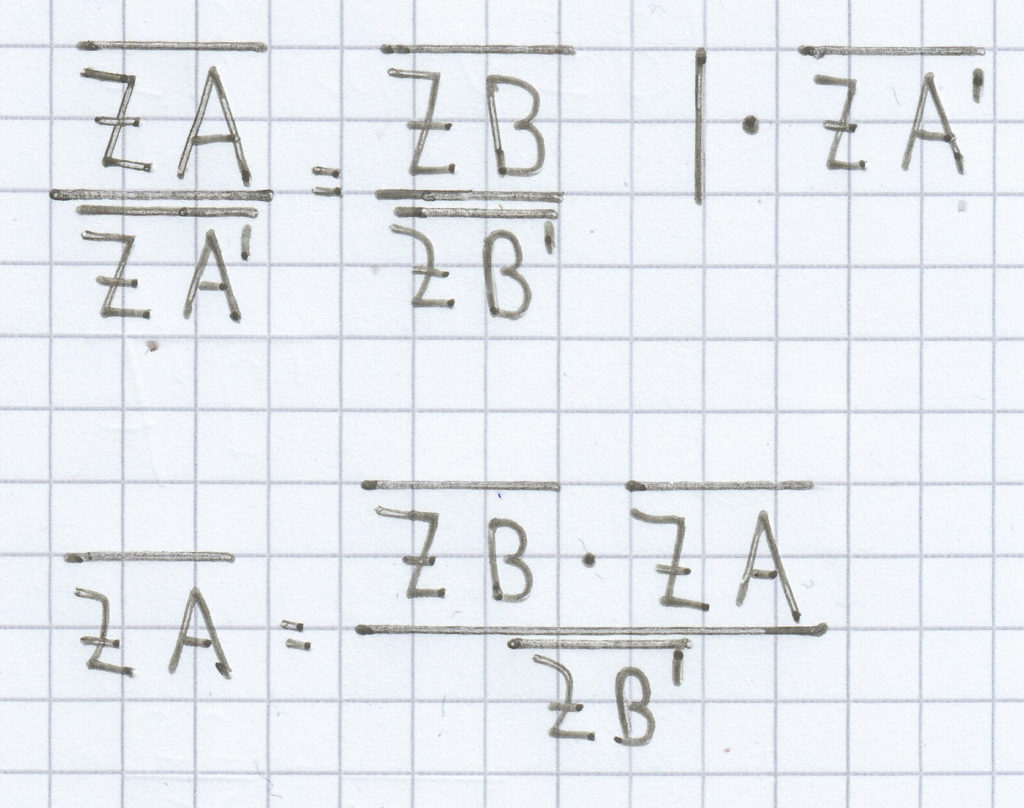
Jetzt kann man die gegebenen Längen einsetzen.
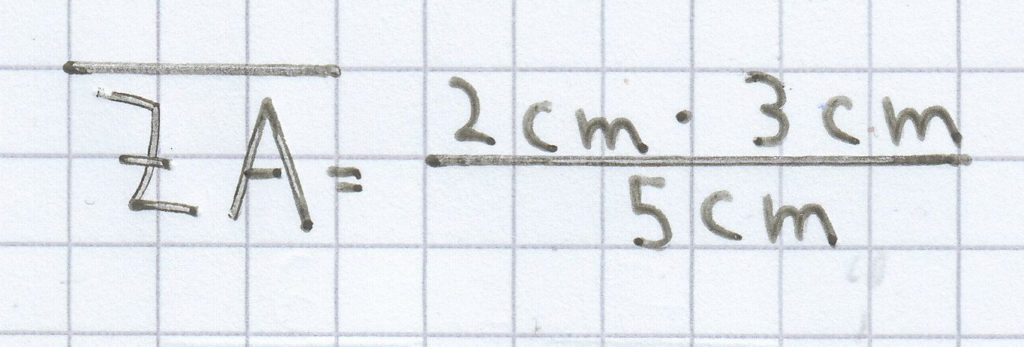
= 1,2 cm
Bei dem 2. Strahlensatz
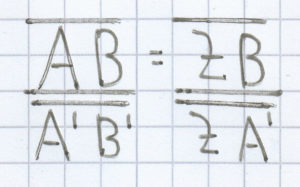
sind ebenso alle Streckenlängen bis auf auf die Länge
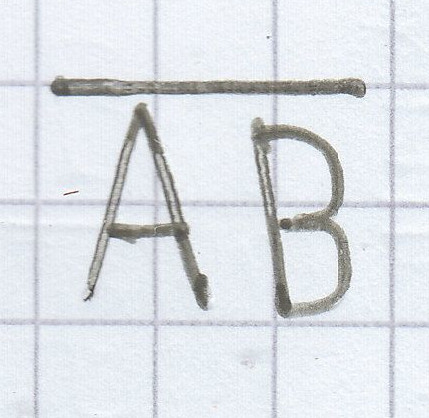
bekannt. Deshalb kann man hier wiederum die Gleichung nach der gesuchten Streckenlänge hin umstellen.
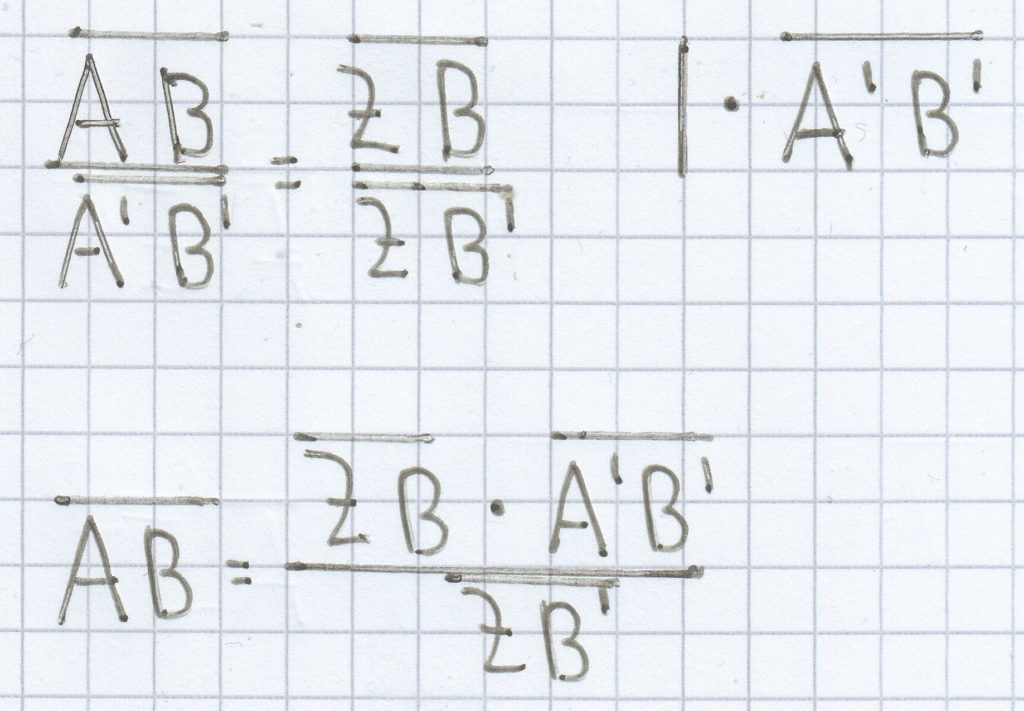
Die gegebenen Werte können daraufhin eingesetzt werden.
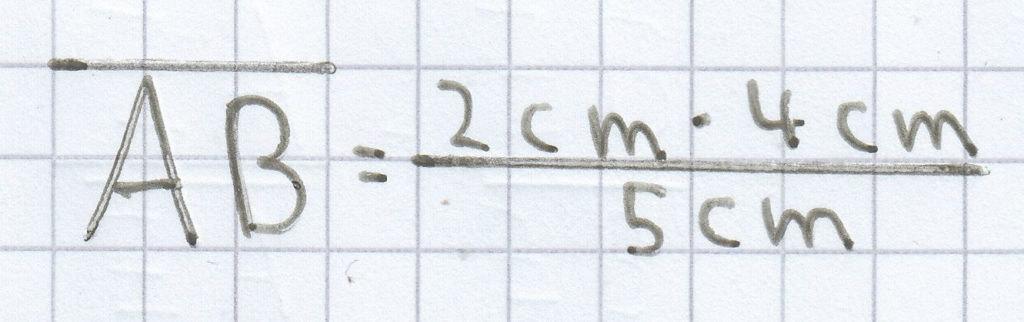
= 1,6 cm
Die Streckenlängen

lassen sich jetzt ganz einfach berechnen. Denn

ist ja nichts anderes als
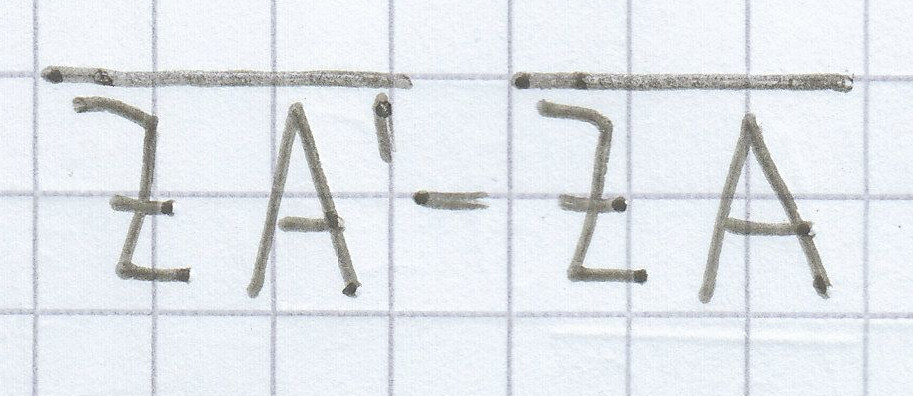
= 3 cm – 1,2 cm
= 1,8 cm
und
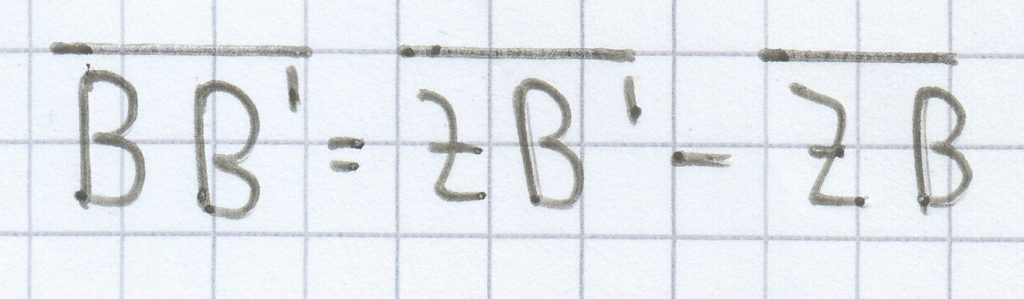
= 5 cm – 3 cm
= 2 cm
2. Darstellung der Strahlensätze

Die 2. Darstellung wird umso einfacher, wenn man das kleine Dreieck gedanklich um 180° in das große Dreieck hineindreht. Dann erhält man nämlich exakt die die 1. Darstellung der Strahlensätze.
2. Beispiel: Gegeben sind die Strecken:
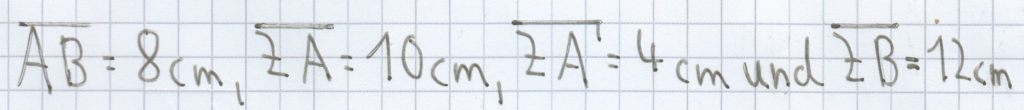
. Berechne mithilfe der Strahlensätze die noch fehlenden Strecken
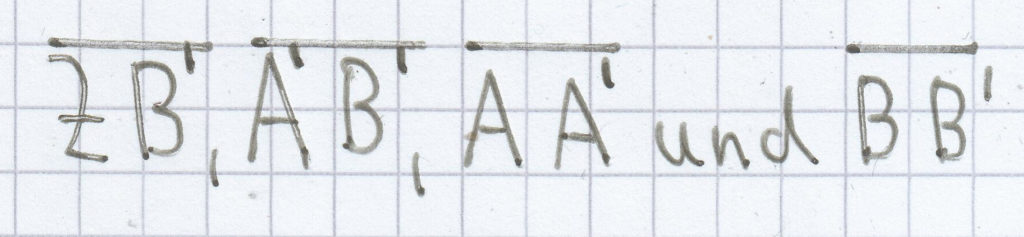
.
Beim 1. Strahlensatz
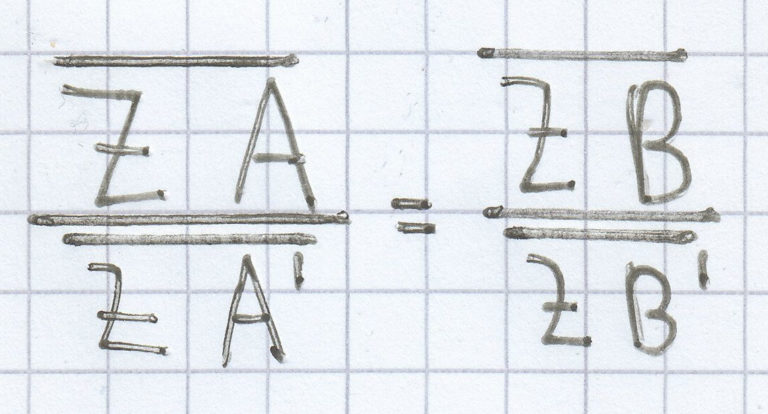
sind bis auf die gesuchte Strecke
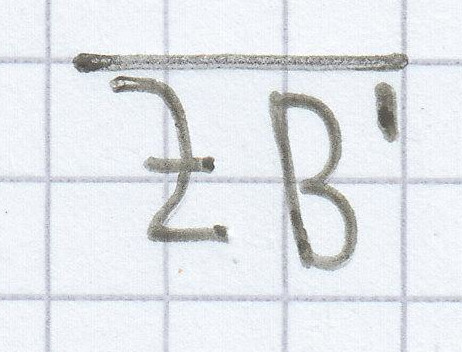
alle Streckenlängen gegeben. Deshalb kann man die Gleichung sofort nach der gesuchten Strecke hin umformen.
Um bei einem Strahlensatz eine gesuchte Strecke, die im Nenner einer der beiden Verhältnisgleichungen sich befindet, schneller separieren zu können, sollte man immer den „doppelten“ Kehrwert an dieser Gleichung anwenden.
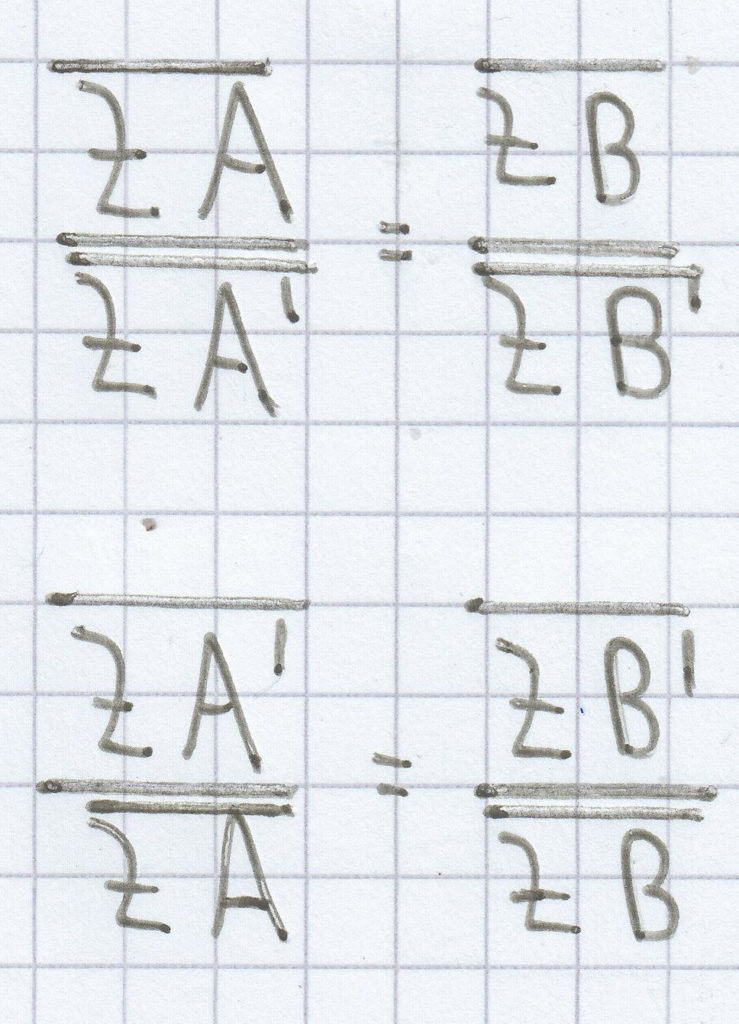
Darauf muss man nur noch eine Äquivalenzumformung durchführen, um die gesuchte Strecke
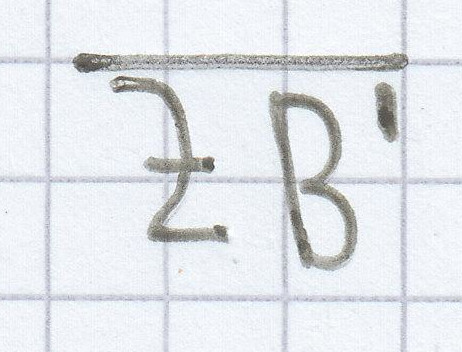
zu separieren.

Die angegebenen Werte kann man nun in die aufgelöste Gleichung einsetzen.

= 4,8 cm
Beim zweiten Strahlensatz sind bis auf die Strecke
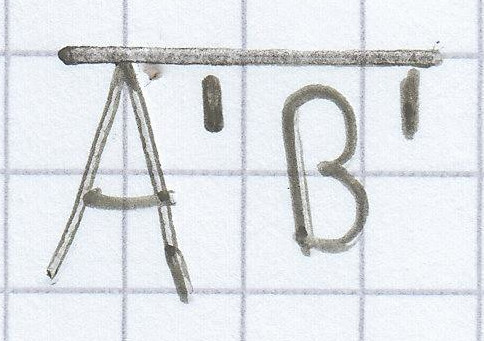
alle Strecken gegeben. Daher kann man diesen sofort nach der noch gesuchten Strecke hin auflösen.
Da sich die gesuchte Strecke im Nenner befindet, macht man als erste Äquivalenzumformung am besten den „doppelten“ Kehrwert.
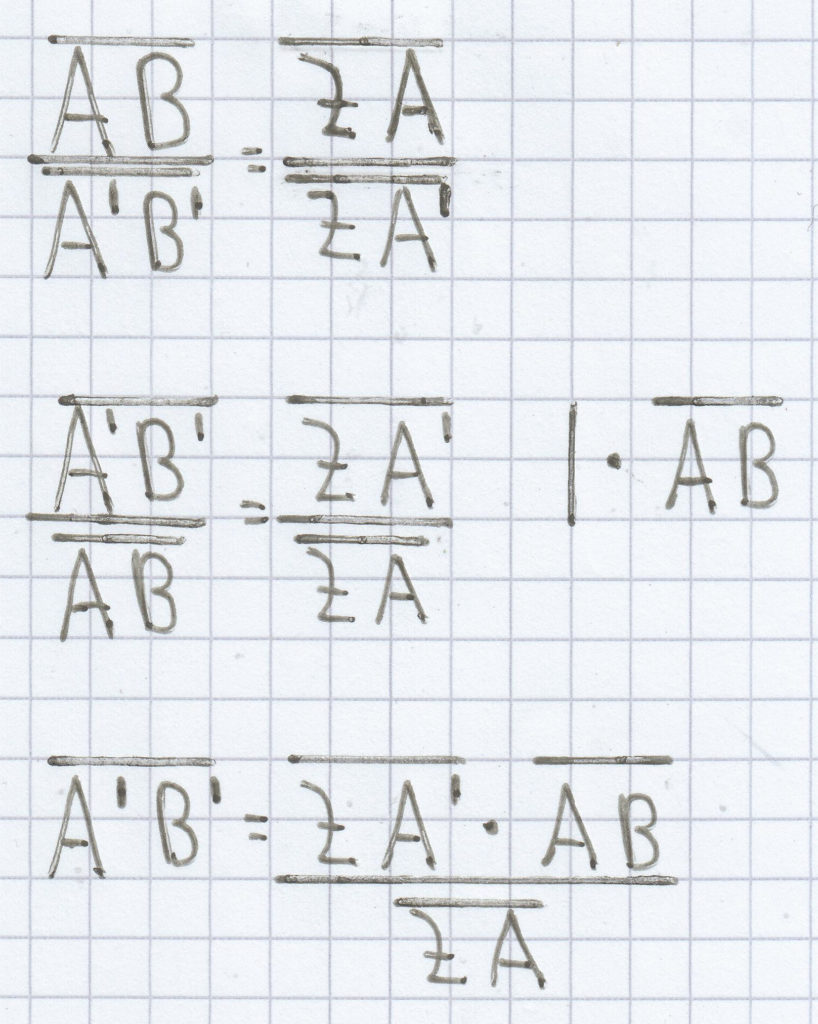
Jetzt kann man die gegebenen Werte in die Gleichung einsetzen.

= 3,2 cm
Die noch gesuchten Streckenlängen

kann man ganz einfach berechnen. Denn die Strecke

= 10 cm + 4 cm = 14 cm.
Die Strecke ist:
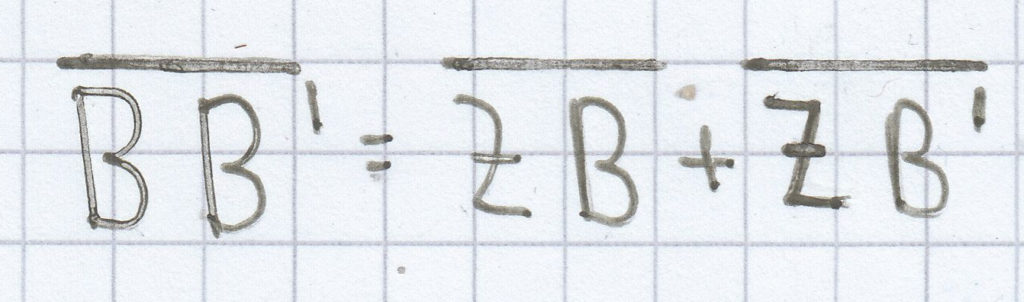
= 12 cm + 4,8 cm = 16,8 cm.