1. Zusammenhang Normalform einer quadratischen Gleichung und deren Lösungen
Liegen bei einer quadratischen Gleichung ihre Lösungen vor, so kann man deren Gleichung in der Normalform ermitteln. Den Lösungsweg hierzu nennt man in Mathe den Satz von Vieta.
Es sind folgende drei quadratische Gleichungen in der Normalform gegeben und deren Lösungen.
a) x² – 9x + 18 = 0 L = {3; 6}
b) x² + 3x – 10 = 0 L = {– 5; 2}
c) x² – 8x + 16 = 0 L = {4}
Aus den Lösungen der quadratischen Gleichungen und deren Normalform kann man eine Gesetzmäßigkeit erkennen.
a) x² – 9 · x + 18 = 0
↓ ↓
(3 + 6) (3 · 6)
b) x² – (–3) · x – 10 = 0
↓ ↓
(–5 + 2) ((–5) · 2)
c) x² – 8 · x + 16 = 0
↓ ↓
(4 + 4) (4 · 4)
Satz: Es liegt eine quadratische Gleichung in der sogenannten Normalform x² + px + q = 0 vor.
Sind x1 und x2 Lösungen dieser quadratischen Gleichung, so ergibt sich folgende Gesetzmäßigkeit:
x1 + x2 = –p und x1 · x2 = q.
Hat die quadratische Gleichung hingegen nur eine Lösung, so ergibt sich diese Gesetzmäßigkeit:
2x1 = –p und x12 = q.
1.1 Beweis des Satzes für zwei Lösungen
1. Fall: Die quadratische Gleichung x² + px + q = 0 weist die Lösungen x1 und x2 auf.
Mittels der Diskriminante

kann die Lösung der quadratischen Gleichung wie folgt bestimmt werden:

Hieraus folgt:
(1)
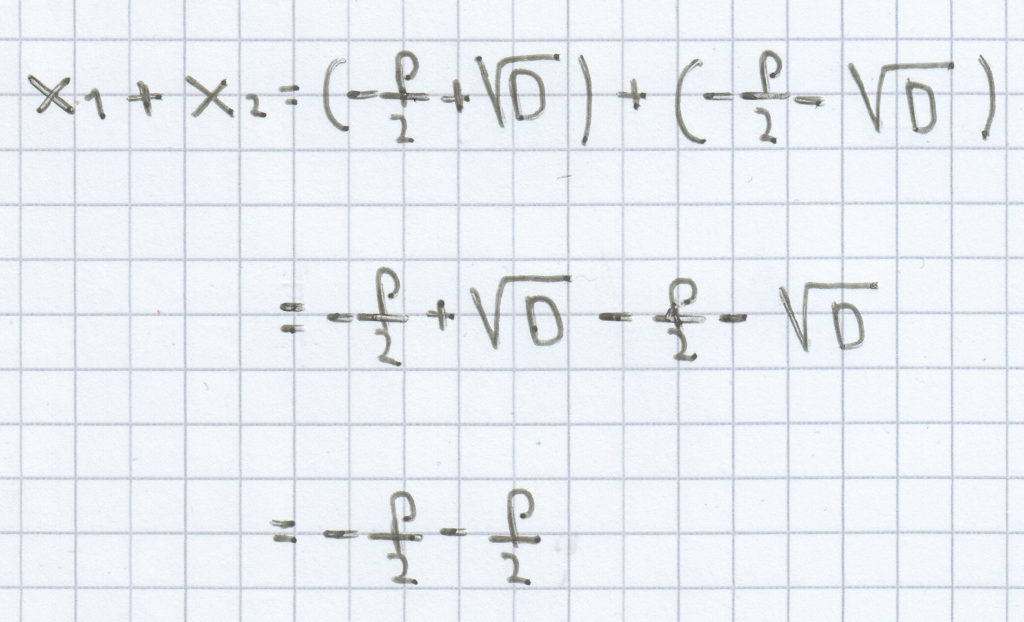
= –p
(2)
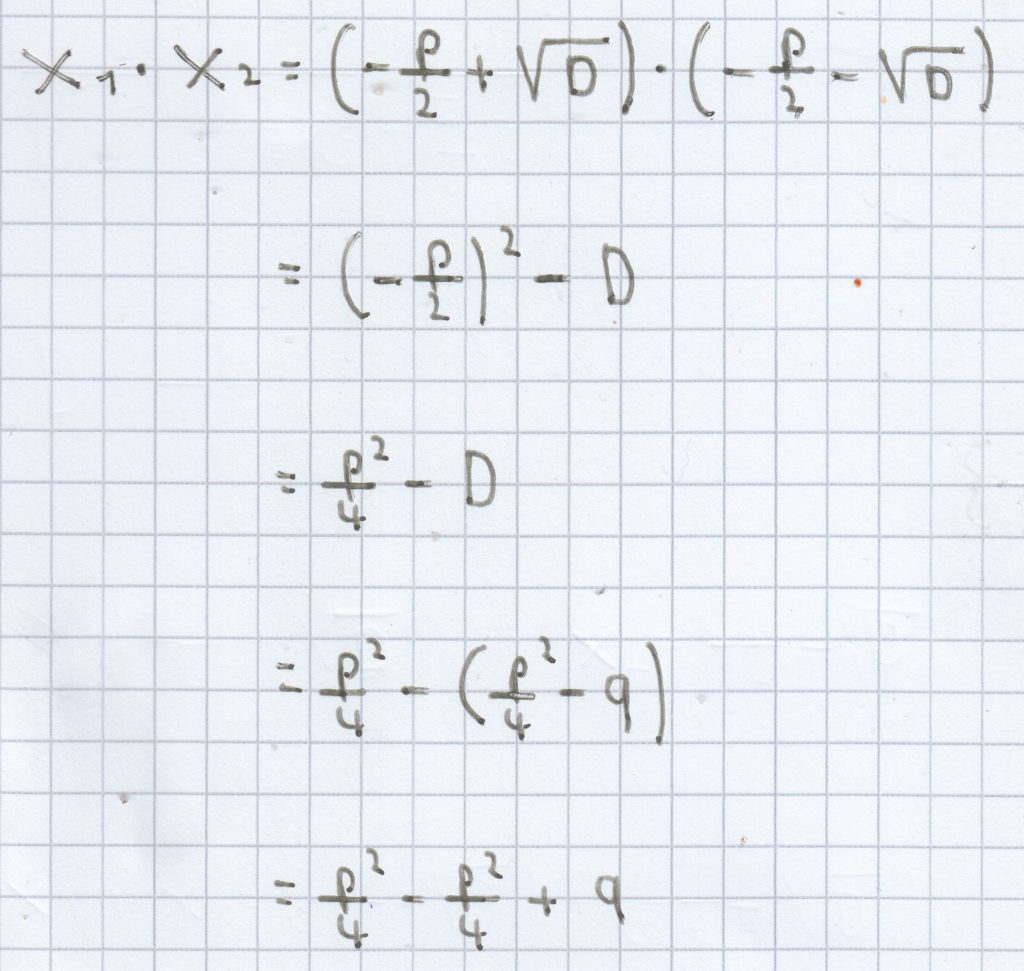
= q
1.2 Beweis des Satzes für eine Lösung
2. Fall: Die quadratische Gleichung x² + px + q = 0 hat nur die eine Lösung x1.
Hat eine quadratische Gleichung nur eine Lösung, so ist deren Diskriminante immer gleich null. Damit die Diskriminante gleich null wird, muss Folgendes gelten:
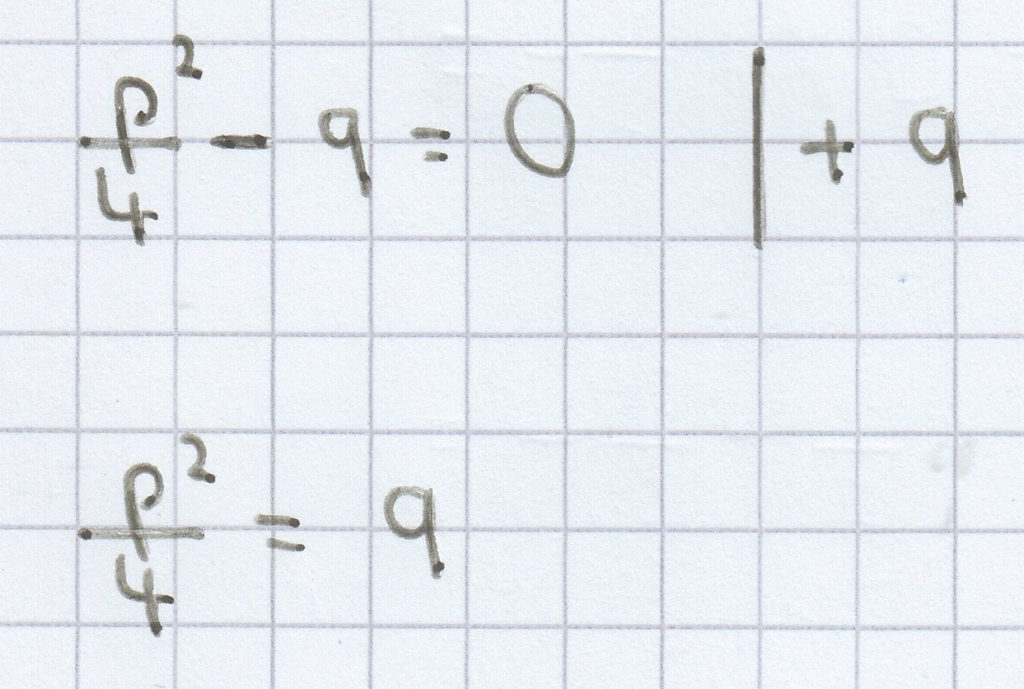
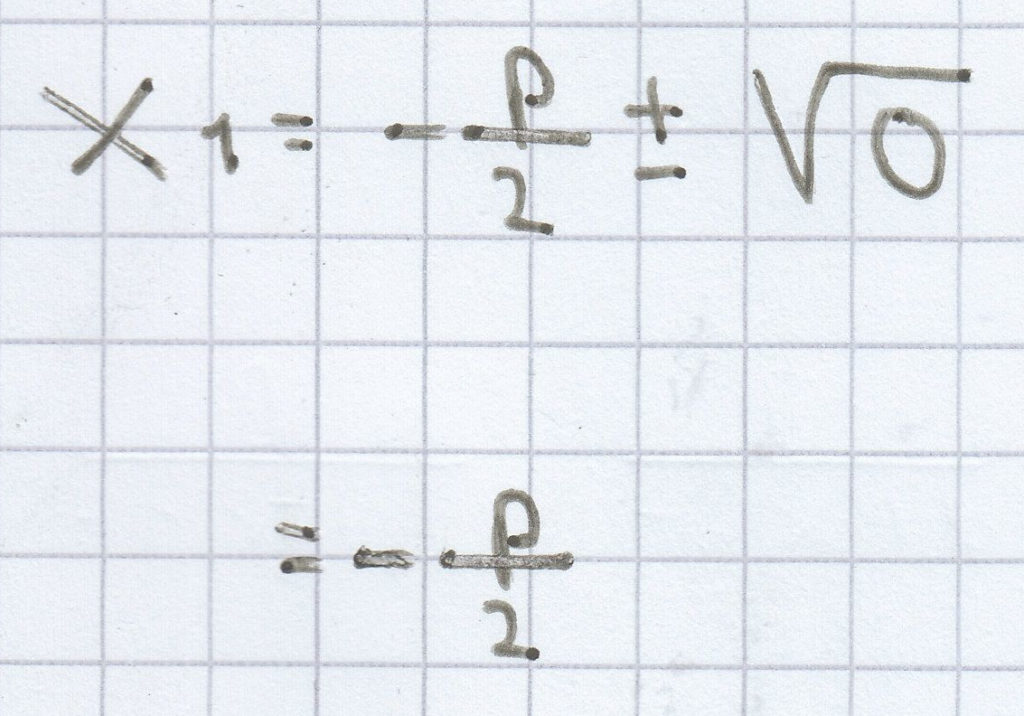
Hieraus folgt:
(1)

= –p
(2)
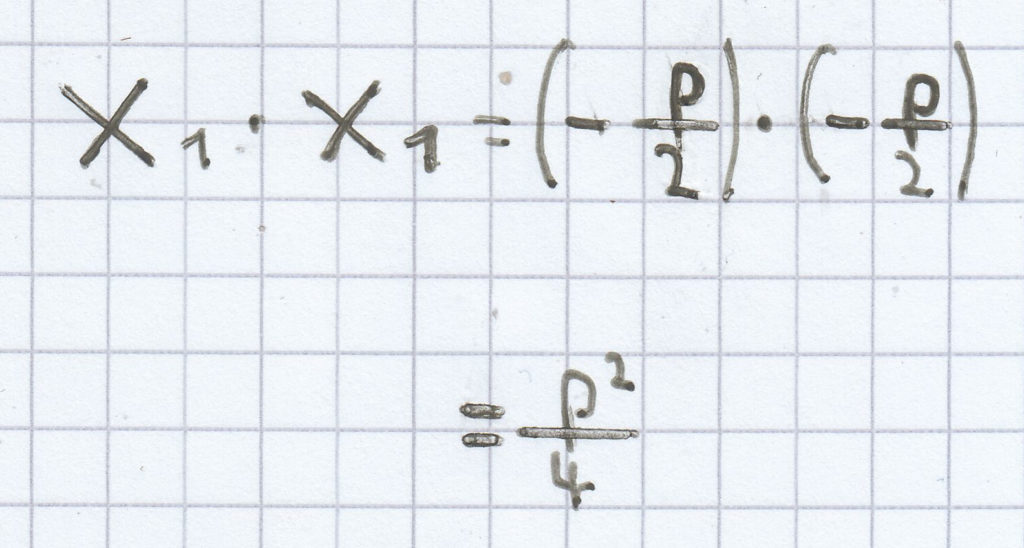
= q
Denn es gilt:

.
1.3 Umkehrung des Satzes
Es ist eine quadratische Gleichung in der Normalform x² + px + q = 0 gegeben. Gilt für zwei Zahlen x1 und x2 dieser Gleichung: x1 + x2 = –p und x1 · x2 = q, so sind x1 und x2 Lösungen jener Gleichung.
1.31 Beweis des Satzes
Sind x1 und x2 Lösungen einer quadratischen Gleichung, so muss gelten:
(x1 + x2) = –p und x1 · x2 = q.
Anhand der Normalform x² + px + q = 0 kann das nun bewiesen werden. Hierfür ist es zuerst notwendig die Normalform zu verändern, indem p und q durch die obige alternative Schreibweise ersetzt werden.
x² – (x1 + x2)x + x1 · x2 = 0.
Um zu zeigen, dass x1 und x2 tatsächlich Lösungen sind, führt man jetzt nacheinander für x1 und für x2 die Probe durch.
Beweis für x1: Probe für x1
x1² – (x1 + x2)x1 + x1 · x2 = 0 (w ?)
x1² – (x1 · x1) – (x2 · x1) + x1 · x2 = 0
x1² – x1² – x1 · x2 + x1 · x2 = 0
0 = 0
Die Probe liefert ein wahres Ergebnis. Damit ist bewiesen, dass x1 eine Lösung der quadratischen Gleichung ist.
Beweis für x2: Probe für x2
x2² – (x1 + x2)x2 + x1 · x2 = 0 (w ?)
x2² – (x1 · x2) – (x2 · x2) + x1 · x2 = 0
x2² – x1 · x2 – x2² + x1 · x2 = 0
0 = 0
Die Probe ergibt ein wahres Ergebnis. Hiermit ist bewiesen, dass x2 eine Lösung der quadratischen Gleichung ist.
2. Der Satz und der Kehrsatz: Satz von Vieta
Es ist eine quadratische Gleichung in der Normalform x² + pq + q = 0 gegeben. Es sind x1 und x2 immer dann Lösungen dieser Gleichung, wenn hierbei gilt: x1 + x2 = –p und x1 · x2 = q.
Diese Gesetzmäßigkeit bei quadratischen Gleichungen nennt man den Satz von Vieta.
Beispiele:
1. Mithilfe des Satzes von Vieta soll für diese allgemeine quadratische Gleichung: x² + px + q = 0 eine quadratische Gleichung ermittelt werden, deren Lösungsmenge ist:
a) {4; 7}
–p = x1 + x2
–p = 4 + 7
–p = 11
q = x1 · x2
q = 4 · 7
q = 28
Die quadratische Gleichung ist: x² – 11x + 28 = 0