
Der kleinste Grundbaustein einer Gleichung und einer Funktion ist ein Term. Gleichungen und Funktionen bestehen daher immer aus Termen bzw. aus Einzeltermen. Hierbei weist ein Term normalerweise immer eine Variable auf. Aber das ist nicht ein absolutes Muss. Ein Term kann auch keine Variable vorweisen, sprich eine „nackte“ Zahl sein. Bei einer Gleichung oder einer Funktion sind die Einzelterme stets mittels sinnvollen Rechenzeichen miteinander verbunden. Terme innerhalb einer Gleichung oder einer Funktion können daher mit einem „+“ mit einem „–“ oder mit einem „·“ oder auch mit einem „:“ (üblicherweise steht in Mathe statt einem „:“ eher ein Bruch) miteinander verbunden sein. Aber auch andere Mathematik-Symbole wie ein „²“ oder einer „√“ oder einem „|4|“ (und noch jede Menge andere) können hier auftreten – solange die Verknüpfung aus der Logik der Mathematik sinnvoll ist!
Aufgaben zum Mathe-Stoffgebiet Terme
1. Mathematik-Nachhilfe-Aufgabe: Was für eine Term liegt vor? Ermittle das Ergebnis der Terme.
a) 7 + 2 · 8 – 2
b) 7 + 2 · (8 – 2)
c) (7 + 2) · 8 – 2
d) (7 + 2) · (8 – 2)
2. Mathe-Nachhilfe-Aufgabe: Berechne das Ergebnis des Terms.
a) (–4)4
b)
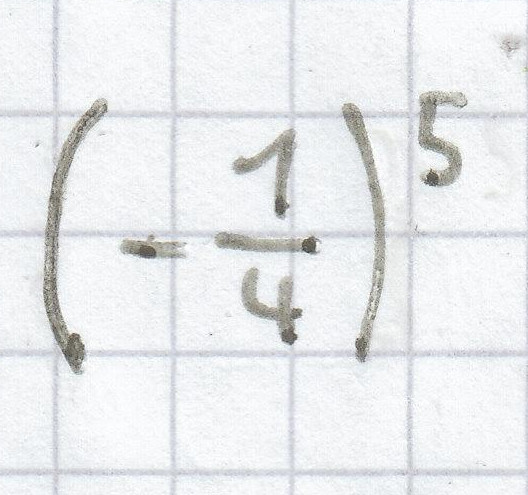
c) 44
d) 410
e) (–5)3
f) –(5)3
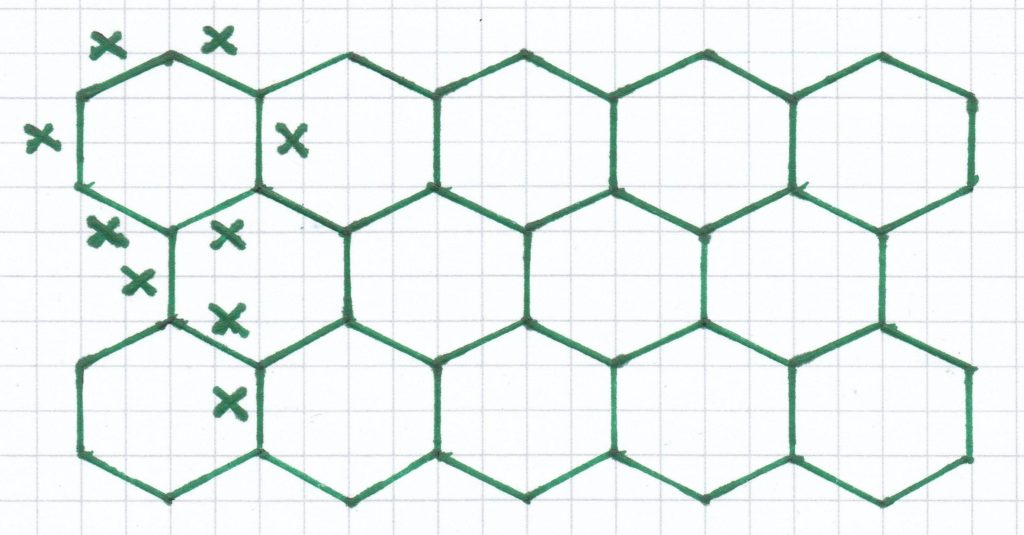
3. Mathematik-Nachhilfe-Aufgabe: Ein Gitternetz soll aus Draht hergestellt werden. Stelle für das abgebildete Gitternetz zwei Terme aus. Berechne die Drahtlänge für x = 5; x = 14 und x = 27 (jeweils in cm).
4. Mathe-Nachhilfe-Aufgabe: Berechne den Wert des Terms. Der Term ist (a – b) · c + d
a) a = 2; b = 4; c = 1; d = 3
b) a = 1; b = –9; c = 0; d = 0
c) a = 0,4; b = 0,4; c = –1; d = 0,5
d) a = –5; b = –11; c = –13; d = –2

Lösungen zum Mathematik-Stoffgebiet Terme
1. Mathe-Nachhilfe-Aufgabe: Was für ein Typ eines Terms liegt vor. Berechne das Ergebnis.
a)
7 + 2 · 8 – 2 =
7 + 16 – 2 =
21
Hier liegt als Typ eine algebraische Summe vor.
Die Rechenoperation die zuletzt bei einem Term durchgeführt wird, bestimmt dessen Typ.
b)
7 + 2 · (8 – 2) =
7 + 2 · (6) =
7 + 12 =
19
Hier ist der Typ des Terms eine Summe.
c)
(7 + 2) · 8 – 2 =
(9) · 8 – 2 =
72 – 2 =
70
Hier ist der Term-Typ eine Differenz.
d)
(7 + 2) · (8 – 2) =
(9) · (6) =
54
Hier ist der Tpy des Terms ein Produkt.
2. Mathematik-Nachhilfe-Aufgabe: Was ist das Ergebnis des Terms?
a) (–4)4 = (–4) · (–4) · (–4) · (–4) = 256
b)
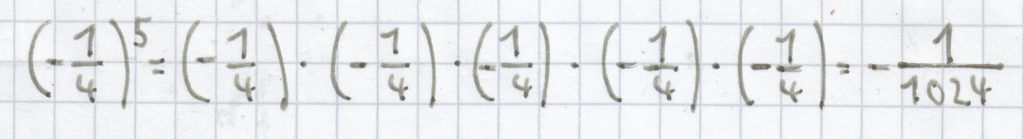
c) 44 = 4 · 4 · 4 · 4 = 256
d) 410 = 4 · 4 · 4 · 4 · 4 · 4 · 4 · 4 · 4 · 4 = 1048576
e) (–5)3 = (–5) · (–5) · (–5) = –125
f) –(5)3 = –(5 · 5 · 5) = –125
3. Mathe-Nachhilfe-Aufgabe: Es soll aus Draht ein Gitternetz hergestellt werden. Für das hier abgebildete Gitternetz sollen 2 verschiedene Terme aufgestellt werden. Berechne die benötigte Drahtänge für x = 5; x = 14 und x = 27 (jeweils in cm).

Ein Term ist: x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x + x
Ein anderer Term ist: 57 · x bzw. 57x
Es ist hier sinnvoll den Term zusammenzufassen, da der Term aus vielen x sehr lang ist. Die benötigte Drahtlänge kann man mittels einer Gleichung wiedergegben: Drahtlänge = 57x.
Bei x = 5 ist die Drahtlänge (57 · 5 = 285) 285 cm.
Bei x = 14 ist die Drahtlänge (57 · 14 = 798) 789 cm.
Bei x = 27 ist die Drahtlänge (57 · 27 = 1539 cm) 1539 cm.
4. Mathematik-Nachhilfe-Aufgabe: Der Wert des Terms soll berechnet werden. Der Term ist (a – b) · c + d.
a)
a = 2; b = 4; c = 1; d = 3
(2 – 4) · 1 + 3 =
(–2) · 1 + 3 =
–2 + 3 =
1
b)
a = 1; b = –9; c = 0; d = 0
(1 – (–9)) · 0 + 0 =
(10) · 0 + 0 =
0
c)
a = 0,4; b = 0,4; c = –1; d = 0,5
(0,4 – 0,4) · (–1) + 0,5 =
(0) · (–1) + 0,5 =
0 + 0,5 =
0,5
d)
a = –5; b = –11; c = –13; d = –2
(–5 – (–11)) · (–13) + (–2) =
(6) · (–13) + (–2) =
–78 + (–2) =
–80