
In Mathe ist die Bedeutung von Wörtern zentral, das führt man sich aber nicht immer bewusst vor Augen (wie das übrigens auch oft im realen Leben der Fall ist). Bei der Einführung von Gleichungen bzw. linearen Gleichungen (was ja die ersten im Fach Mathematik sind), bezieht sich die Bedeutung des Wortes auf die Terme rechts und links des Gleichheitszeichens („=“). Sind nämlich hierbei beide Terme gleich, also rechts und links des Gleichheitszeichens, dann ist die Gleichung auch wahr (formal gesehen). 1 = 1 oder 25 = 25 ist ja beispielsweise nichts anderes als eine wahre Aussage. Sind die Terme jedoch nicht gleich, so liefert die Gleichung eine unwahre Aussage (formal gesehen), wie zum Beispiel: 1 ≠ 2 bzw. 25 ≠ 26.
Aufgaben zum Mathe-Stoffgebiet Lineare Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Welche Zahl liefert für die Gleichung eine wahre Aussage?
a) 3 · (x + 4) = 15
b) (x – 5) 4 = 20
c) (x + 7) : 5 = 0
d) (5x – 3) : 6 = 2
2. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Gleichung.
a) 49 – 11x = 5
b) –4,4 + x = –6,3
c) –4,4a + 0,8a = –2,1
d) –4b – 2,2 = 9
3. Mathematik-Nachhilfe-Aufgabe: Welche Zahl erfüllt das Zahlenrätsel?
a) Addiert man zum 10-Fachen einer Zahl das 9-Fache dieser Zahl, so ergibt sich das 5-Fache dieser Zahl, veringert um 7.
b) Verringert man das Doppelte einer Zahl um 2,5 und nimmt die Differenz mit –2 mal, dann erhält man dasselbe, wenn man die gesuchte Zahl mit dem Faktor 6 multipliziert.
c) Addiert man zur Hälfte einer Zahl das 3-Fache der Zahl, dann ergibt sich das Doppelte der Zahl, verringert um 3.
4. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der linearen Gleichung.
a) –5 + 4x + 12 = –3x – 8 – 7x
b) 2,1y + 19,4 – 2,8y = 4,7y – 1,1 + 0,7y
c) 16a – 0,89 = –48a + 0,31 + 56a
d) 15 – 0,2s + 4 = –1,2s – 21 + 3s

Lösungen zum Mathematik-Stoffgebiet Lineare Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der linearen Gleichung.
a)
3 · (x + 4) = 15
3x + 12 = 15 | – 12
3x = 3 | : 3
x = 1
L = {1}
b)
(x – 5) 4 = 20
4x – 20 = 20 | + 20
4x = 40 | : 4
x = 10
L = {10}
c)
(x + 7) : 5 = 0 | · 5
x + 7 = 0 | – 7
x = –7
L = {–7}
d)
(5x – 3) : 6 = 2 | · 6
5x – 3 = 12 | + 3
5x = 15 | : 5
x = 3
L = {3}
2. Mathematik-Nachhilfe-Aufgabe: Welche Zahl liefert bei der Gleichung eine wahre Aussage?
a)
49 – 11x = 5 | – 49
–11x = –44 | : (–11)
x = 4
L = {4}
b)
–4,4 + x = –6,3 | + 4,4
x = –1,9
L = {–1,9}
c)
–4,4a + 0,8a = –2,1
–3,6a = –2,1 | : (–3,6)
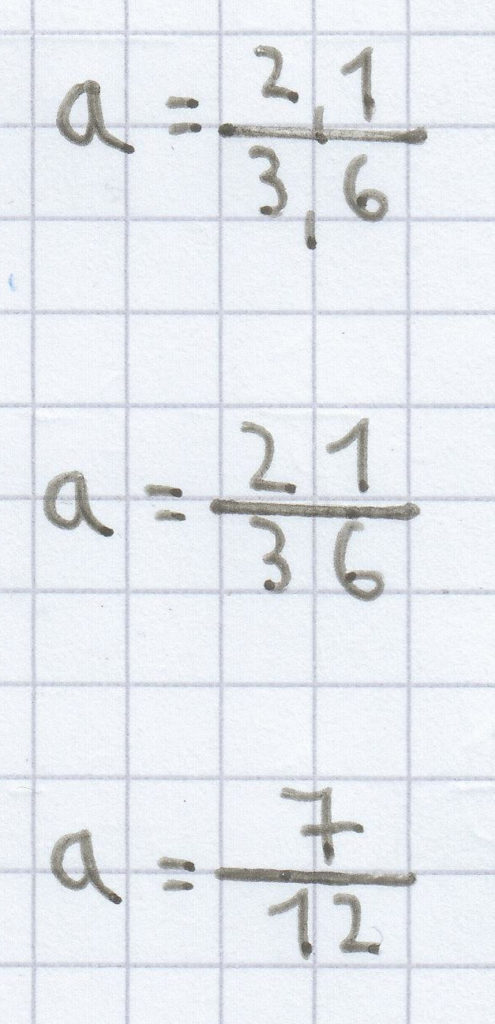
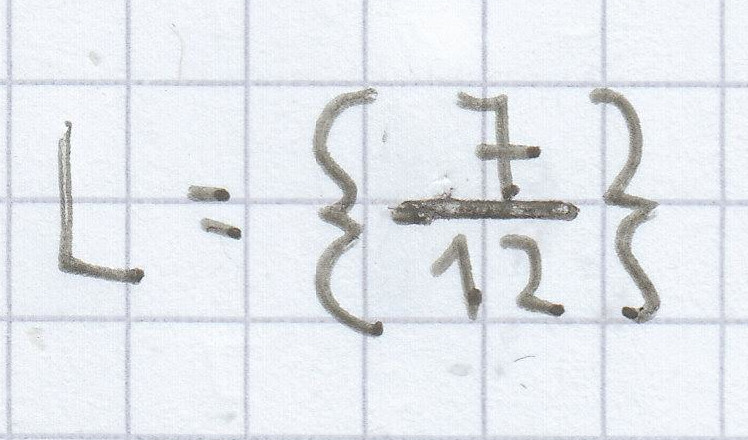
d)
–4b – 2,2 = 9 | + 2,2
–4b = 11,2 | : (–4)
b = –2,8
L = {–2,8}
3. Mathe-Nachhilfe-Aufgabe: Ermittle die gesuchte Zahl des Zahlenrätsels.
a) Wenn man das 10-Fache einer Zahl um das 9-Fache der Zahl erhöht, so erhält man das 5-Fache der Zahl, verkleinert um 7.
Bei der Aufstellung der Gleichung ist es immer sehr wichtig, dass der Term rechts und links der Gleichung korrekt ist – ansonsten erhält man ja ein falsches Ergebnis!
10x + 9x = 5x – 7
19x = 5x – 7 | – 5x
14x = –7 | : 14
x = –0,5
L = {–0,5}
Die gesuchte Zahl ist –0,5.
b) Wenn man das Doppelte einer Zahl um 2,5 verringert und die Differenz mit dem Faktor –2 malnimmt, so erhält man dassselbe, wenn man die gesuchte Zahl mit dem Faktor 6 malnimmt.
(2x – 2,5) · (–2) = 6x
–4x + 5 = 6x | + 4x
5 = 10x | : 10
x = 0,5
L = {0,5}
Die gesuchte Zahl des Zahlenrätsels ist 0,5.
c) Wenn man zur Hälfte einer Zahl deren 3-Faches hinzuaddiert, so erhält man das Doppelte der Zahl, verringert um 3.
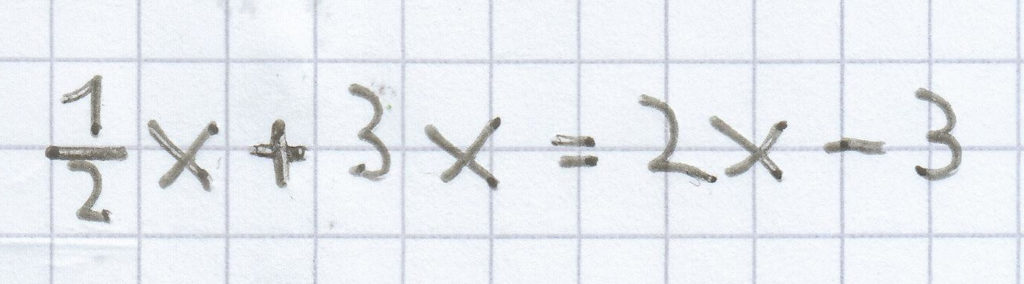
3,5x = 2x – 3 | – 2x
1,5x = –3 | : 1,5
x = –2
L = {–2}
Die gesuchte Zahl ist –2.
4. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der linearen Gleichung.
a)
–5 + 4x + 12 = –3x – 8 – 7x
7 + 4x = –10x – 8 | + 10x
7 + 14x = –8 | – 7
14x = –15 | : 14

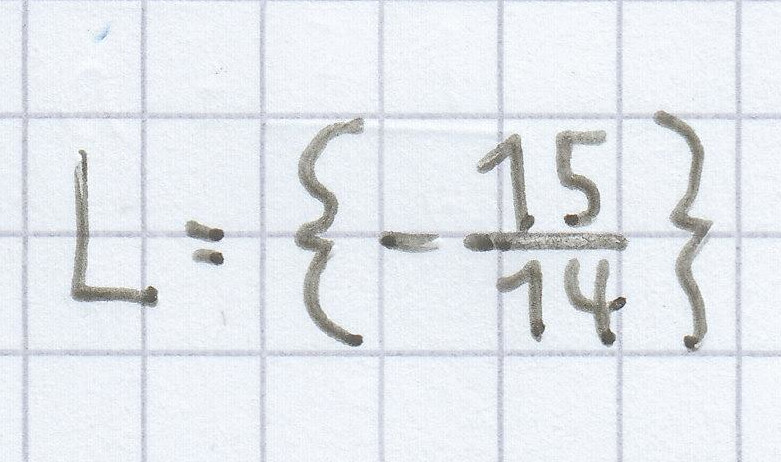
b)
2,1y + 19,4 – 2,8y = 4,7y – 1,1 + 0,7y
–0,7y + 19,4 = 5,4y – 1,1 | + 0,7y
19,4 = 6,1y – 1,1 | + 1,1
20,5 = 6,1y | : 6,1
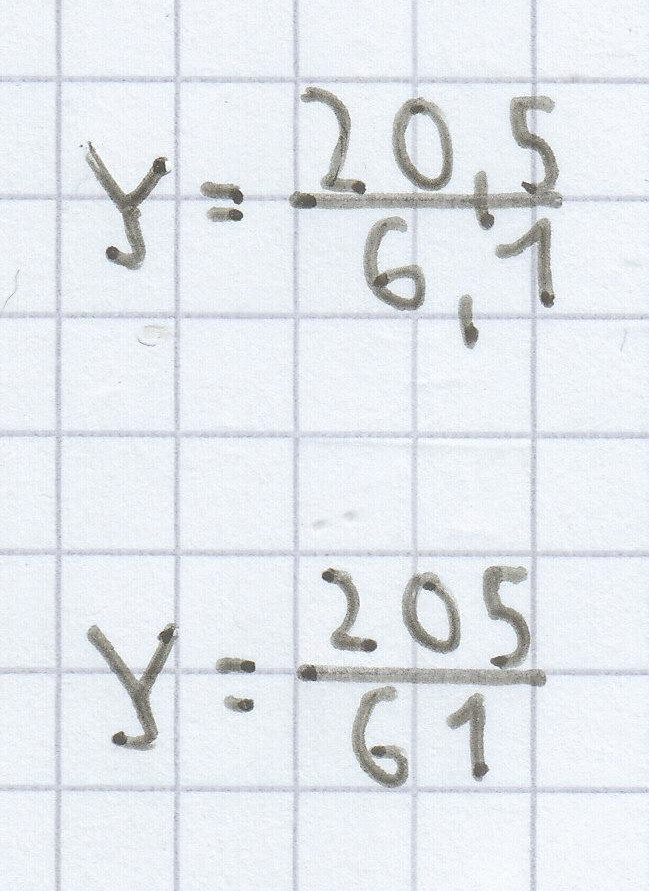
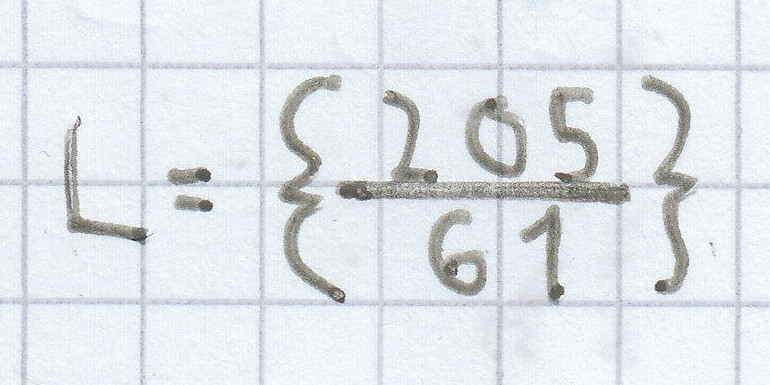
c)
16a – 0,89 = –48a + 0,31 + 56a
16a – 0,89 = 8a + 0,31 | – 8a
8a – 0,89 = 0,31 | + 0,89
8a = 1,2 | : 8
a = 0,15
L = {0,15}
d)
15 – 0,2s + 4 = –1,2s – 21 + 3s
19 – 0,2s = 1,8s – 21 | + 0,2s
19 = 2s – 21 | + 21
40 = 2s | : 2
s = 20
L = {20}