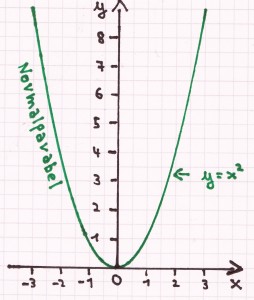
Der bekannteste Graph einer quadratischen Funktion ist die sogenannte Normalparabel. Da es hierfür in Mathe extra eine Schablone gibt, kennt man die Normalparabel normalerweise sehr gut – und deren möglichen Verläufe im Koordinatensystem. Hierfür muss man sich zuvor nur die quadratischen Funktionen genau anschauen. Dann weiß man auch, wo man die Normalparabel im Koordinatensystem einzeichnen muss. Man orientiert sich hierbei an der Funktion y = x². Das stellt die nach oben geöffnete Normalparabel, vom Koordinatenursprung ausgehend, dar. Heißt die Funktion jedoch y = x² + 4, so muss man die Funktion um vier Längeneinheiten nach oben verschieben (entlang der y-Achse). Bei der Funktion y = (x – 4)² um vier Längeneinheiten nach rechts (entlang der x-Achse). Bei der Funktion y = (x – 4)² + 4 um vier Längeneinheiten nach rechts und vier Längeneinheiten nach oben.
Aufgaben zum Mathe-Stoffgebiet Quadratische Funktionen.
1. Mathematik-Nachhilfe-Aufgabe: Mithilfe der Normalparabelschablone soll die Normalparabel verschoben werden.
a) Um 5 Längeneinheiten nach oben.
b) Um 5 Längeneinheiten nach unten.
Gib den Funktionsterm der Funktion an.
Wie sind die Koordinaten des Scheitelpunktes?
2. Mathe-Nachhilfe-Aufgabe: Die Normalparabel soll entlang der y-Achse verschoben werden. Hierbei soll der Punkt P auf der neuen Funktion liegen. Bei der neuen Funktion soll jeweils der Funktionsterm und der Scheitelpunkt angegeben werden.
a) P (0 | –1,6)
b) P (1 | 3,2)
c) P (–1 | 6)
d) P (3 | –4)
e) P (–3 | –6)
3. Mathematik-Nachhilfe-Aufgabe: Es soll der Graph der Funktion f gezeichnet werden. Der Scheitelpunkt soll bestimmt werden, ebenso die Gleichung der Symmetrieachse.
a) f(x) = (x – 3)²
b) f(x) = (x + 1)²
4. Mathe-Nachhilfe-Aufgabe: Die Normalparabel ist um 3 Einheiten nach rechts und 2,6 Einheiten nach unten verschoben worden. Liegen folgende Punkte auf der verschobenen Normalparabel?
a) P1 (1 | 5,4)
b) P2 (4 | 8,6)
c) P3 (6 | 6,4)
d) P4 (–2 | 22,4)
e) P5 (–4 | 52,6)
f) P6 (0 | –2,6)

Lösungen zum Mathematik-Stoffgebiet Quadratische Funktionen
1. Mathe-Nachhilfe-Aufgabe: Die Normalparabel soll mittels Schablone verschoben werden.
a) Um 5 Längeneinheiten nach oben.
b) Um 5 Längeneinheiten nach unten.
Wie lautet der Funktionsterm der Funktion?
Welche Koordinaten hat der Scheitelpunkt?
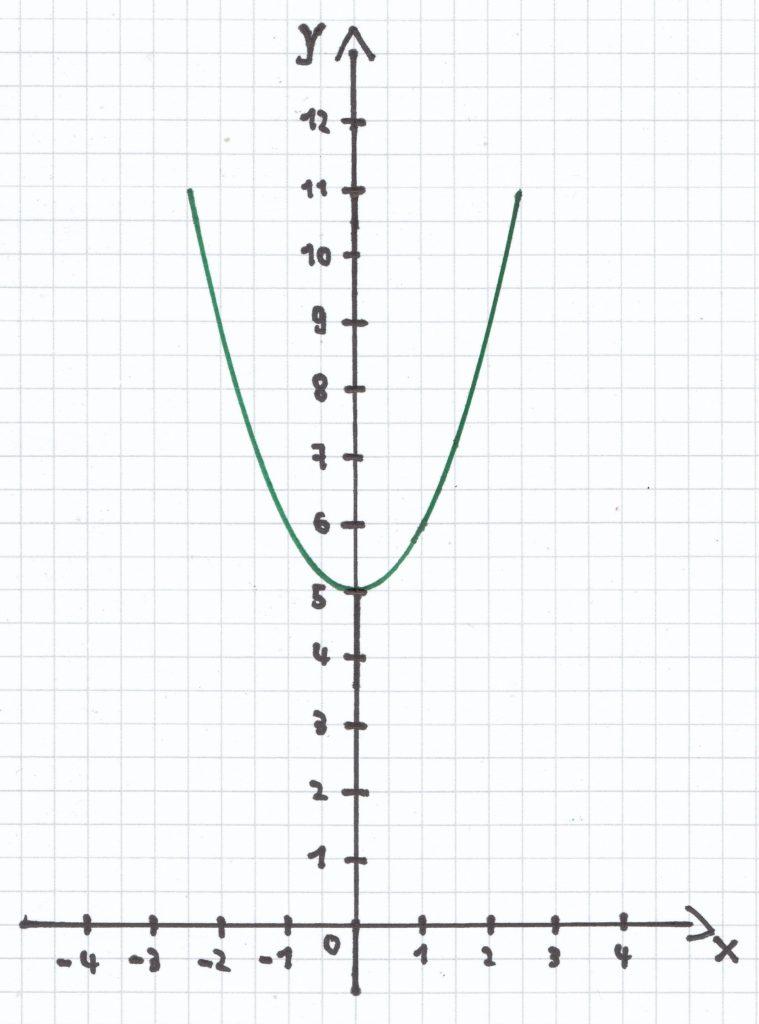
Der Funktionsterm der Funktion ist: x² + 5.
Die Koordinaten des Scheitelpunktes sind: S (0 | 5).
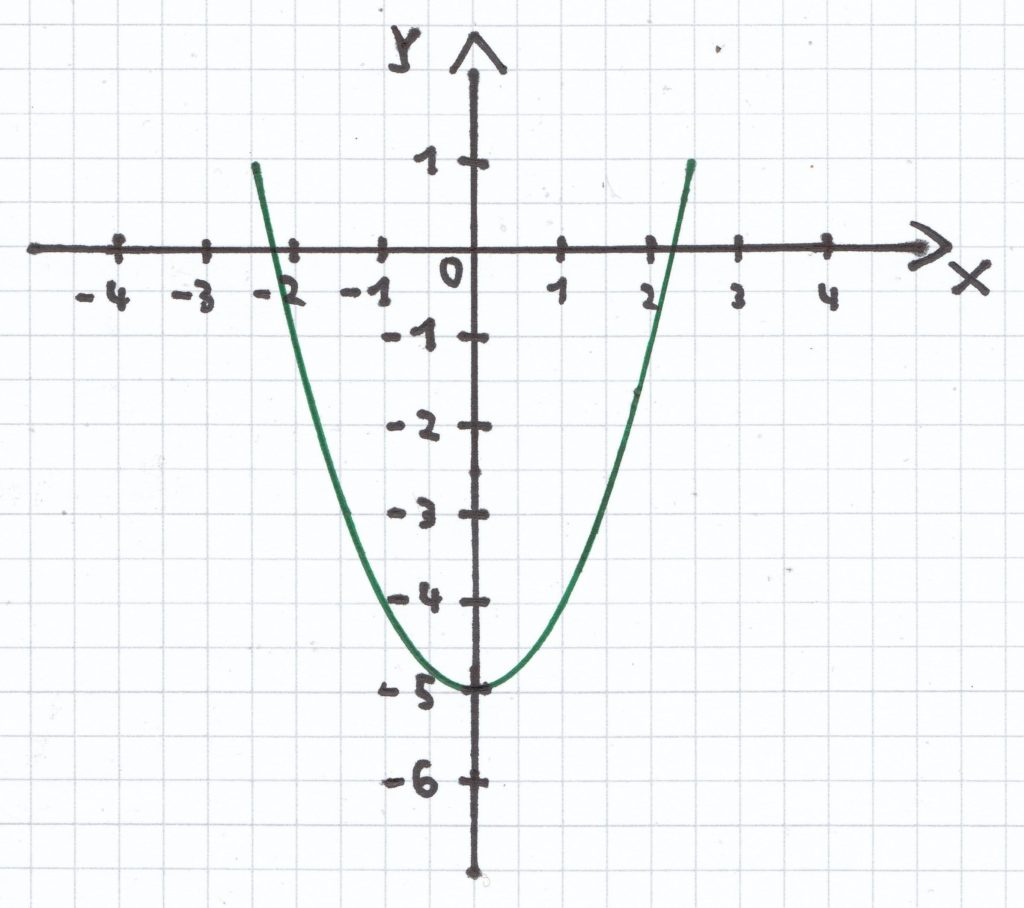
Der Funktionsterm der Funktion lautet: x² – 5.
Der Scheitelpunkt der Funktion ist: S (0 | –5).
2. Mathematik-Nachhilfe-Aufgabe: Die Normalparabl wird entlang der y-Achse verschoben. Der Punkt P soll auf der neuen Funktion liegen. Gib ebenso den Funktionsterm und Scheitelpunkt an.
Die neue Funktion kann man allgemein so wiedergegeben: f(x) = x² + c.
a) P (0 | –1,6)
–1,6 = (0)² + c
c = –1,6
Der Funktionsterm lautet: x² –1,6.
Der Scheitelpunkt ist: S (0 | –1,6).
b) P (1 | 3,2)
3,2 = (1)² + c
3,2 = 1 + c | – 1
c = 2,2
Der Funktionsterm lautet hier: x² + 2,2.
Der Scheitelpunkt ist: S (0 | 2,2).
c) P (–1 | 6)
6 = (–1)² + c
6 = 1 + c | – 1
c = 5
Der Funktionsterm ist: x² + 5.
Der Scheitelpunkt ist: S (0 | 5).
d) P (3 | –4)
–4 = (3)² + c
–4 = 9 + c | – 9
c = –13
Der Funktionsterm lautet hier: x² – 13.
Der Scheitelpunkt ist: S (0 | –13).
e) P (–3 | –6)
–6 = (–3)² + c
–6 = 9 + c | – 9
c = –15
Der Funktionsterm ist: x² – 15.
Der Scheitelpunkt ist: S (0 | –15).
3. Mathe-Nachhilfe-Aufgabe: Zeichne den Graph der Funktion f. Bestimme den Scheitelpunkt der Funktion sowie die Gleichung der Symmetrieachse.
Beide Funktionen sind jeweils entlang der x-Achse verschobene Normalparabeln. Man kann das anhand der Funktionsgleichung sofort sehen.
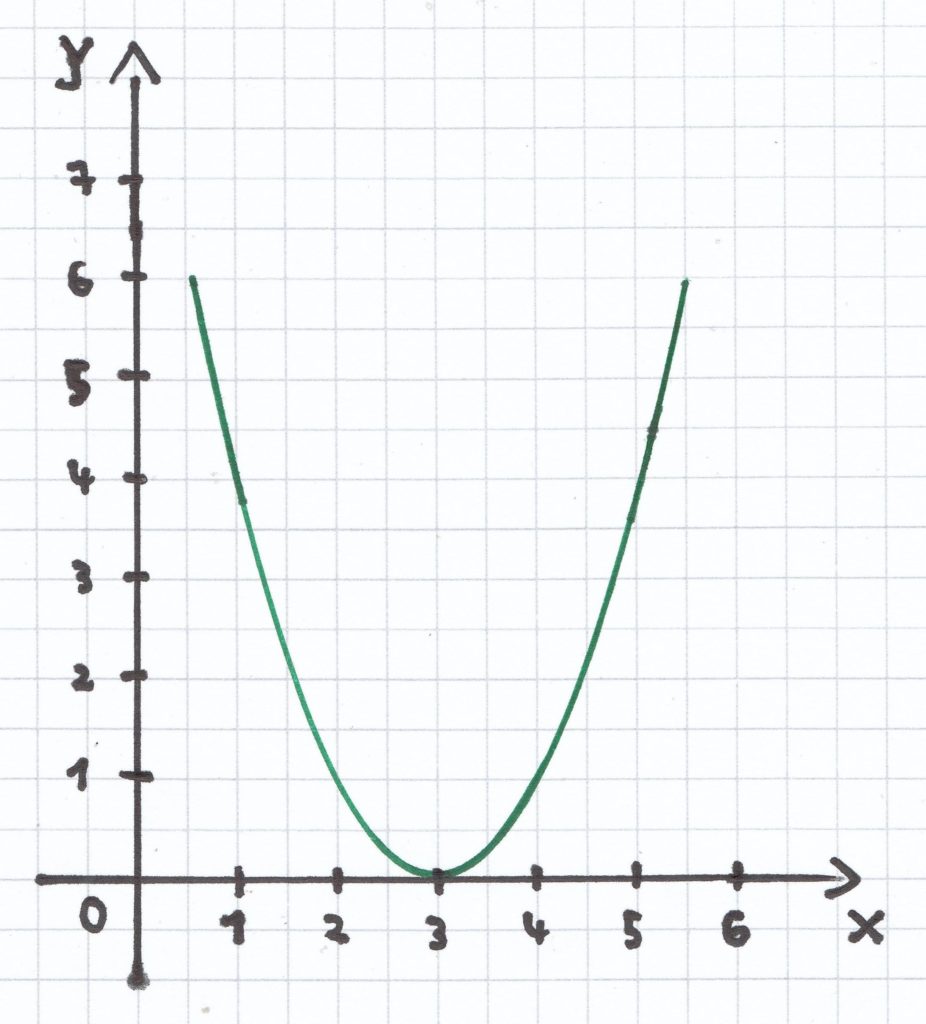
Der Scheitelpunkt der Funktion ist: S (3 | 0).
Die Symmetrieachse ist: x = 3.
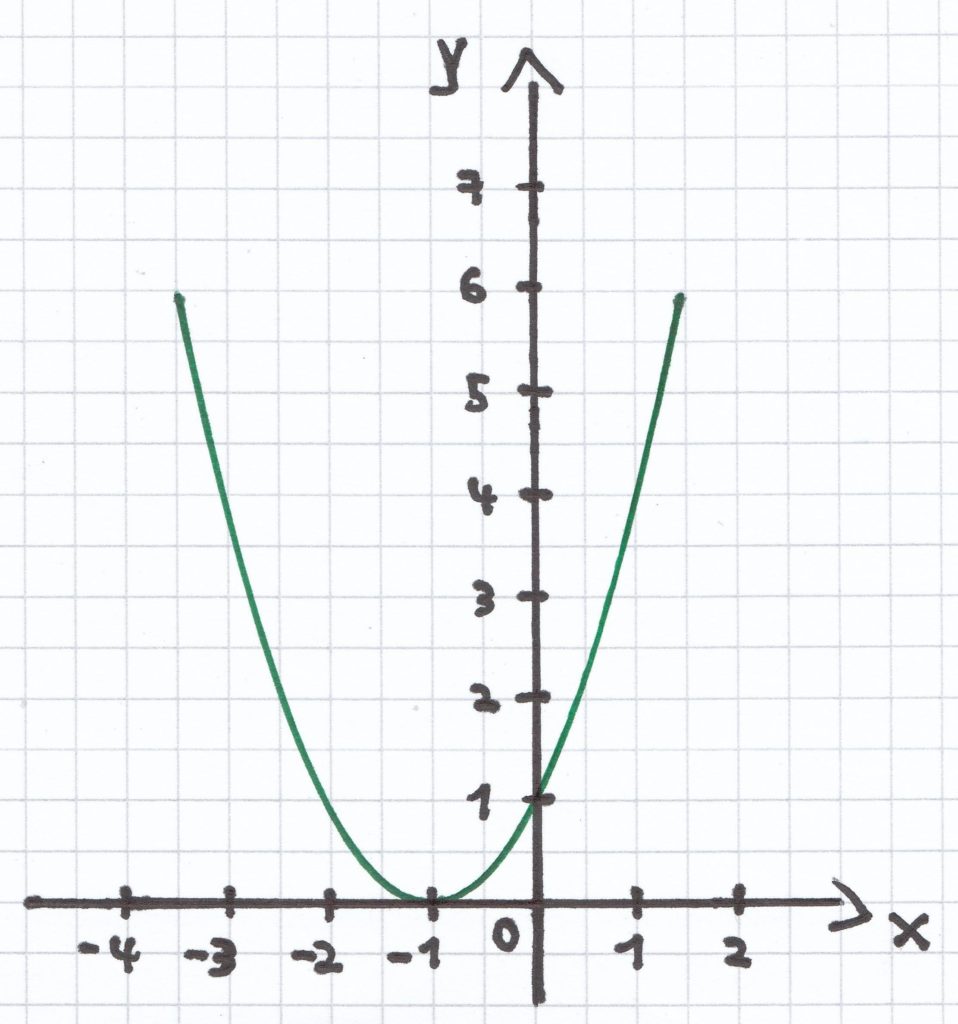
Der Scheitelpunkt der Funkton ist: S (–1 | 0).
Die Gleichung der Symmetrieachse ist: x = –1.
4. Mathematik-Nachhilfe-Aufgagbe: Verschiebe die Normalparabel um 3 Einheiten nach rechts und 2, 6 Einheiten nach unten. Ermittle, ob auf der neuen Funktion die folgenden Punkte liegen.
Bevor man hier eine sogenannte Punktprobe machen kann, muss man die Funktionsgleichung der neuen Funktion aufstellen. Hierbei ist es wichtig, dass man die Verschiebungen der Normalparabel im Koordinatensystem in die korrekte algebraische Form umwandelt.
3 Einheiten nach rechts ist: (x – 3)²
2,6 Einheiten nach unten ist: –2,6
Hieraus ergibt sich diese Funktionsgleichung: f(x) = (x – 3)² – 2,6.
a) P1 (1 | 5,4)
5,4 = (1 – 3)² – 2,6
5,4 = (–2)² – 2,6
5,4 = 4 – 2,6
5,4 = 1,4
Der Punkt P1 liegt nicht auf der Funktion.
b) P2 (4 | 8,6)
8,6 = (4 – 3)² – 2,6
8,6 = (1)² – 2,6
8,6 = 1 – 2,6
8,6 = –1,6
Der Punkt P2 liegt nicht auf der Funktion.
c) P3 (6 | 6,4)
6,4 = (6 – 3)² – 2,6
6,4 = (3)² – 2,6
6,4 = 9 – 2,6
6,4 = 6,4
Der Punkt P3 liegt auf der Funktion.
d) P4 (–2 | 22,4)
22,4 = (–2 – 3)² – 2,6
22,4 = (–5)² – 2,6
22,4 = 25 – 2,6
22,4 = 22,4
Der Punkt P4 liegt auf der Funktion.
e) P5 (–4 | 52,6)
52,6 = (–4 – 3)² – 2,6
52,6 = (–7)² – 2,6
52,6 = 49 – 2,6
52,6 = 46,4
Der Punkt P5 liegt nicht auf der Funktion.
f) P6 (0 | –2,6)
–2,6 = (0 – 3)² – 2,6
–2,6 = (–3)² – 2,6
–2,6 = 9 – 2,6
–2,6 = 6,4
Der Punkt P6 liegt nicht auf der Funktion.