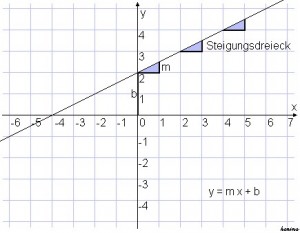
Eine Funktion kann man in Mathe immer grafisch darstellen, und zwar in einem Koordinatensystem. Diesen optischen Verlauf einer Funktion nennt man den Graph der Funktion. Einfache Funktionen wie lineare Funktionen und quadratische Funktionen kann man hierbei recht einfach in ein Koordinatensystem einzeichnen. Bei höheren Funktionen wie ganzrationale Funktionen 3. oder 4. Grades oder gebrochenrationalen Funktionen ist das schon um einiges schwieriger. Umso wichtiger ist es daher, dass bei solchen Funktionen vorher eine genaue Wertetabelle aufgestellt wird, die in einem bestimmten Intervall aufs Beste den Verlauf der Funktion optisch veranschaulicht. Was bei einer Funktion aber alles zu beachten ist, das lernt man in Mathematik schrittweise bzw. von Funktion zu Funktion – und das ab der Mittelstufe.
Aufgaben zum Mathe-Stoffgebiet Funktionen, Teil 2
1. Mathematik-Nachhilfe-Aufgabe: Ermittle verschiedene Werte einer Funktion mit vorgegebener Funktionsvorschrift. Was für einen Wert hat die jeweilige Funktion an der Stelle 0; 0,5; 1; 1,4; 4; –4; –1,4; –1; –0,5? An welchen Stellen der Funktion ist der Funktionswert 4 [2,25; 0,64; 1,96]
a) x[latexpage] ${\mapsto}$ 100x²
b) a[latexpage] ${\mapsto}$ a²
c) s[latexpage] ${\mapsto}$ (s – 1)²
d) t[latexpage] ${\mapsto}$ 0,25t²
2. Mathe-Nachhilfe-Aufgabe: Löse die Gleichung zuerst nach y hin auf. Prüfe darauf durch eindeutiges Einsetzen von Zahlen für x, ob ein eindeutiger y-Wert definitiv vorliegt.
a) 2 – x = –y + 2
b) y² = x
c) (x + y)² = 4
d) x + 3 = y + 2
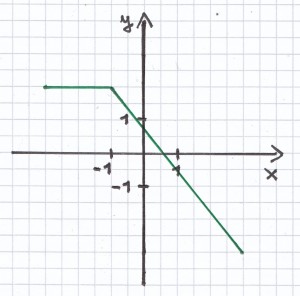
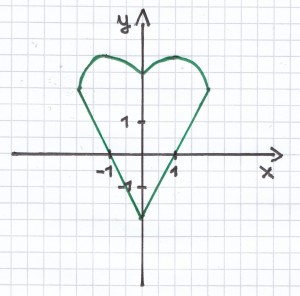
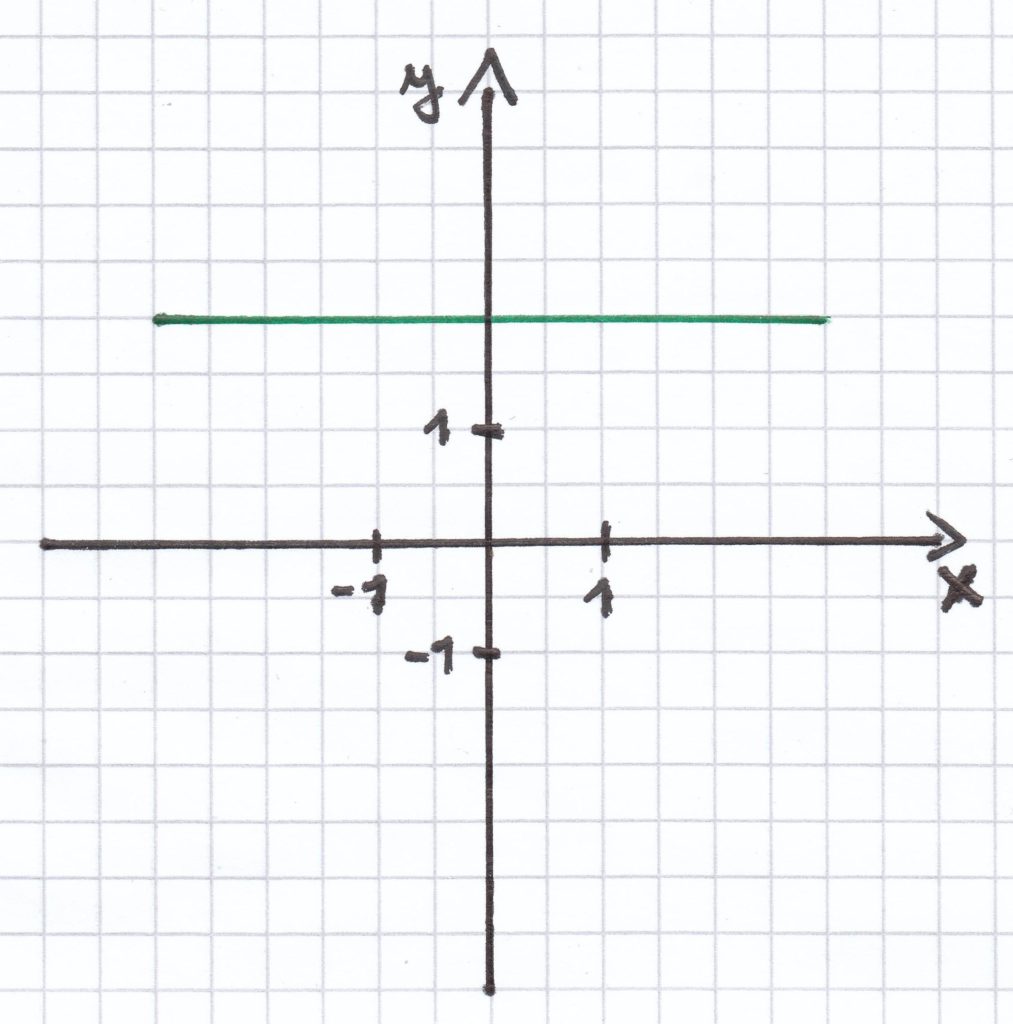
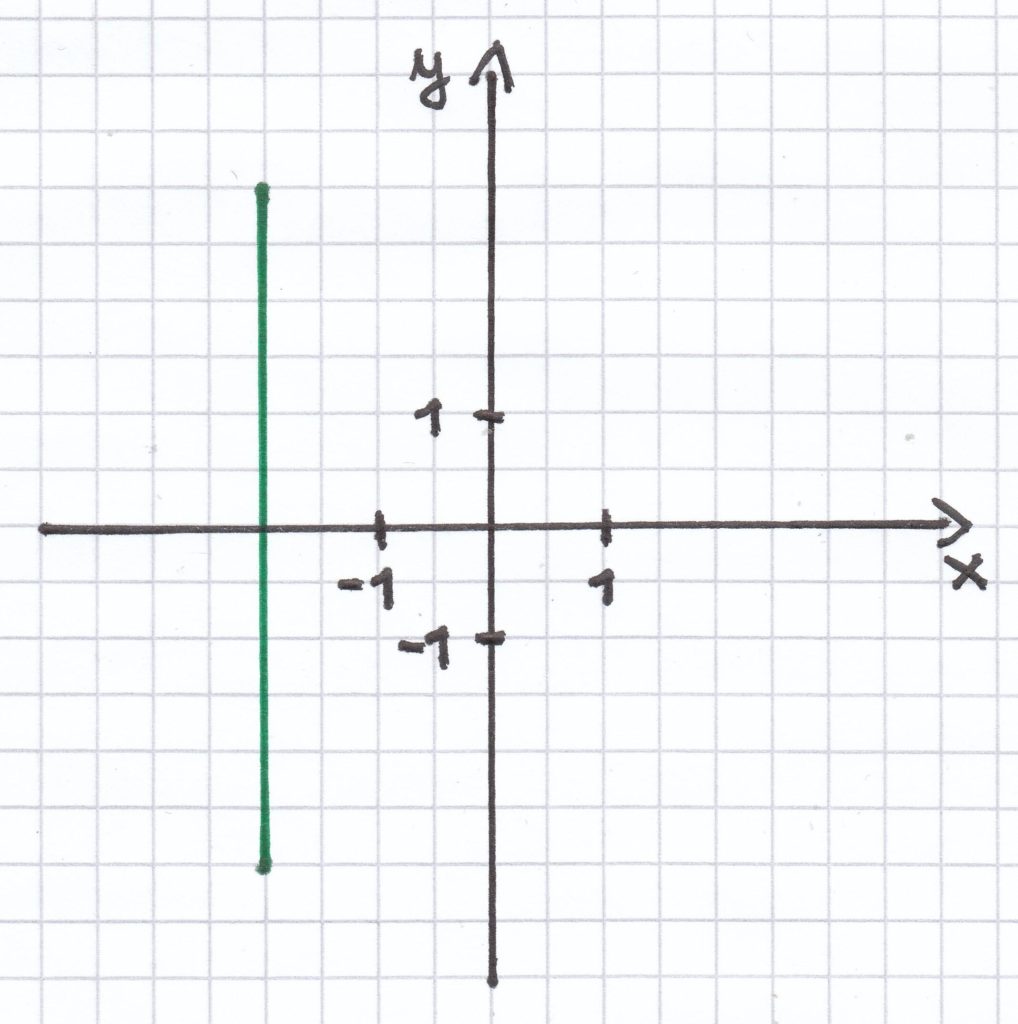
3. Mathematik-Nachhilfe-Aufgabe: Liegt bei dem Graph eine Funktion vor? Begründe jeweils die Antwort.
4. Mathe-Nachhilfe-Aufgabe: Zeichne den Graphen. Mach vorher eine Wertetabelle.
a) x[latexpage] ${\mapsto}$ 0,6 ∙ x
b) x[latexpage] ${\mapsto}$ (x + 2)²
c) x[latexpage] ${\mapsto}$ 6 – ${\frac{\mathrm x}{2}}$
d) x[latexpage] ${\mapsto}$ x ∙ (6 + x)
Lösungen zum Mathe-Stoffgebiet Funktionen
1. Mathe-Nachhilfe-Aufgabe: Bestimme die unterschiedlichen Werte einer Funktion mit vorgegebener Funktionsvorschrift. Wie ist der Wert der Funktion an des Stelle 0; 0,5; 1; 1,4; 4; –4; –1,4; –1; –0,5? Wo hat die Funktion den Funktionswert 4 [2,25; 0,64; 1,96]?
a) x[latexpage] ${\mapsto}$ 100x²
für x = 0 gilt: 100 · (0)² = 100 · 0 = 0
Mathematik-Nachhilfe-Hinweis: Zur Berechnung von Werten einer Funktion siehe auch unter dem Reiter Terme 3. Wertberechnung bei einem Term an.
für x = 0,5 gilt: 100 · (0,5)² = 100 · 0,25 = 25
für x = 1 gilt: 100 · (1)² = 100 · 1 = 100
für x = 1,4 gilt: 100 · (1,4)² = 100 · 1,96 = 196
für x = 4 gilt: 100 · (4)² = 100 · 16 = 1600
für x = –4 gilt: 100 · (–4)² = 100 · 16 = 1600
für x = –1,4 gilt: 100 · (–1,4)² = 100 · 1,96 = 196
für x = –1 gilt: 100 · (–1)² = 100 · 1 = 100
für x = –0,5 gilt: 100 · (–0,5)² = 100 · 0,25 = 25
Der Funktionswert entspricht dem y-Wert einer Funktion. Bei vorgegebenem Funktionswert ergibt sich hier daher automatisch eine Gleichung, die man nach der Variablen hin auflösen muss. Hierdurch ergibt sich die Stelle der Funktion für den gegebenen Funktionswert.
für y = 4 gilt: 100x² = 4 | : 100
x² = 0,04 | √
x = ± 0,2
für y = 2,25 gilt: 100x² = 2,25 | : 100
x² = 0,0225 | √
x = ± 0,15
für y = 0,64 gilt: 100x² = 0,64 | : 100
x² = 0,0064 | √
x = ± 0,08
für y = 1,96 gilt: 100x² = 1,96 | : 100
x² = 0,0196 | √
x = ± 0,14
b) a[latexpage] ${\mapsto}$ a²
für a = 0 gilt: (0)² = 0
für a = 0,5 gilt: (0,5)² = 0,25
für a = 1 gilt: (1)² = 1
für a = 1,4 gilt: (1,4)² = 1,96
für a = 4 gilt: (4)² = 16
für a = –4 gilt: (–4)² = 16
für a = –1,4 gilt: (–1,4)² = 1,96
für a = –1 gilt: (–1)² = 1
für a = –0,5 gilt: (–0,5)² = 0,25
für b = 4 gilt: a² = 4 | √
a = ± 2
für b = 2,25 gilt: a² = 2,25 | √
a = ± 1,5
für b = 0,64 gilt: a² = 0,64 | √
a ± 0,8
für b = 1,96 gilt: a² = 1,96 | √
a = ± 1,4
c) s[latexpage] ${\mapsto}$ (s – 1)²
für s = 0 gilt: (0 – 1)² = (1)² = 1
für s = 0,5 gilt: (0,5 – 1)² = (–0,5)² = 0,25
für s = 1 gilt: (1 – 1)² = (0)² = 0
für s = 1,4 gilt: (1,4 – 1)² = (0,4)² = 0,16
für s = 4 gilt: (4 – 1)² = (3)² = 9
für s = –4 gilt: (–4 – 1)² = (–5)² = 25
für s = –1,4 gilt: (–1,4 – 1)² = (–2,4)² = 5,76
für s = –1 gilt: (–1 – 1)² = (–2)² = 4
für s = –0,5 gilt: (–0,5 – 1)² = (–1,5)² = 2,25
für t = 4 gilt: (s – 1)² = 4 | √
s – 1 = ± 2 | + 1
s = ± 2 + 1
s$_1$ = 2 + 1 = 3
s$_2$ = –2 + 1 = –1
für t = 2,25 gilt: (s – 1)² = 2,25 | √
s – 1 = ± 1,5 | + 1
s = ± 1,5 + 1
s$_1$ = 1,5 + 1 = 2,5
s$_2$ = –1,5 + 1 = –0,5
für t = 0,64 gilt: (s – 1)² = 0,64 | √
s – 1 = ± 0,8 | + 1
s = ± 0,8 + 1
s$_1$ = 0,8 + 1 = 1,8
s$_2$ = –0,8 + 1 = 0,2
für t = 1,96 gilt: (s – 1)² = 1,96 | √
s – 1 = ± 1,4 | + 1
s = ± 1,4 + 1
s$_1$ = 1,4 + 1 = 2,4
s$_2$ = –1,4 + 1 = –0,4
d) t[latexpage] ${\mapsto}$ 0,25t²
für t = 0 gilt: 0,25 · (0)² = 0,25 · 0 = 0
für t = 0,5 gilt: 0,25 · (0,5)² = 0,25 · 0,25 = 0,0625
für t = 1 gilt: 0,25 · (1)² = 0,25 · 1 = 0,25
für t = 1,4 gilt: 0,25 · (1,4)² = 0,25 · 1,96 = 0,49
für t = 4 gilt: 0,25 · (4)² = 0,25 · 16 = 4
für t = –4 gilt: 0,25 · (–4)² = 0,25 · 16 = 4
für t = –1,4 gilt: 0,25 · (–1,4)² = 0,25 · 1,96 = 0,49
für t = –1 gilt: 0,25 · (–1)² = 0,25 · 1 = 0,25
für t = –0,5 gilt: 0,25 · (–0,5)² = 0,25 · 0,25 = 0,0625
für u = 4 gilt: 0,25t² = 4 | : 0,25
t² = 16 | √
t = ± 4
für u = 2,25 gilt: 0,25t² = 2,25 | : 0,25
t² = 9 | √
t = ± 3
für u = 0,64 gilt: 0,25t² = 0,64 | : 0,25
t² = 2,56 | √
t = ± 1,6
für u = 1,96 gilt: 0,25t² = 1,96 | : 0,25
t² = 7,84 | √
t = ± 2,8
2. Mathematik-Nachhilfe-Aufgabe: Forme die Gleichung nach y hin um. Untersuche durch eindeutiges Einsetzen, ob definitiv ein eindeutiger y-Wert vorliegt.
a) 2 – x = –y + 2 | – 2
–x = –y | · (–1)
x = y
für x = 1 gilt: y = 1
für x = 0 gilt: y = 0
für x = –1 gilt: y = –1
Es liegt immer eine eindeutige Zuordnung vor: Ein x-Wert wird ein y-Wert zugeordnet. Daher liegt hier auch eine Funktion vor.
b) y² = x | √
y = ±$\sqrt{\mathrm x}}$
Hier ergeben sich von Anfang an keine eindeutigen x-Werte und daher auch keine eindeutigen y-Werte. Hier liegt demzufolge auch keine Funktion vor.
c) (x + y)² = 4 | √
x + y = ± 2 | – x
y = ± 2 – x
Hier ergeben sich auch keine eindeutigen x-Werte und somit keine eindeutigen y-Werte. Daher liegt hier ebenso keine Funktion vor.
d) x + 3 = y + 2 | – 2
x + 1 = y
für x = 1 gilt: y = 1 + 1; y = 2
für x = 0 gilt: y = 0 + 1; y = 1
für x = –1 gilt: y = –1 + 1; y = 0
3. Mathe-Nachhilfe-Aufgabe: Handelt es sich bei dem Graphen um eine Funktion. Begründe dies.

Hier liegt eine Funktion vor. Es handelt sich hier um eine abschnittweise definierte lineare Funktion. Jeder x-Wert hat hier eine eindeutige y-Wert-Zuordnung.

Hier liegt keine Funktion vor. Es gibt viele x-Werte die mehrfache y-Werte vorweisen.

Hier handelt es sich um eine lineare Funktion. Jeder x-Wert weist einen eindeutigen y-Wert auf.

Hier liegt keine Funktion vor. Es gibt nur einen x-Wert, der unendliche viele y-Werte vorweist.
4. Mathe-Nachhilfe-Aufgabe: Zeichne den Graphen der Funktion in ein Koordinatensystem. Mache vorher eine Wertetabelle.
a) x[latexpage] ${\mapsto}$ 0,6 ∙ x
Wertetabelle: Wertetabelle Aufgabe a)
Graph der Funktion: Graph der Funktion, Aufgabe a)
b) x[latexpage] ${\mapsto}$ (x + 2)²
Wertetabelle: Wertetabelle Aufgabe b)
Graph der Funktion: Graph der Funktion, Aufgabe b)
c) x[latexpage] ${\mapsto}$ 6 – ${\frac{\mathrm x}{2}}$
Wertetabelle: Wertetabelle Aufgabe c)
Graph der Funktion: Graph der Funktion, Aufgabe c)
d) x[latexpage] ${\mapsto}$ x ∙ (6 + x)