
Als Schülerin und Schüler lernt man in Mathe als erste Funktionen lineare Funktionen kennen. „Das sind Geraden“, sagt ein emsiger Eleve, als er von seinen Eltern gefragt wird, was das sind. „Den Graph einer linearen Funktion nennt man Gerade“, antwortet der Lehrer bei einem Elternabend auf die gleiche Frage einer Elternhälfte. Der Lehrer muss das auch haargenau so sagen, denn die Darstellung einer linearen Funktion in einem Koordinatensystem ergibt eine Gerade. „Lineare Funktionen kann man aber nicht nur im Koordinatensystem darstellen“, ergänzt er weiter. „Lineare Funktionen weisen auch einen Funktionsterm auf, anhand dem man verschiedene Berechnungen machen kann – die auch wiederum an deren Graph ablesbar sind.“ „Aha“, hört man dann die Eltern sagen.
Aufgaben zum Mathe-Stoffgebiet Lineare Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Untersuche die Funktionsgleichungen hinsichtlich ihrer Schnittpunkte mit der x- und y-Achse. Liegt der Punkt P (1 | 2) auf der Funktion? Löse die Aufgabe rein rechnerisch.
a) y = 5x – 3
b) y = –1,5x + 1
c) y = [latexpage] –${\frac{1}{2}}$x + 2
d) y = ${\frac{1}{2}}$x + 1,5
2. Mathe-Nachhilfe-Aufgabe: Zeichne die Graphen der linearen Funktionen in ein Koordinatensystem. Wähle hierzu den Ordinatenabschnitt und die Steigung zum Einzeichnen der Funktion.
a) f(x) = 3x + 1
b) f(x) = 0,5x – 2
c) f(x) = –2x – 4
3. Mathematik-Nachhilfe-Aufgabe: In alle gegebenen Funktionen sollen nacheinander folgende Terme eingesetzt werden und gegebenenfalls danach auch die Funktion vereinfacht werden: –r rür x; 3r für x; 2r + 2 für x; 3 – 2r.
a) f(x) = 5x
b) f(x) = 1,5x – 4
c) f(x) = 4x – 5
d) f(x) = –2x + 3
4. Mathe-Nachhilfe-Aufgabe: Es ist eine 32 cm lange Kerze gegeben. Pro Stunde nimmt deren Länge um 1,5 cm ab, wenn diese brennt.
a) Ermittle für die Kerzenlänge und die Brenndauer eine Zuordnungsvorschrift und eine Funktionsgleichung.
b) Zeichne den Graphen dieser Funktion.
c) Berechne die Höhe der Kerze nach 3 [7; 10,5; 15 und 20] Stunden
d) Ermitte, wann die Kerze die Höhe 1,8 cm hat.
e) Bestimme die Zeitdauer, wie lange die Kerze brennt.
Lösungen zum Mathematik-Stoffgebiet Lineare Funktionen
1. Mathe-Nachhilfe-Aufgabe: Ermittle bei den Funktionsgleichungen deren Schnittpunkte mit der x- und y-Achse. Zu welchen Funktionen gehört der der Punkt P (1 | 2) zum Graphen der Funktion? Löse die Aufgabe nur mittels Rechnung.
a) y = 5x – 3
Um den Schnittpunkt mit der x-Achse zu ermitteln, muss man die Funktionsgleichung gleich null setzen (y = 0) und nach der Variablen hin auflösen.
0 = 5x – 3 | + 3
3 = 5x | : 5
x = ${\frac{3}{5}}$
Der Schnittpunkt mit der x-Achse ist: P (${\frac{3}{5}}$ | 0).
Um den Schnittpunkt mit der y-Achse zu ermitteln, muss man x gleich null setzen (x = 0). Die Gleichung ist dann nach der Variablen y bereits aufgelöst.
y = 5 · 0 – 3
y = –3
Die Funktion hat folgenden Schnittpunkt mit der y-Achse: P (0 | –3).
Ob der Punkt P (1 | 2) auf dem Graphen der linearen Funktion liegt, ermittelt man mittels der Punktprobe. Man setzt einfach den Punkt in die Funktion ein. Liegt der Punkt auf der Funktion, dann muss die Gleichung eine wahre Aussage ergeben.
2 = 5 · (1) – 3
2 = 5 – 3
2 = 2
Hier liefert die Punktprobe eine wahre Aussage. Der Punkt P (1 | 2) liegt auf der Funktion.
b) y = –1,5x + 1
Schnittpunkt mit der x-Achse:
0 = –1,5x + 1 | + 1,5x
1,5x = 1 | : 1,5
x = ${\frac{1}{1,5}}$
x = ${\frac{10}{15}}$
x = ${\frac{2}{3}}$
Der Schnittpunkt mit der x-Achse ist: P (${\frac{2}{3}}$ | 0).
Schnittpunkt mit der y-Achse:
y = –1,5 · 0 + 1
y = 1
Der Schnittpunkt mit der y-Achse ist: P (0 | 1).
Punktprobe zu dem Punkt P (1 | 2):
2 = –1,5 · 1 + 1
2 = –1,5 + 1
2 = –0,5
Die Gleichung liefert keine wahre Aussage. Der Punkt P (1 | 2) gehört daher nicht zu der Funktion.
c) y = –${\frac{1}{2}}$x + 2
Schnittpunkt mit der x-Achse:
0 = –${\frac{1}{2}}$x + 2 | + ${\frac{1}{2}}$x
${\frac{1}{2}}$x = 2 | · 2
x = 4
Der Schnittpunkt mit der x-Achse ist: P (4 | 0).
Schnittpunkt mit der y-Achse:
y = –${\frac{1}{2}}$ · 0 + 2
y = 2
Der Schnittpunkt mit der y-Achse ist: P (0 | 2).
Punktprobe:
2 = –${\frac{1}{2}}$ · 1 + 2
2 = –${\frac{1}{2}}$ + 2
2 = 1,5
Der Punkt P (1 | 2) liegt nicht auf der Funktion, da die Punktprobe keine wahre Aussage der Gleichung liefert.
d) y = ${\frac{1}{2}}$x + 1,5
Schnittpunkt mit der x-Achse:
0 = ${\frac{1}{2}}$x + 1,5 | – 1,5
–1,5 = ${\frac{1}{2}}$x | · 2
x = –3
Der Schnittpunkt mit der x-Achse ist: P (–3 | 0).
Schnittpunkt mit der y-Achse:
y = ${\frac{1}{2}}$ · 0 + 1,5
y = 1,5
Der Schnittpunkt mit der y-Achse ist: P (0 | 1,5).
Punktprobe:
2 = ${\frac{1}{2}}$ · 1 + 1,5
2 = ${\frac{1}{2}}$ + 1,5
2 = 2
Die Gleichung liefert eine wahre Aussage. Der Punkt P (1 | 2) liegt auf der Funktion.
2. Mathematik-Nachhilfe-Aufgabe: Es soll der Graph von linearen Funktionen gezeichnet werden. Vom Ordinatenabschnitt ausgehend, soll die Funktion und deren Steigung in ein Koordinatensystem eingezeichnet werden.
Der Ordinatenabschnitt bei einer linearen Funktion ist immer der Term ohne Variable bzw. der y-Wert, wenn x gleich null ist.
Die Steigung bei einer linearen Funktion ist immer die Zahl, die vor der Variablen x steht.
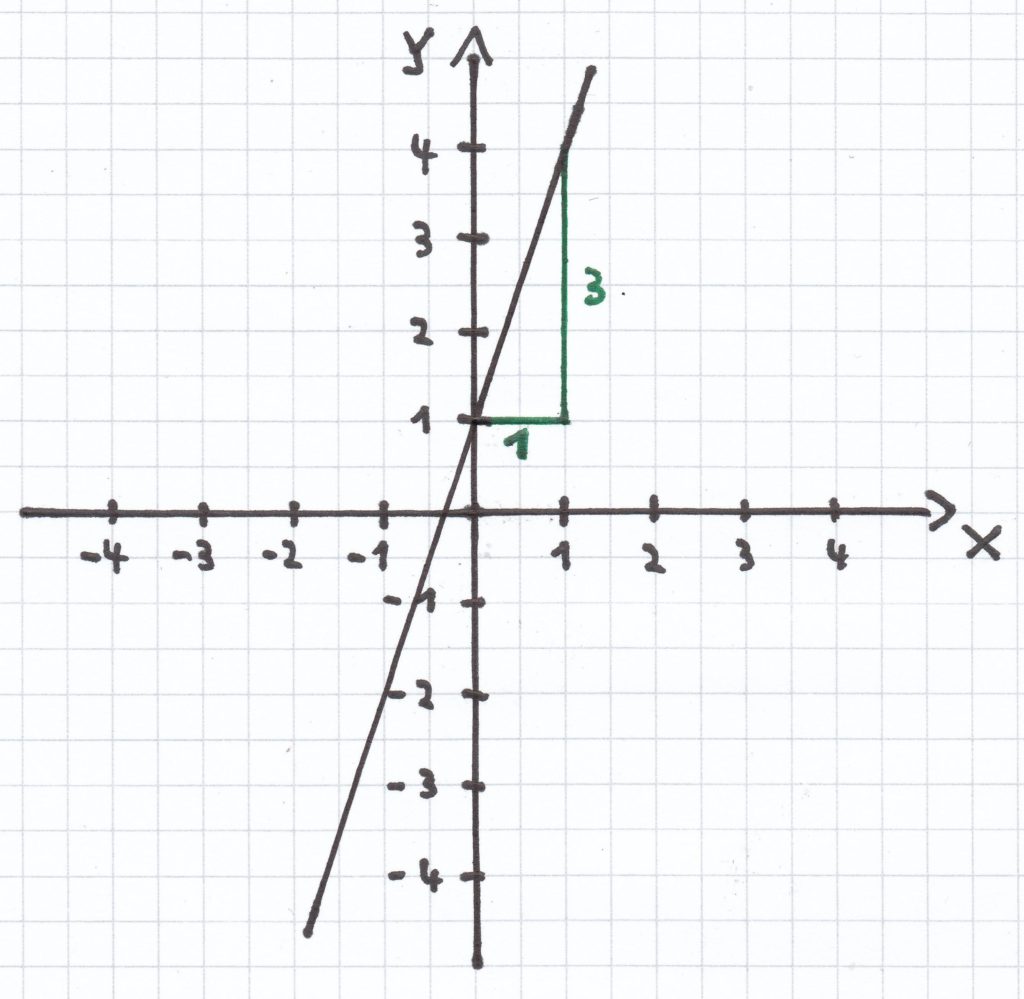
a) f(x) = 3x + 1
Der Ordinatenabschnitt ist hier: y = 1.
Die Steigung der Funktion ist hier: m = 3.
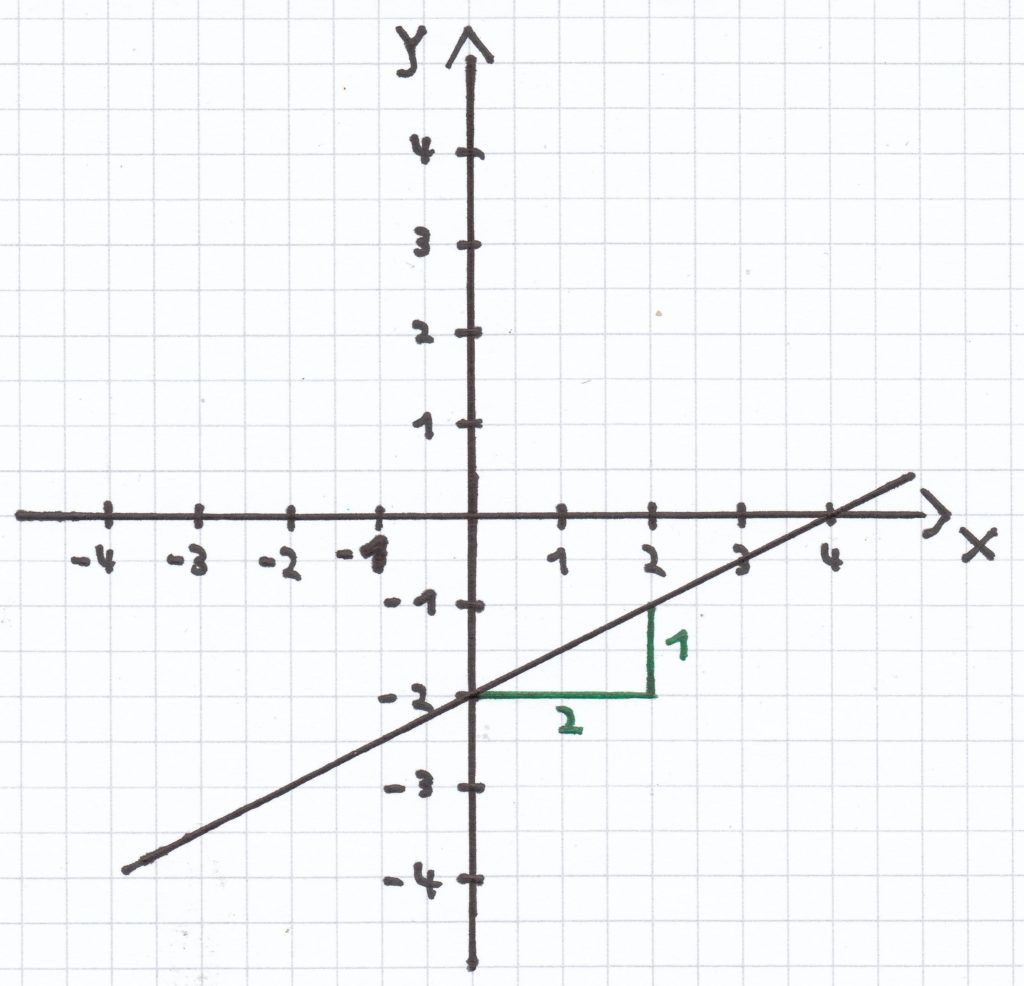
b) f(x) = 0,5x – 2
Der Ordinatenabschnitt ist hier: y = –2.
Die Steigung ist hier: m = 0,5.
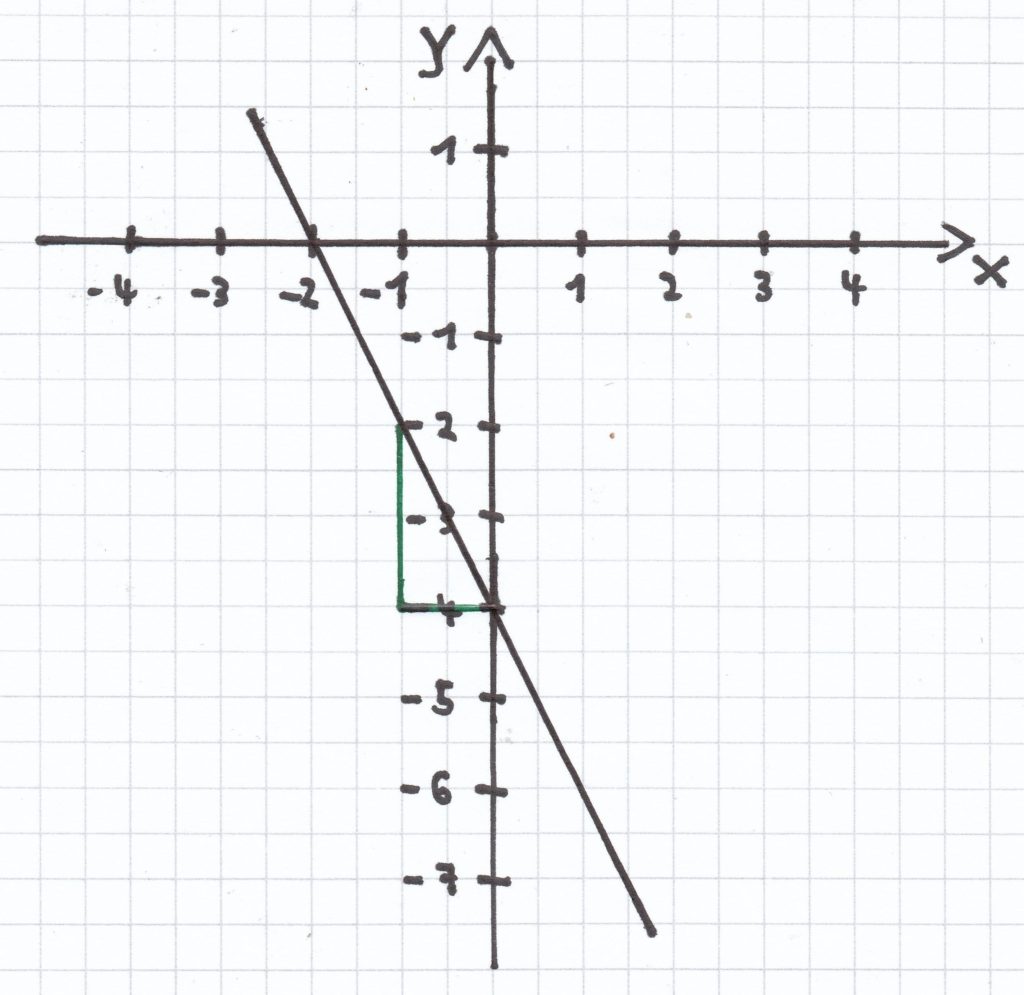
c) f(x) = –2x – 4
Der Ordinatenabschnitt ist: y = –4.
3. Mathe-Nachhilfe-Aufgabe: Setze alle hier gegebenen Terme in die Funktionen ein und vereinfache die Funktionsterme gegebenenfalls: –r rür x; 3r für x; 2r + 2 für x; 3 – 2r.
a) f(x) = 5x
f(–r) = 5(–r)
f(–r) = –5r;
f(3r) = 5(3r)
f(3r) =15r;
f(2r + 2) = 5(2r + 2)
f(2r + 2) =10r + 10;
f(3 – 2r) = 5(3 – 2r)
f(3 – 2r) = 15 – 10r;
f(3 – 2r) = –10r + 15
b) f(x) = 1,5x – 4
f(–r) = 1,5(–r) – 4
f(–r) = –1,5r – 4;
f(3r) = 1,5(3r) – 4
f(3r) = 4,5r – 4;
f(2r + 2) = 1,5(2r + 2) – 4
f(2r + 2) = 3r + 3 – 4;
f(2r + 2) = 3r – 1;
f(3 – 2r) = 1,5(3 – 2r) – 4
f(3 – 2r) = 4,5 – 3r – 4;
f(3 – 2r) = –3r + 0,5
c) f(x) = 4x – 5
f(–r) = 4(–r) – 5
f(–r) = –4r – 5;
f(3r) = 4(3r) – 5
f(3r) =12r – 5;
f(2r + 2) = 4(2r + 2) – 5
f(2r + 2) = 8r + 8 – 5;
f(2r + 2) =8r + 3;
f(3 – 2r) = 4(3 – 2r) – 5
f(3 – 2r) = 12 – 8r – 5;
f(3 – 2r) = –8r + 7
d) f(x) = –2x + 3
f(–r) = –2(–r) + 3
f(–r) = 2r + 3;
f(3r) = –2(3r) + 3
f(3r) = –6r + 3;
f(2r + 2) = –2(2r + 2) + 3
f(2r + 2) = –4r – 4 + 3;
f(2r + 2) = –4r – 1;
f(3 – 2r) = –2(3 – 2r) + 3
f(3 – 2r) = –6 + 4r + 3;
f(3 – 2r) = 4r – 3
4. Mathematik-Nachhilfe-Aufgabe: Eine 32 cm lange Kerze verliert pro Stunden 1,5 cm ihrer Länge, wenn sie brennt.
a) Bestimme für die Kerzenlänge und die Brenndauer eine Zuordnungsvorschrift sowie eine Funktionsgleichung.
Die Zuordnungsvorschrift ist hier Folgende: x[latexpage] ${\mapsto}$ 32 – 1,5x.
Die Kerze hat ja anfangs die Länge 32 cm. Deshalb der Term „32“. Pro Stunde wird die Kerze um 1,5 cm kleiner. Daher der Term „–1,5x“.
Die Funktionsgleichung ist: f(x) = 32 – 1,5x.
b) Zeichne den Graphen der Funktion in ein Koordinatensystem.
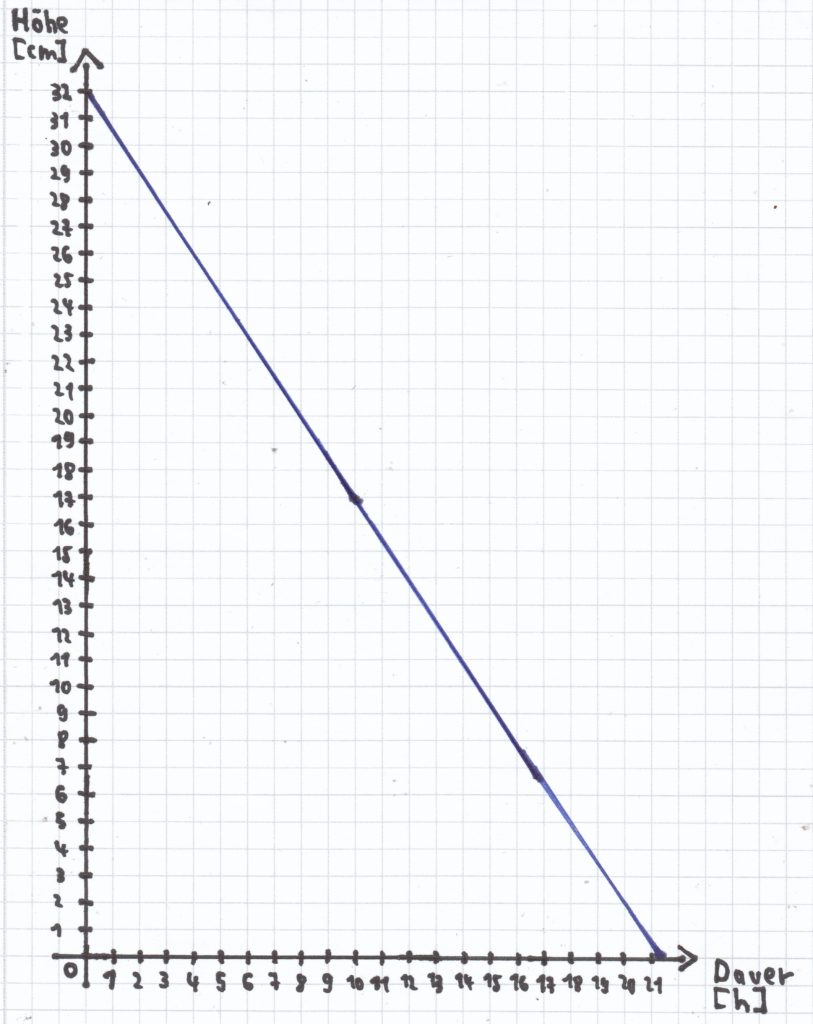
Die Höhe am Anfang der Kerze ist ja 32 cm.
Jetzt kann man zum Beispiel noch die Höhe nach 10 Stunden Brenndauer ausrechnen: y = 32 – 1,5(10); y = 32 – 15; y = 17.
Nun hat man zwei y-Werte und kann hierdurch eine Strecke im Koordinatensystem bis zur x-Achse hin einzeichnen. Die Funktion verläuft nur im 1. Quadranten, da die Kerzenlänge ja nicht negativ werden kann (die y-Werte) und die Höhe der Kerze maximal 32 cm ist.
c) Welche Höhe hat die Kerze nach 3 [7; 10,5; 15 und 20] Stunden?
f(x) = 32 – 1,5x
f(3) = 32 – 1,5(3)
f(3) = 32 – 4,5
f(3) = 27,5
f(7) = 32 – 1,5(7)
f(7) = 32 – 10,5
f(7) = 21,5
f(10,5) = 32 – 1,5(10,5)
f(10,5) = 32 – 15,75
f(10,5) = 16,25
f(15) = 32 – 1,5(15)
f(15) = 32 – 22,5
f(15) = 9,5
f(20) = 32 – 1,5(20)
f(20) = 32 – 30
f(20) = 2
d) Bestimme, wann die Kerze die Höhe 1,8 cm hat.
1,8 = 32 – 1,5x | – 32
–30,2 = –1,5x | : (–1,5)
x = ${\frac{-30,2}{-1,5}}$
x = ${\frac{30,2}{1,5}}$
x = ${\frac{302}{15}}$
x = 20,13 (gerundet auf zwei Nachkommastellen)
e) Ermittle die maximale Brenndauer der Kerze.
0 = 32 – 1,5x | + 1,5x
1,5x = 32 | : 1,5
x = ${\frac{32}{1,5}}$
x = ${\frac{320}{15}}$
x = ${\frac{64}{3}}$
x = 21,33 (gerundet auf zwei Nachkommastellen)