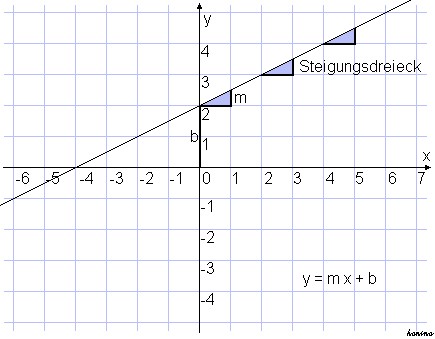
Funktionen sind eindeutige Zuordnungen. Das ist ihr Charakteristikum. Ist das bei einer Funktion der Fall, dass eine eindeutige Zuordnung vorliegt, so kann man in Mathe hierzu einen Funktionsterm aufstellen. Dieser Funktionsterm gibt ganz allgemein die Zuordnung wieder. Man kann solch eine eindeutige Zuordnung jedoch nicht nur algebraisch durch einen Term bestimmen, sondern auch graphisch. Eine Funktion kann schließlich immer auch in ein Koordinatensystem eingezeichnet werden und ihr Verlauf sichtbar gemacht werden. Das nennt man den Graph einer Funktion. Daher kann man auch immer sowohl algebraisch als auch mittels eines Koordinatensystems eindeutig sagen, ob wirklich eine Funktion vorliegt – oder nicht. Es gibt in der Mathematik ja nicht nur Funktionen, das heißt, eindeutige Zuordnungen, sondern auch Relationen, uneindeutige Zuordnungen.
Aufgaben zum Mathe-Stoffgebiet Funktionen
1. Mathematik-Nachhilfe-Aufgabe: Es ist eine Funktion f mit deren Funktionsterm gegeben.
a) f(x) = 3x
b) f(x) = –x + 2
Ermittle die Funktionswerte für: f(5); f(0); f(0,5); f(–0,5); f(–3);

.
Zeichne jeweils den Graph der Funktion. Mache hierzu eine Wertetabelle.
2 Mathe-Nachhilfe-Aufgabe: Eine Wetterstation hat die Temperatur eines ganzen Tages ermittelt und aufgezeichnet. Die ermittelten Daten ergaben folgenden Graphen:
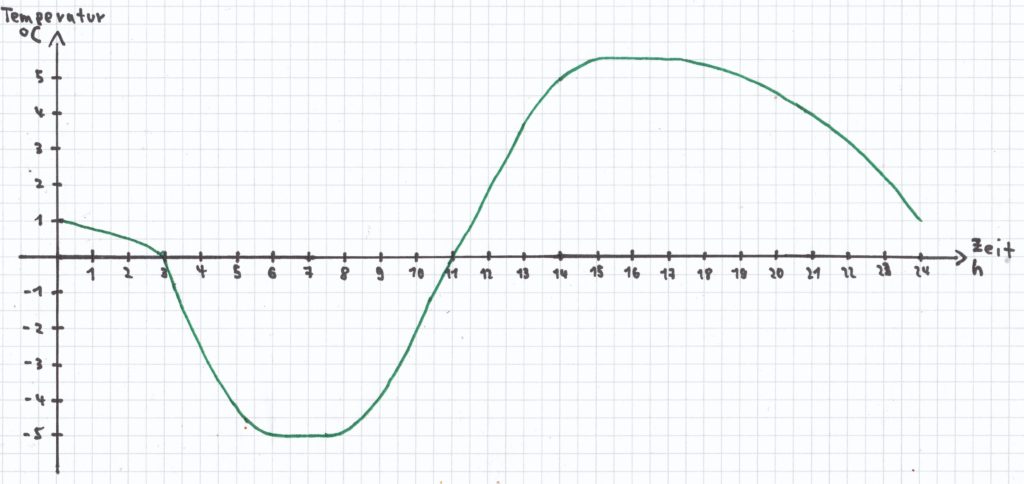
a) Wie viel Grad hatte es an diesem Tag um 0 Uhr, 2 Uhr, 4 Uhr, 6 Uhr … 24 Uhr? Gib die Werte in einer Wertetabelle wieder.
b) Liegt bei der Zuordnung Zeit ↦ Temperatur eine eindeutige Zuordnung vor?
c) Wann ist die Temperatur 2 º C?
d) Liegt bei der Zuordnung Temperatur ${\mapsto}$ Zeit eine eindeutigte Zuordnung vor?
3. Mathematik-Nachhilfe-Aufgabe: Liegt bei der Gleichung eine Funktion vor oder nicht? Setze hierfür für x verschiedene Werte ein und überprüfe, ob eine eindeutige Zuordnung vorliegt.
a)

b)
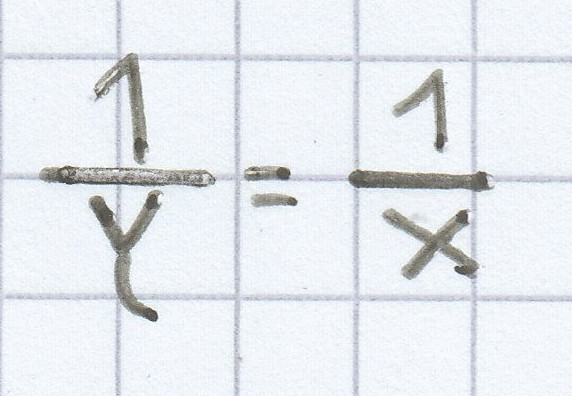
c) |x – y| = 5
d) |x + y| = 0
4. Mathe-Nachhilfe-Aufgabe: Zeichne das Schaubild der Funktion in ein Koordinatensystem ein. Wo ist der x-Wert der Funktion gleich null?
a) y = |x|
b) y = |x| – 4

Lösungen zum Mathe-Stoffgebiet Funktionen
1. Mathematik-Nachhilfe-Aufgabe: Eine Funktion f hat folgende Funktionsterme.
a) f(x) = 3x
b) f(x) = –x + 2
Bestimme die Funktionswerte für: f(5); f(0); f(0,5); f(–0,5); f(–3);

.
Es soll zudem der Graph der Funktion gezeichnet werden. Hierzu soll eine Wertetabelle angefertigt werden.
a) f(x) = 3x
f(5) = 3 · 5
f(5) = 15
f(0) = 3 · 0
f(0) = 0
f(0,5) = 3 · 0,5
f(0,5) = 1,5
f(–0,5) = 3 · (–0,5)
f(–0,5) = –1,5
f(–3) = 3 · (–3)
f(–3) = –9
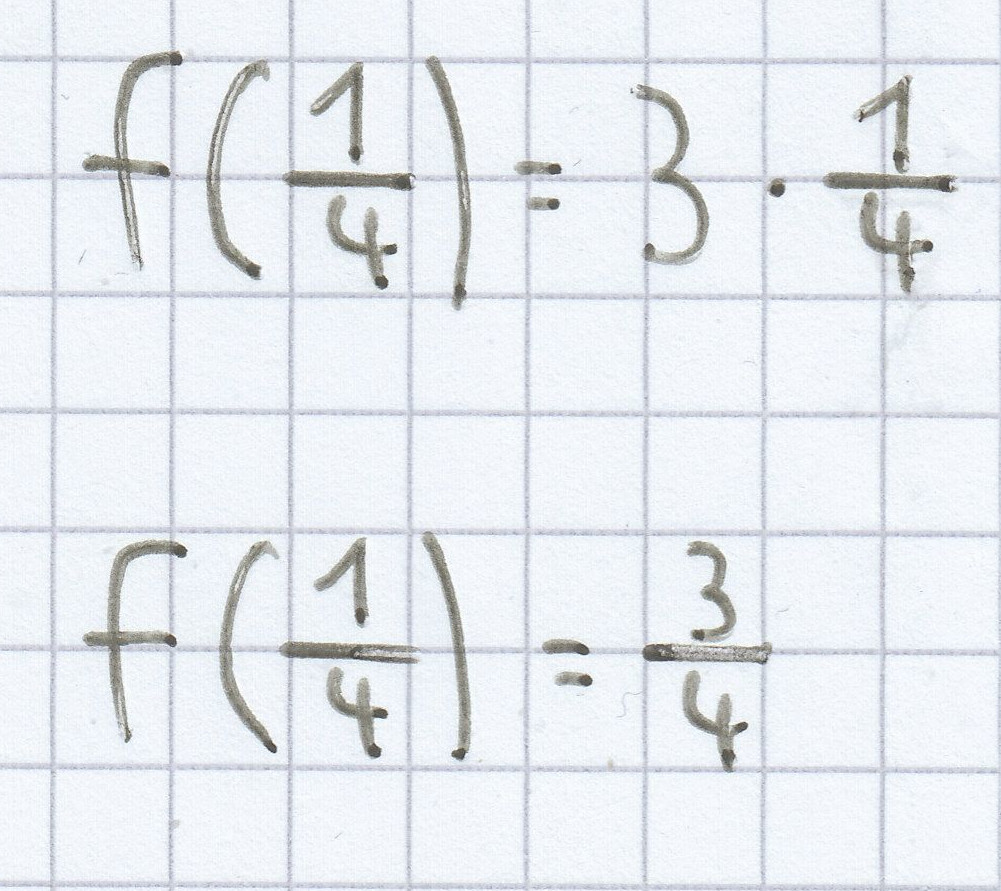
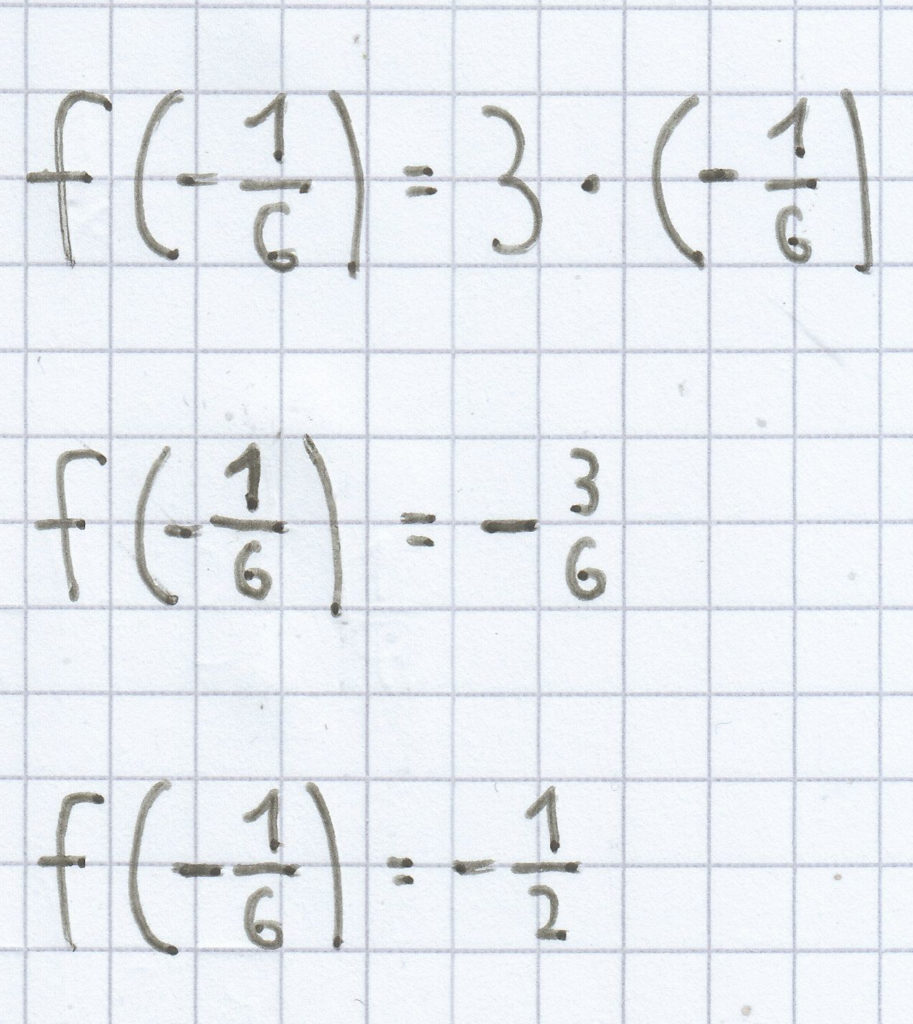
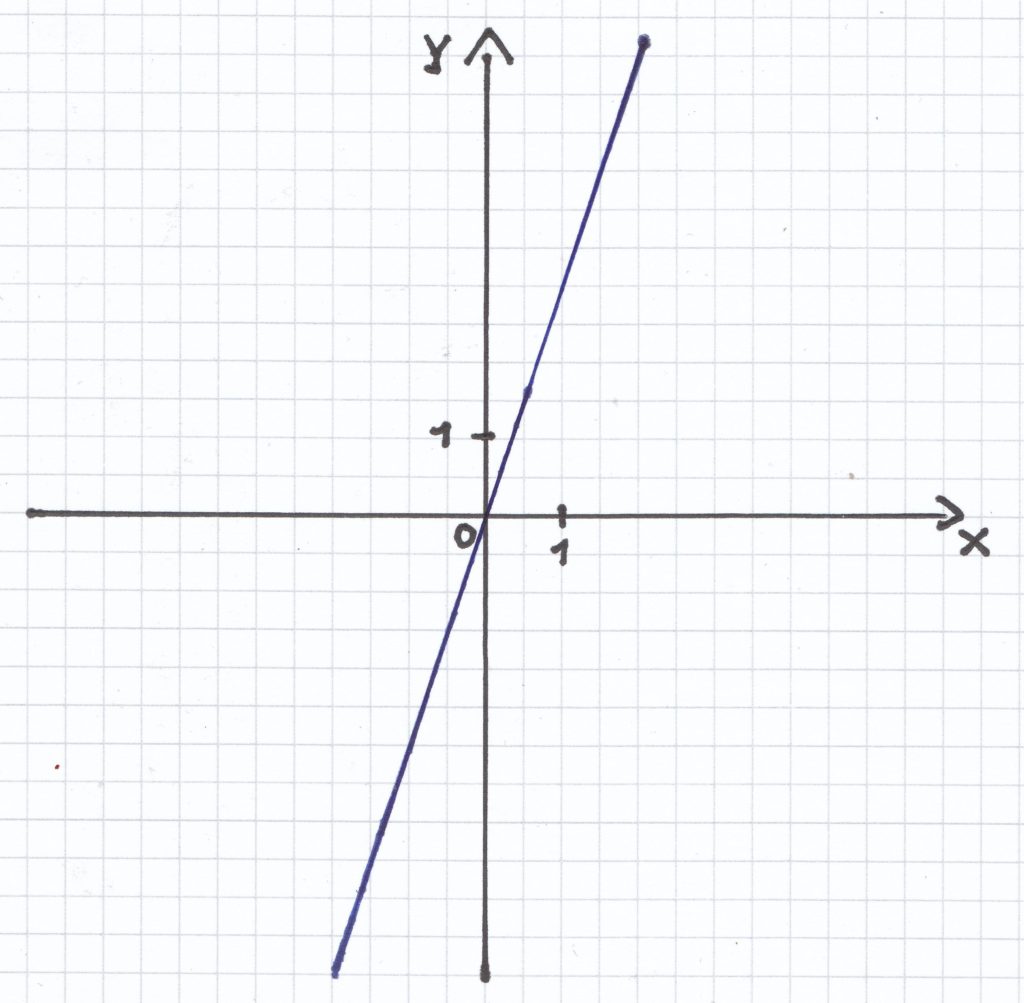
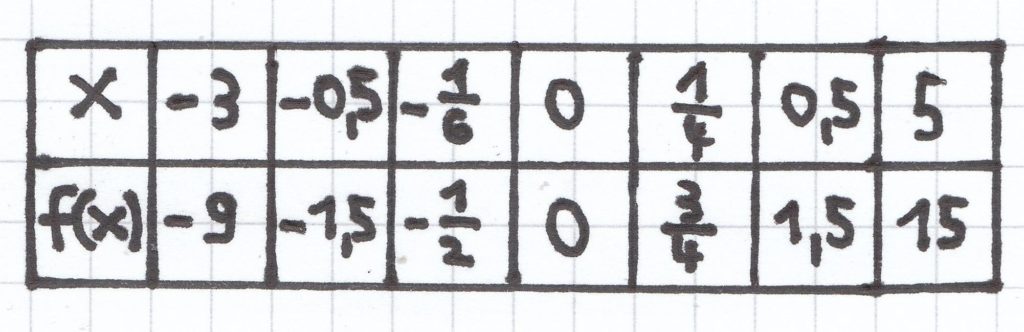
b) f(x) = –x + 2
f(5) = –(5) + 2
f(5) = –3
f(0) = –(0) + 2
f(0) = 2
f(0,5) = –(0,5) + 2
f(0,5) = 1,5
f(–0,5) = –(–0,5) + 2
f(–0,5) = 2,5
f(–3) = –(–3) + 2
f(–3) = 5
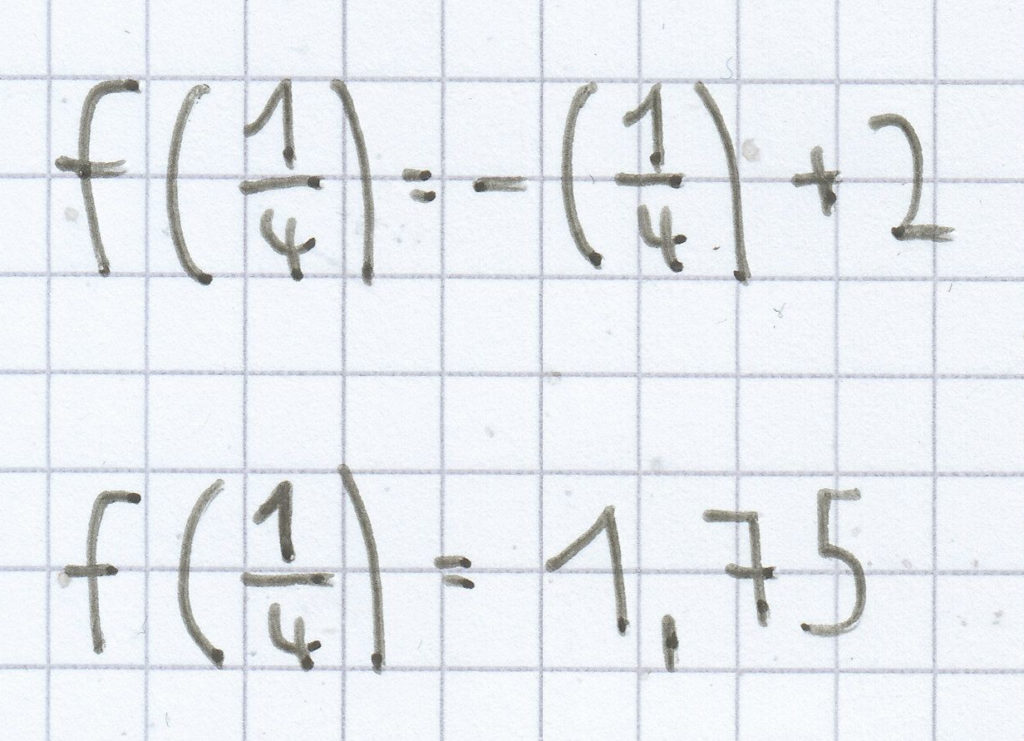

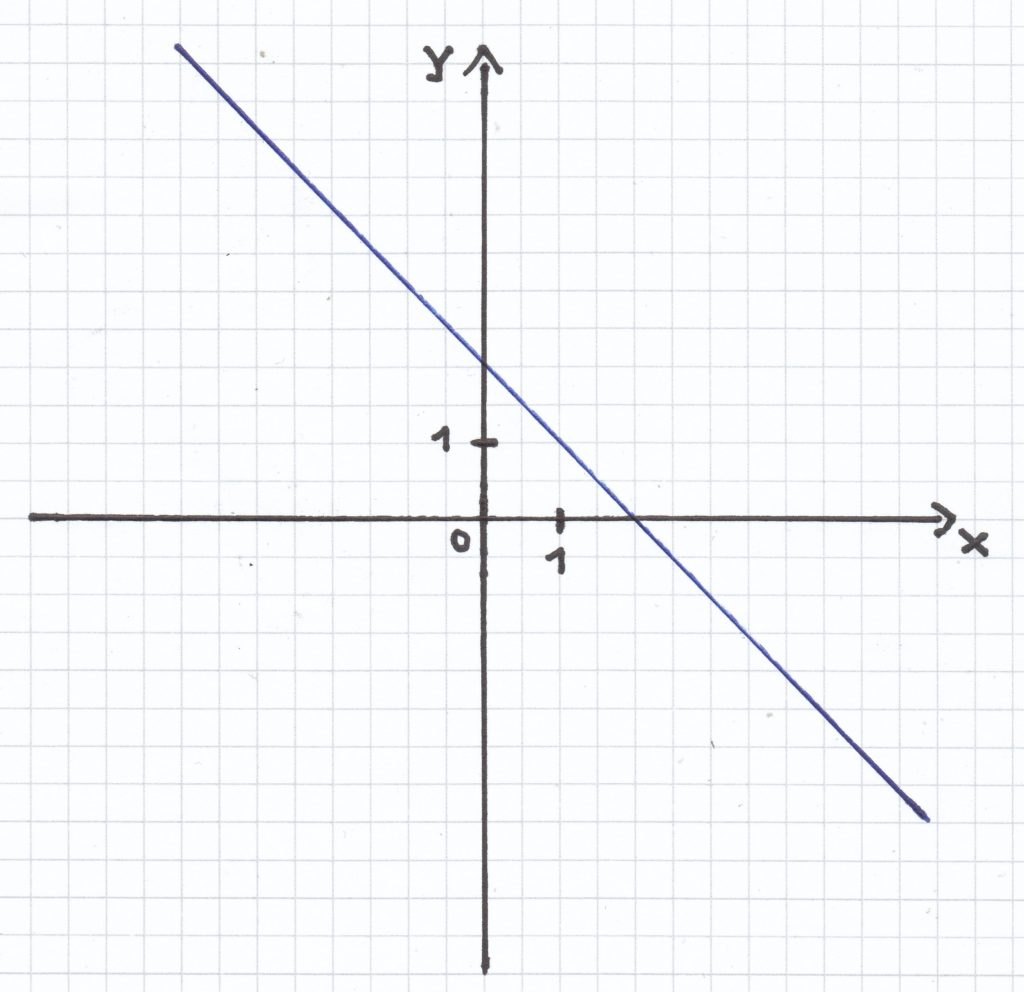

2. Mathe-Nachhilfe-Aufgabe: Die Temperaturen eines ganzen Tages sind von einer Wetterstation ermittelt und aufgezeichnet worden. Der unterstehende Graph ergab sich hieraus:

a) Wie viel Grad hatte es um um 0 Uhr, 2 Uhr, 4 Uhr, 6 Uhr … 24 Uhr an diesem Tag? Lege hierfür eine Wertetabelle an.
Um 0 Uhr hatte es 1 º C;
um 2 Uhr hatte es 0,5 º C;
um 4 Uhr hatte es –2,5 º C;
um 6 Uhr hatte es –5 º C;
um 8 Uhr hatte es ∼ –4,9 º C;
um 10 Uhr hatte es –2 º C;
um 12 Uhr hatte es ∼ 1,75 º C;
um 14 Uhr hatte es 5 º C;
um 16 Uhr hatte es 5,5 º C;
um 18 Uhr hatte es ∼ 5,4 º C;
um 20 Uhr hatte es ∼ 4,6 º C;
um 22 Uhr hatte es ∼ 3,25 º C;

b) Handelt es sich bei der Zuordnung Zeit ↦ Temperatur um eine eindeutige Zuordnung?
Ja, bei der Zuordnung Zeit ↦ Temperatur liegt eine eindeutige Zuordnung vor. Am Graphen kann man für jede Uhrzeit eindeutig eine einzige Temperatur ablesen. Daher ist die Zuordnung absolut eindeutig.
c) Zu welchem Zeitpunkt war die Temperatur 2 º C?
Um 12 Uhr war es 2 º C und ungefähr um 23.15 Uhr.
d) Ist die Zuordnung Temperatur ↦ Zeit eindeutig?
Nein, die Zuordnung Temperatur ↦ Zeit ist nicht eindeutig, da verschiedene Temperaturen an unterschiedlichen Zeiten auftraten. Dadurch ergibt sich eine mehrfache Zuordnung.
3. Mathe-Nachhilfe-Aufgabe: Handelt es sich bei dem Term um eine eindeutige Zuordnung oder nicht? Es sollen hierzu verschiedene Werte von x eingesetzt werden und überprüft werden, ob eine eindeutige Zuordnung vorliegt.
a)
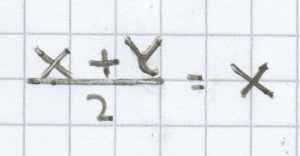
Man kann hier in die Gleichung einfach so Werte einsetzen, dass die Gleichung eine wahre Aussage ergibt. Man kann aber auch die Gleichung, nachdem man den x-Wert eingesetz hat, nach dem y-Wert hin umformen.
x = 2
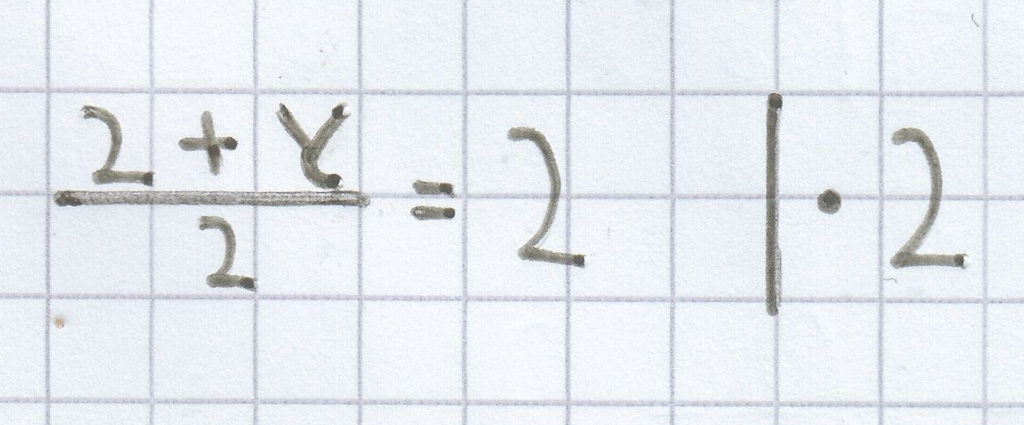
2 + y = 4 | – 2
y = 2
x = 5
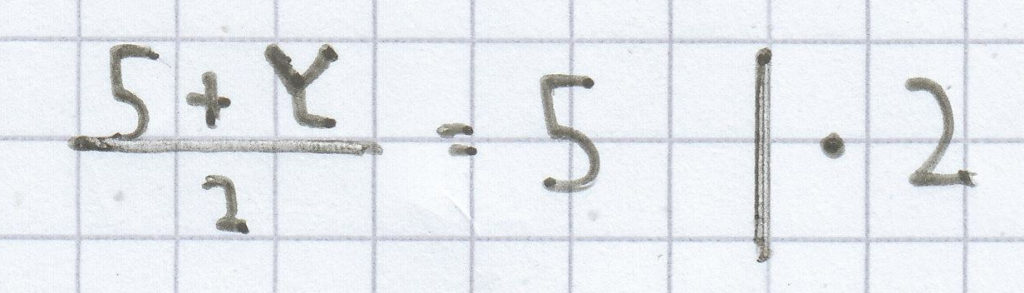
5 + y = 10 | – 5
y = 5
x = 0

y = 0
x = –2
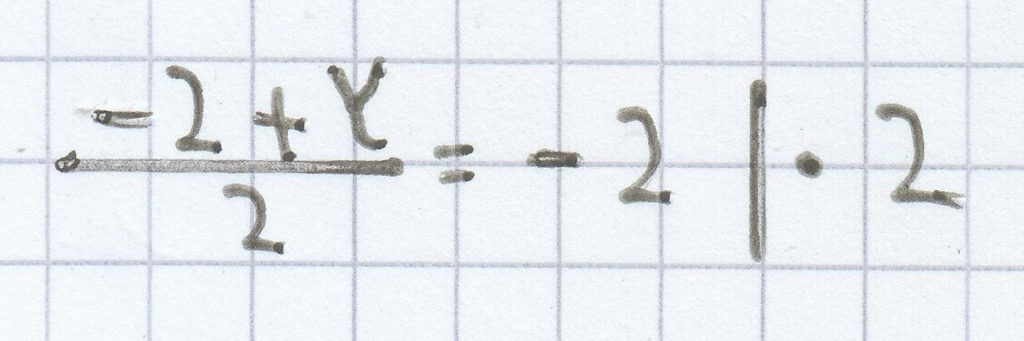
–2 + y = –4 | + 2
y = –2
x = –5

–5 + y = –10 | + 5
y = –5
Hier liegt einen eindeutige Zuordnung vor.
b)
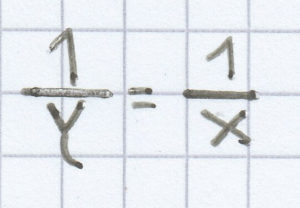
für x, y ≠ 0
x = 2
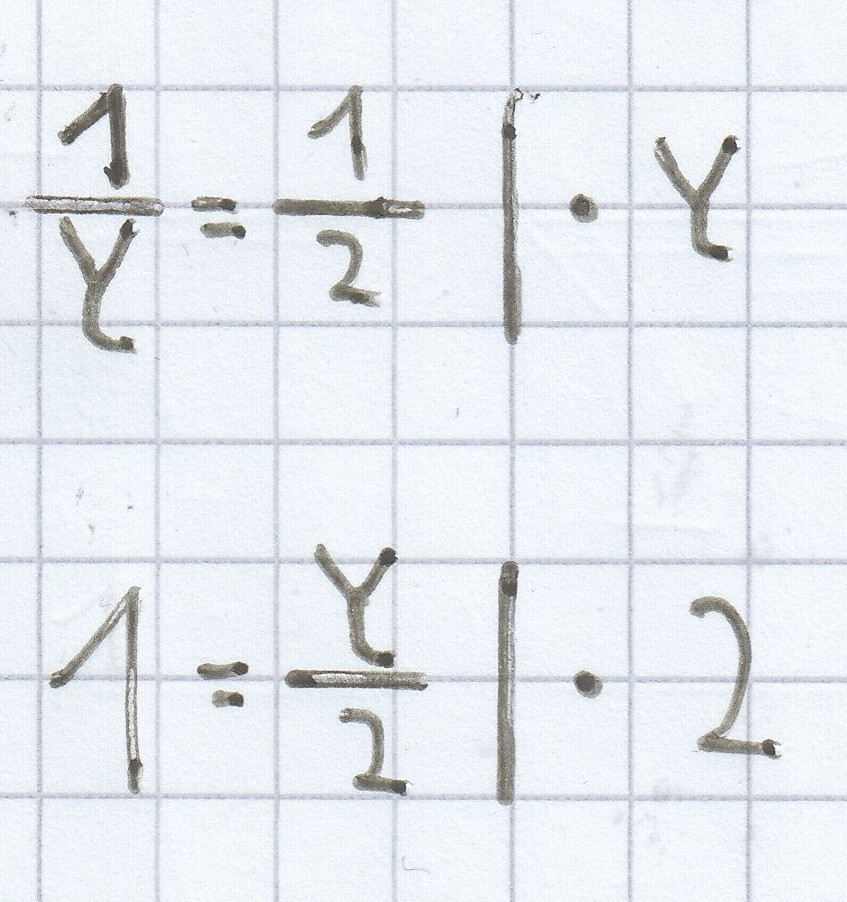
y = 2
x = 5
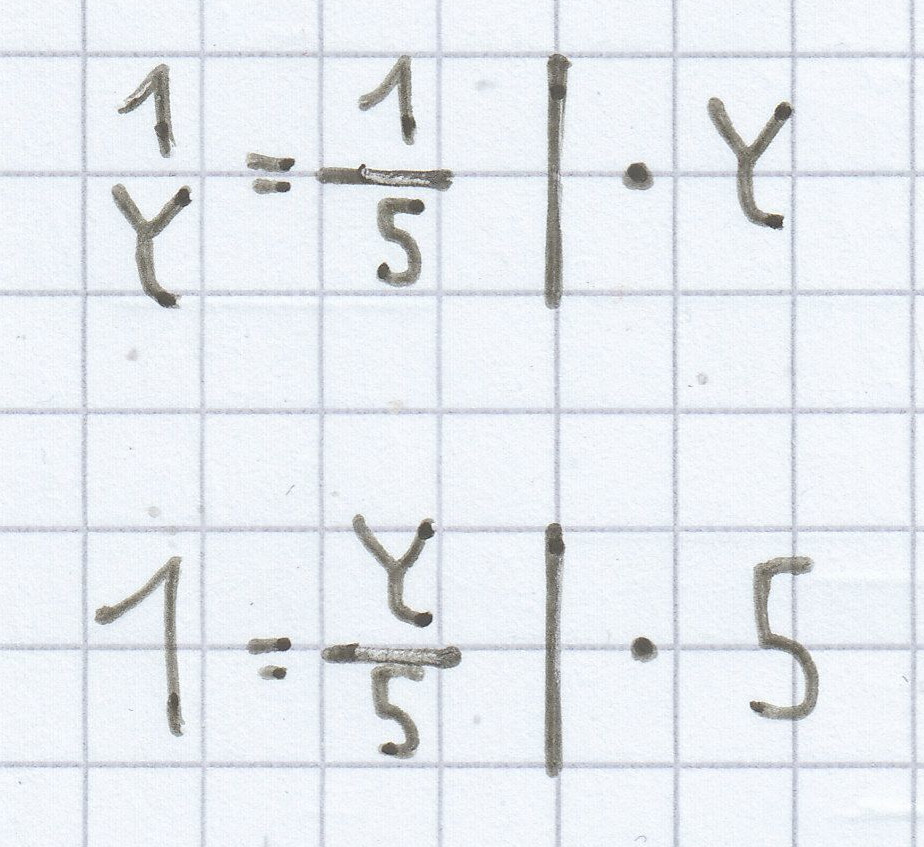
y = 5
x = –2
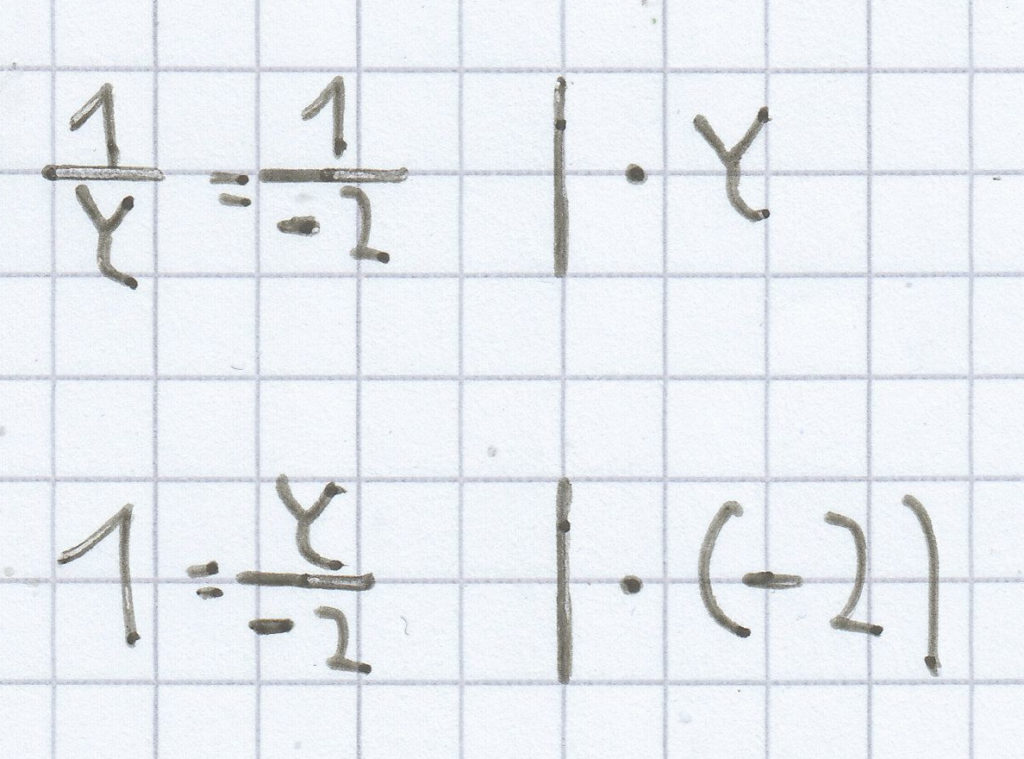
y = –2
x = –5
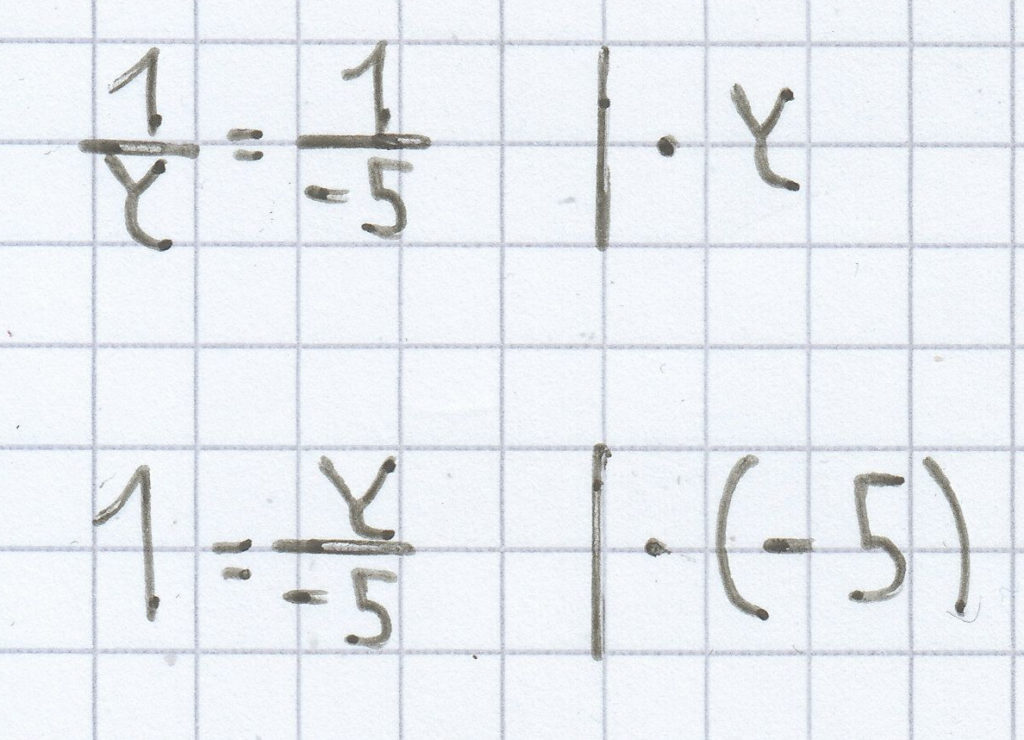
y = –5
Hier handelt es sich ebenso um eine eindeutige Zuordnung.
c) |x – y| = 5
x = 2
|2 – y| = 5
|2 – 7| = 5
|–5| = 5
5 = 5
|2 – (–3)| = 5
|2 + 3| = 5
|5| = 5
5 = 5
Hier zeigt sich bereits bei dem Wert x = 2, dass die Gleichung bei y = 7 und y = –3 eine wahre Aussage liefert. Das genügt bereits, um absolut sagen zu können, dass hier keine eindeutige Zuordnung vorliegt. Bei anderen Werten von x ist das ebenso der Fall, dass zwei y-Werte vorliegen.
x = 5
|5 – y| = 5
|5 – 0| = 5
|5| = 5
5 = 5
|5 – 10| = 5
|–5| = 5
5 = 5
Wie dieses Beispiel ebenso zeigt, kann sich bei x = 5 entweder der y-Wert 0 oder –10 ergeben.
d) |x + y| = 0
x = 2
|2 + y| = 0
|2 + (–2)| = 0
|0| = 0
0 = 0
x = 5
|5 + y| = 0
|5 + (–5)| = 0
|0| = 0
0 = 0
x = 0
|0 + y| = 0
|0 + 0| = 0
|0| = 0
0 = 0
x = –2
|–2 + y| = 0
|–2 + 2| = 0
|0| = 0
0 = 0
x = –5
|–5 + y| = 0
|–5 + 5| = 0
|0| = 0
0 = 0
Hier liegt eine eindeutige Zuordnung vor, da für jeden x-Wert nur ein y-Wert existiert, so dass die Gleichung wahr wird.
4. Mathematik-Nachhilfe-Aufgabe: Der Graph der Funktion soll in ein Koordinatensystem eingezeichnet werden. An welcher Stelle ist der x-Wert gleich null?
a) y = |x|
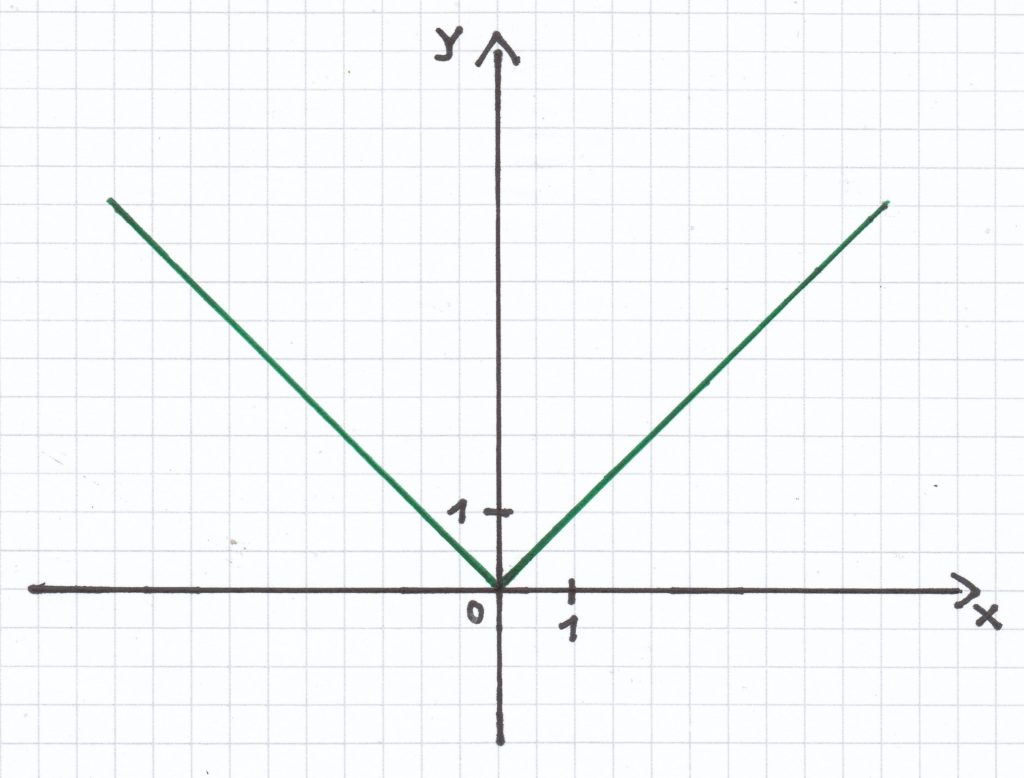
Der x-Wert der Funktion ist an der Stelle x = 0 gleich null.
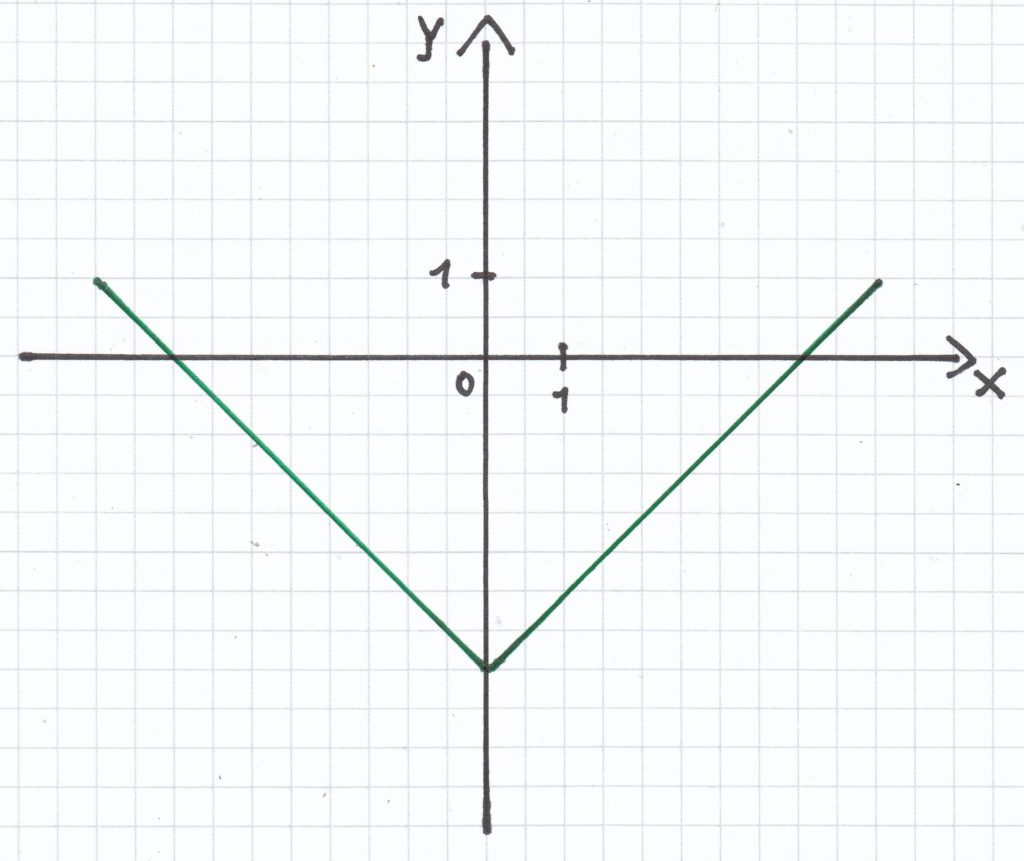
Der x-Wert der Funktion ist an der Stelle x = 4 und x = –4 gleich null.